Quick Look
Grade Level: 11 (9-12)
Time Required: 2 hours
(can be split into two 60-minute sessions)
Expendable Cost/Group: US $2.00
Group Size: 3
Activity Dependency: None
Subject Areas: Chemistry, Measurement, Physical Science, Physics, Problem Solving, Reasoning and Proof, Science and Technology
NGSS Performance Expectations:

| HS-PS3-1 |
Summary
Students use their understanding of projectile physics and fluid dynamics to find the water pressure in water guns. By measuring the range of the water jets, they are able to calculate the theoretical pressure. Students create graphs to analyze how the predicted pressure relates to the number of times they pump the water gun before shooting.
Engineering Connection
When engineers design water amusement park rides, water fountains, or anything that involves shooting water, they use a similar modeling process to determine where water jets will land; this ensures the safety and best experience for its users. More generally, Bernoulli's equation is used by any engineer working with fluids. For example, biomedical engineers use this principle to model the flow and pressure of bodily fluids, and civil engineers use it to determine the size of pipes needed to get water to people's homes and workplaces, or run industrial processes.
Learning Objectives
After this activity, students should be able to:
- Use projectile motion physics to determine the initial velocity of a projectile launched horizontally.
- Use Bernoulli's equation to find the pressure of a fluid.
- Collect, record and analyze data to determine relationships among variables.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-1. Create a computational model to calculate the change in the energy of one component in a system when the change in energy of the other component(s) and energy flows in and out of the system are known. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Create a computational model or simulation of a phenomenon, designed device, process, or system. Alignment agreement: | Energy is a quantitative property of a system that depends on the motion and interactions of matter and radiation within that system. That there is a single quantity called energy is due to the fact that a system's total energy is conserved, even as, within the system, energy is continually transferred from one object to another and between its various possible forms. Alignment agreement: Conservation of energy means that the total change of energy in any system is always equal to the total energy transferred into or out of the system.Alignment agreement: Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Alignment agreement: Mathematical expressions, which quantify how the stored energy in a system depends on its configuration (e.g. relative positions of charged particles, compression of a spring) and how kinetic energy depends on mass and speed, allow the concept of conservation of energy to be used to predict and describe system behavior.Alignment agreement: The availability of energy limits what can occur in any system.Alignment agreement: | Models can be used to predict the behavior of a system, but these predictions have limited precision and reliability due to the assumptions and approximations inherent in models. Alignment agreement: Science assumes the universe is a vast single system in which basic laws are consistent.Alignment agreement: |
Common Core State Standards - Math
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Use appropriate tools strategically.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Energy cannot be created nor destroyed; however, it can be converted from one form to another.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Gather, analyze and interpret data and create graphs regarding position, velocity and acceleration of moving objects
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use direct and indirect evidence to develop and support claims about the conservation of energy in a variety of systems, including transformations to heat
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- water gun with a pumping mechanism (for example, Super Soaker Water Blasters; available at stores such as Target, Kmart, WalMart or online; ~$10 each); ask students to bring in their own, if possible
- moveable desk or table, on which to mount the water gun
- duct tape
- access to a tape measure long enough to measure 35+ feet (11+ meters), the shot distances
- (optional) chalk or tape, to mark off every 10 meters of the shooting range
- pen or pencil
- Take Your Best Shot Worksheet, one per person
- Evaluation & Enhancement Worksheet, one per person
- (optional) Computers and Excel spreadsheet software or MATLAB for data manipulation and graphing
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_bernoulli_lesson01_activity1] to print or download.Pre-Req Knowledge
projectile motion physics, energy conservation, graphing, algebra
Introduction/Motivation
Nothing is better on a hot summer day than the thrill of a fast, steep ride at a water park. To make that ride both fun and safe, engineers must predict how fast people will move, what the forces on their bodies will be, and where they will land. Fortunately for you, projectile motion physics and fluid mechanics provide the equations they need to determine these variables. Today we'll see how.
Procedure
Background
Bernoulli Equation: The Bernoulli equation is an important expression that relates pressure, height and velocity of a fluid at one point along its flow. According to the Venturi Effect, a fluid's pressure decreases as its velocity increases. The Bernoulli equation puts this relationship into mathematical terms and includes a term for fluid height. Think of water moving down a water slide. At the top (where you load), the water is slow moving, pushed only by the water behind it. When the slide drops, the water rushes down quickly, increasing speed as it falls. Thus, the velocity is also affected by gravity through height. When all these terms are related and scaled for density and gravity, we have the Bernoulli equation,
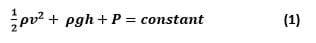
where v is fluid velocity, ρ is fluid density, h is relative height, and P is pressure. Notice the constant has units of pressure as well.
Derived from energy conservation, the Bernoulli equation tells us that the sum of the kinetic and potential energy at any point along a streamline must remain constant. Technically, the equation only applies to the case of flow that is steady (not changing), has constant density, and is inviscid. Many fluids (such as the water in a squirt gun) approximate these conditions, making Bernoulli's equation a useful model.
Finding the Pressure in a Water Gun: Students are asked to use the equations of projectile motion, combined with Bernoulli's equation to find the water pressure. This section explains how to arrive at the solution, if you'd like to give students more guidance. Bernoulli's equation can determine the pressure inside the water gun, but first you have to know how fast the water coming out of it is moving. Kinematics physics equations can help us find the velocity of the water.
As the water leaves the water gun, it is travelling entirely in the horizontal direction, so its total velocity vector can be reduced to horizontal velocity, or Vx . A simple relationship relates the horizontal velocity (V x) to the distance (x) it travels in a certain amount of time (t),

The distance can be measured, but unfortunately, we do not know time. However, we can determine the time using another kinematic equation that relates time to the initial and final vertical positions of the water (y0 and yf ), the initial vertical velocity (vy0 ), and the vertical acceleration, ay ,
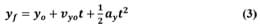
This equation simplifies greatly under the initial conditions set by this problem. The initial vertical position of the water (y0 ) is the table, and the final position (yf ) is the floor, so yf– y0 is simply the height of the table, or h. As we already said, the initial velocity of the water is directed horizontally, making the initial vertical velocity, vy0 , equal to zero as well. Finally, the vertical acceleration is g, or -9.8 m/s2, the constant acceleration due to gravity. The equation simplifies to

Using algebra, we can solve for time, and then plug the result into Equation 2 to solve for velocity.
Once velocity is found, we can solve for pressure using Bernoulli's equation. Because the Bernoulli equation equals the same constant at all points along a streamline, we can set the Bernoulli equation at two points equal to each other and use information on the system at one point to solve for information at another, as shown in the equation below:
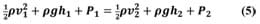
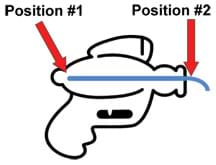
For this particular problem, two useful points to choose are the inside of the gun (position #1) and the outside of the gun at the nozzle (position #2). These points are chosen because we know some of the quantities at these locations. We know that the velocity of the water inside the gun (v1 ) is initially zero, and that the pressure outside the gun (P2 ) is the atmospheric pressure. The density (ρ) is the density of water, and the relative heights (h1 and h2 ) are equal because we are keeping the gun level. After some algebraic manipulation, the pressure inside the water gun is easily solvable.
Before the Activity
- Gather materials. If possible, ask students to bring their own super soaker water guns from home.
- Make copies of the Take Your Best Shot Worksheet and the Evaluation & Enhancement Worksheet.
- Find an appropriate location to shoot the squirt guns. It is best to secure a relatively open space with access to water and a dry concrete surface (to better see where water lands).
- Set up a table or desk so it is level, and mark off with chalk or tape the distance from the table every meter for ~10 meters.

With the Students
- Conduct a pre-activity assessment discussion with the students, as described in the Assessment section.
- Have students read the background and procedural instructions on the Take Your Best Shot Worksheet, and set up their experiments.
- When ready, run the experiments as described in the worksheet.
- Have the students perform the calculations and graphing on the Take Your Best Shot Worksheet. (Optional: Have them use the digital spreadsheet, Take Your Best Shot Worksheet Excel Code or Take Your Best Shot Worksheet MATLAB for help with data manipulation and graphing.
- Have students complete the Evaluation & Enhancement Worksheet.
Vocabulary/Definitions
incompressible: A fluid that does not compress, or in other words it has a constant density.
inviscid: Effects from the viscosity of a fluid are ignored.
range: Horizontal distance traveled by a projectile.
streamline: A line tangent to the direction of flow in a fluid that illustrates how fluid flows around an obstacle.
viscosity: The internal friction in a fluid. Fluids with high viscosity are thick and slow (such as molasses), while those with low viscosity (such as alcohol) are thin and fast.
Assessment
Pre-Activity Assessment
Discussion: Solicit, integrate and summarize student responses.
- Most popular water guns today use a hand pump to build up air pressure and shoot water out of a tube, often in order to soak your friends and family while looking totally awesome. How much pressure do you think it takes to have this fun? How would one even go about calculating that? The following activity answers those questions, but first, what do you think?
Activity Embedded Assessment
Activity Worksheet: Have students individually complete the Take Your Best Shot Worksheet. Review their answers to gauge their mastery of the subject.
Post-Activity Assessment
Evaluation & Enhancement Worksheet: Have students individually complete the Evaluation & Enhancement Worksheet in which they reflect upon potential sources for error in the experiment, their impact on the results, their graph shapes, and how the data could help them in real-world problem solving. Review their answers to gauge their mastery of the subject.
Safety Issues
- Do not aim squirt guns at eyes.
Troubleshooting Tips
Depending on your exact water gun design, it is probably best to place the water gun sideways on a flat table to ensure a horizontal shot and easy trigger access.
One or two pumps might not yield any results depending on the type of water gun used. If this is the case, have students start their data collection at the first number of pumps that yield results and perform trials at up to ten pumps beyond that.
It is important to leave some air in the water tank to make sure the water gun works properly.
If holding the trigger until the water stops shooting does not work, the depressurization of the chamber between trials can be achieved by opening the water tank, thereby depressurizing the system.
If students have trouble with manipulating the data themselves, see the attached Excel and MATLAB coding files to guide students through the process.
Activity Scaling
- For lower grades, have students calculate and graph the pressure generated by five pumps instead of 10. Also, depending on students' math ability, provide them with more help in doing the calculations. For instance, provide the equations in order of use and rearrange each one so that the unknowns are on the left sides, requiring minimal algebraic manipulation.
- For higher grades, have students work out the problem solution more independently and require more analysis of the results.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to Pascal's law, Archimedes' principle and Bernoulli's principle. Fundamental definitions, equations, practice problems and engineering applications are supplied.

Students learn about the relationships between the components of the Bernoulli equation through real-life engineering examples and practice problems.
References
Bernoulli's principle. Last updated November 2, 2009. Wikipedia, The Free Encyclopedia. 2 Nov Accessed November 7, 2009. http://en.wikipedia.org/wiki/Bernoulli%27s_principle
Knight, Randall. Physics for Scientists and Engineers: A Strategic Approach. Second edition. San Francisco, CA: Pearson Addison-Wesley, 2008.
Munson, B. R., Young, D.F., Okiishi, T.H., Fundamentals of Fluid Mechanics. Fifth edition. New York, NY: John Wiley & Sons, Inc., 2006.
Copyright
© 2009 by Regents of the University of Colorado.Contributors
James Prager; Karen King; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: December 12, 2020






User Comments & Tips