Quick Look
Grade Level: 9 (9-12)
Time Required: 45 minutes
This activity uses some non-expendable (reusable) items, such as Cartesian divers; see the Materials List for details, including a homemade alternative.
Expendable Cost/Group: US $0.00 This activity uses some non-expendable (reusable) items, such as Cartesian divers; see the Materials List for details, including a homemade alternative.
Group Size: 28
Activity Dependency: None
Subject Areas: Chemistry, Physical Science, Physics, Problem Solving, Reasoning and Proof
NGSS Performance Expectations:

| HS-ESS2-5 |
Summary
Students observe Pascal's law, Archimedes' principle and the ideal gas law as a Cartesian diver moves within a closed system. The Cartesian diver is neutrally buoyant and begins to sink when an external pressure is applied to the closed system. A basic explanation and proof of this process is provided in this activity, and supplementary ideas for more extensive demonstrations and independent group activities are presented.
Engineering Connection
The concepts of Pascal's law, Archimedes' principle, the ideal gas law and the density-buoyancy relationship are important in science, engineering and technology applications such as fish physiology, scuba diving and various submersibles. Most boney fish have a swim bladder that enables them to control their buoyancy, or height in the water column, without swimming. Scuba divers use special equipment such as weighting systems, diving suits and buoyancy compensators to control their buoyancy. Submersibles enable the exploration of depths much greater than can be reached via satellite and shipboard technologies; these creative submersible and remotely operated vehicle (ROV) inventions are necessary for researchers to explore very deep ocean communities and discover new species.
Learning Objectives
After this activity, students should be able to:
- Use a Cartesian diver and interpret how it works by using terminology such as density, buoyancy and pressure.
- Explain the physics of the Cartesian diver behavior based on an understanding of Pascal's law and Archimedes' principle.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Asking questions and defining problems in grades 9–12 builds from grades K–8 experiences and progresses to formulating, refining, and evaluating empirically testable questions and design problems using models and simulations.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ESS2-5. Plan and conduct an investigation of the properties of water and its effects on Earth materials and surface processes. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan and conduct an investigation individually and collaboratively to produce data to serve as the basis for evidence, and in the design: decide on types, how much, and accuracy of data needed to produce reliable measurements and consider limitations on the precision of the data (e.g., number of trials, cost, risk, time), and refine the design accordingly. Alignment agreement: | The abundance of liquid water on Earth's surface and its unique combination of physical and chemical properties are central to the planet's dynamics. These properties include water's exceptional capacity to absorb, store, and release large amounts of energy, transmit sunlight, expand upon freezing, dissolve and transport materials, and lower the viscosities and melting points of rocks. Alignment agreement: | The functions and properties of natural and designed objects and systems can be inferred from their overall structure, the way their components are shaped and used, and the molecular substructures of its various materials. Alignment agreement: |
Common Core State Standards - Math
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Assess how similarities and differences among scientific, mathematical, engineering, and technological knowledge and skills contributed to the design of a product or system.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Texas - Science
-
know that scientific theories are based on natural and physical phenomena and are capable of being tested by multiple independent researchers. Unlike hypotheses, scientific theories are well-established and highly-reliable explanations, but may be subject to change as new areas of science and new technologies are developed;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
express and interpret relationships symbolically in accordance with accepted theories to make predictions and solve problems mathematically, including problems requiring proportional reasoning and graphical vector addition.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Science concepts. The student understands the principles of ideal gas behavior, kinetic molecular theory, and the conditions that influence the behavior of gases. The student is expected to:
(Grades
10 -
12)
More Details
Do you agree with this alignment?
Materials List
This activity is presented as a class activity using one Cartesian diver setup, but it can easily be expanded with more materials so that groups of four students or individual students each have an activity setup.
To perform this activity as a class, the following materials are needed:
- 1-liter clear plastic soda bottle with cap, filled with water (soda bottle costs ~$2 or free in recycling bin)
- bowl of water
- Cartesian diver, available at science teaching supply stores, such as the pre-made single Cartesian diver shaped like a squid (#P1-2000) for $2.95 from Arbor Scientific at https://www.arborsci.com/products/single-cartesian-diver
- meter sticks, or other way to measure the classroom dimensions in metric units
- Cartesian Diver Worksheet, one per student
- (optional) if experiencing trouble with squeezing, or to conduct the "Trained Divers" activity extension, use a pressurizing pump to pressurize the 1-liter bottle, such as the individual pressure pumper (#P1-2050) for $3.25 from Arbor Scientific at https://www.arborsci.com/products/individual-pressure-pumper
To have students/groups make their own Cartesian diver setups, each needs:
- 1-liter clear plastic soda bottle with cap, filled with water
- bowl of water
- Cartesian diver, available at science teaching supply stores, such as the pre-made squid-shaped diver described above, or the do-it-yourself super diver kit (#P1-2000-01) with plastic pipettes and other parts and instructions (and a pressure pumper) to make 30 divers from Arbor Scientific at https://www.arborsci.com/products/super-diver-kit; alternatively, obtain your own parts, such as plastic pipettes and weights (nuts, wire), or condiment packets (see below) to make as many divers as you want
How to construct your own Cartesian diver(s) from pipettes, nuts and wire:
- Cut a plastic pipette so that the length of the tube protruding from the bulb is about 1 inch long.
- Place the metal nut around the tube, or wrap some metal wire around the tube to act as a weight.
How to prepare your own condiment packet Cartesian diver(s):
- Ask students to bring to class, or obtain at restaurants or cafeterias, various small plastic condiment packets, such as those for ketchup, mustard, mayonnaise, soy sauce, plum sauce, etc.
- The best Cartesian divers are neutrally buoyant so test the packets in a bowl of water to observe their buoyancy in order to determine which work best as trustworthy divers.
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/uoh_fluidmechanics_lesson01_activity1] to print or download.Pre-Req Knowledge
Students should have a basic understanding of Pascal's law, Archimedes' principle, the relationship between mass, volume and density, and the ideal gas law. Refer to the Archimedes' Principle, Pascal's Law and Bernoulli's Principle associated lesson for information on these topics.
Introduction/Motivation
Who wants to take a guess at how much the air in this classroom weighs? (Listen to a few student answers and then move on.) To calculate how much the air in this classroom weighs, we need to determine a few things. Who knows what information we need in order to begin? (Listen to student answers until all correct answers have been stated. Write the correct answers on the classroom board.) That's right, we need to know the volume of the classroom—that means we need to know its length, width and height measurements. What else? That's right, we need to know the density of air at room temperature.
Who will volunteer to measure the length, width and height of the classroom? (Choose three to six volunteers to measure the classroom dimensions in metric units.) Who wants to volunteer to calculate on the board how much the air weighs? (Choose a volunteer to work the problem on the board. Draw on the board a table titled, "Densities of Various Gases" and include any gases you wish, such as the Table 1 example.)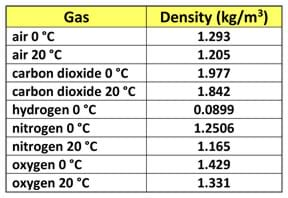
(An example calculation using L = 15.85 m, W = 13.4 m and H = 3.66 m as classroom dimensions results in the following volume, mass and weight:
volume (V) = L * W * H = (15.85 m) * (13.4 m) * (3.66 m ) = 777.35 m3
mass (M) = V * density (ρ) = (777.35 m3) * (1.205 kg/m3) = 936.71 kg
weight (W) = M * gravity (g) = (936.71 kg) (9.81 m/s2) = 9189.09 N ~ 2,000 pounds!)
(Verify the student's calculations because the weight of air in each classroom will be different than the example calculation provided because it depends on the room size. Ask students what they think about the weight of the air in the room.) Who remembers the relationship between mass and volume? (Listen to student answers and guide them into a conversation about the air in the classroom and the density relationship.)
Now that we know how much the air around us weighs, imagine how much the water around a scuba diver weighs! What do scuba divers have to help control the pressure from the surrounding water? Think about Archimedes' principle and buoyancy. What do scuba divers have that controls their buoyancy? (Expected possible answers: Scuba divers use weighting systems, diving suits and buoyancy compensators to control buoyancy.)
What are some examples of engineered devices that can dive deeper than scuba divers? (Expected possible answers: Submarines and remote operated vehicles (ROVs or "robots"). How are they able to dive deeper than scuba divers? (Answer: They are designed to withstand higher pressures.) What are submarines and ROVs used for and why are they important? (Possible answers: They are essential to helping us investigate deep-water regions that humans are unable to survive; they can reach depths much greater than satellite and shipboard technologies; they enable exploration of abysmal ocean communities and the discovery of new species.)
Who has heard of a Cartesian diver? (Listen to student answers.) The Cartesian diver is named after the French philosopher, mathematician and scientist René Descartes who lived 1596–1650. It is interesting that the Cartesian diver is named after Descartes, when in fact it was Galileo's student Raffaelo Maggiotti who discovered the Cartesian diver, which he initially named the "Cartesian Devil." The French refer to the Cartesian diver as "ludion," which means actor, jester or wandering entertainer. Does anyone know what quotation Descartes is famous for saying? (See if any students know. Then write the correct answer on the board: "I think, therefore I am.") Thinking about the definition for "ludion," many people suggest that the Cartesian diver is named after Descartes because it makes you think! Who would have known?
Procedure
Background
Pascal's law states that a pressure applied anywhere to a fluid causes a force to be transmitted equally in all directions; a change in pressure disperses equally throughout the fluid; and a force acts at right angles to any surface in contact with the fluid.
When a bottle containing water and a Cartesian diver is pressurized (squeezed), the pressure within the entire bottle and Cartesian diver is increased. Archimedes' principle states that the buoyant force is equal to the weight of the water displaced; therefore, an object sinks if the weight of the water displaced weighs less than the object, or the object floats if the weight of the water displaced weighs more than the object. The Cartesian diver sinks because density is increased when water is taken up into the pipette of the Cartesian diver and the volume of air decreases.
Before the Activity
- Decide whether you will use a pre-made Cartesian diver or make your own from a kit, your own parts, or condiment packets. Then gather all materials and construct and test the Cartesian diver.
- Make copies of the Cartesian Diver Worksheet, one per student.
With the Students
- Present the Introduction/Motivation content to the class.
- (optional) Write the vocabulary words and definitions on the classroom board. Alternatively, save them for later, as part of the worksheet assessment.
- Fill the one-liter plastic bottle with room-temperature water.
- Show students the Cartesian diver and what it is made of. If a pre-made Cartesian diver is used, it may be difficult for students to see the pipette under the rubber squid. If a homemade Cartesian diver is used, one constructed by the instructor or students, verify that each student understands what materials were used to construct it (pipette, weight, etc.). Skip this step if using condiment packets. Answer any questions students may have.
- Squeeze the pipette portion of the Cartesian diver to expel the air and submerge the Cartesian diver in a bowl of water so the pipette can take in water. Adjust the amount of water inside the pipette until it is neutrally buoyant—neither floating nor sinking. Alternative: If conducting this activity with condiment packets, have students place the packets into a bowl of water and observe them to determine which are neutrally buoyant. Select the most neutrally buoyant condiment packets and proceed.
- Place the prepared Cartesian diver inside the one-liter bottle and make sure that the bottle is completely filled with water.
- Screw the cap on the bottle so it is closed securely (see Figure 1-left).
- Predictions: Ask students to guess what will happen when you squeeze the bottle. Ask students use scientific terminology for their answers and explanations.

Figure 1. (left) A Cartesian diver demonstration setup with no pressure applied. (right) A sunken Cartesian diver with an applied external pressure (right). - While holding up the bottle so all students can see it, squeeze the bottle (see Figure 1-right). As necessary, do this a few times, so that students have adequate time to observe what happens.
- Hand out worksheets and direct students to answer the questions, including scientifically explaining what has happened using the laws of physics they learned in the associated lesson.
- Have students complete the worksheets and turn them in for grading. The next day, review the answers in a class discussion in order to clarify any misconceptions and reinforce answers for everyone's benefit.
Vocabulary/Definitions
buoyancy: The ability of an object to float in a liquid.
density: A measurement of the compactness of an object.
mass: A measurement of the amount of matter in an object.
mass density: Mass per unit volume of a substance.
pressure: A measurement of force per unit area.
volume: A measurement of the amount of space an object occupies.
Assessment
Pre-Activity Assessment
Weight of Classroom Air: Ask students to calculate how much the air in the classroom weighs. This exercise helps students observe the relationship between weight and the amount of space it occupies. The goal is to get students to think about squeezing or expanding the same amount of air into a different size classroom (changing volume) to help them make the connection between volume and density.
Activity Embedded Assessment
Predictions: Ask students what they think will happen when the one-liter bottle is squeezed. Guide them to use terminology and theory learned in the associated lesson to provide scientific explanations for their hypotheses. Note: If the bottle is turned upside down, ask students to explain why the Cartesian diver no longer works. When the bottle is upside down, the air inside the Cartesian diver is released and replaced with water, causing the diver to become denser and sink.
Post-Activity Assessment
Worksheet or Quiz: Assign students to complete the Cartesian Diver Worksheet in class or as homework. The worksheet encompasses definitions to help students start thinking about what these terms mean and the science behind the theories presented in class, a re-cap of the procedure, and a series of questions that guides them (even those who may be stumped!) to understanding the theory behind the Cartesian diver. As a bonus question, students are asked to make engineering connections and give examples of how these principles are used in science, engineering and/or technology. Some examples are a Galileo thermometer, high-pressure systems like autoclaves (laboratory instrument that sanitizes lab equipment), deep sea drilling, etc. Have students hand in the worksheets for grading; review their answers to gauge their depth of comprehension. The next day, review the answers as a class to clarify any misconceptions and reinforce answers for everyone's benefit. Alternatively: Modify the worksheet into a quiz by removing the objectives and procedure sections.
Troubleshooting Tips
Make sure the one-liter bottle is filled with water to the very top.
Use room temperature water because hotter or colder water affects the pressure in the bottle and the water level in the diver.
If the diver sinks on its own over time, it could be due to temperature and pressure changes. Open the bottle and replace the cap or unscrew the cap slightly and squeeze the bottle so a little bit of water is removed and a partial vacuum is created. If neither of these adjustments solves the problem, remove the Cartesian diver and re-adjust the water inside the diver.
If the bottle is turned upside down, the Cartesian diver fills with water and become denser and sinks. If this happens, remove the Cartesian diver and re-adjust its internal water/air ratio.
If a pre-made rubber Cartesian diver is used, do not leave it in the water for extended periods of time because it deteriorates.
Activity Extensions
Trained Divers: Label five Cartesian divers 1–5 and adjust the water inside of the five divers so that they are all neutrally buoyant. Remove 5 drops of water from diver #2, 10 drops of water from diver #3, 15 drops of water from diver #4, and 20 drops of water from diver #5. You can adjust the number of drops of water removed as long as diver #1 has the most water and diver #5 has the least. Place all five divers in the one-liter bottle and squeeze the bottle so that the divers sink at different times. If you are unable to squeeze hard enough to sink the last few divers, use a pressurizing pump. Tell students that you have "trained" the divers, but then guide them to investigate until they conclude that each diver has a different water/air ration inside.
Hook and Sinker: Wrap a wire around a Cartesian diver and intentionally sink the diver so that it is resting on the bottom of a one-liter bottle; this diver is called the "Sinker." Attach a wire to a second Cartesian diver so that is neutrally buoyant and place it in the one-liter bottle; this diver is called the "Hook." Let students try to hook the Sinker by squeezing the bottle and tilting it sideways, while never letting the bottle be turned upside down. Make an engineering connection by referring to the Hook as a submersible whose task is to collect samples (the Sinker) from the ocean bottom for researchers to analyze in the laboratory.
Activity Scaling
For a more challenging activity:
- Challenge students to make the Cartesian divers sink without opening the bottle. In this case, do not conduct the above activity or tell them to squeeze the bottle. Let them figure it out.
- Give students materials and challenge them to design their own Cartesian divers. In this case, do not conduct the above activity or tell them how to construct the diver. Let them figure something out.
Additional Multimedia Support
It is helpful for the instructor to watch a 2:52-minute video called Soda Bottle Diver –Cartesian Diver, to gain a familiarity with the materials used in this activity; view this Steve Spangler science experiment at https://www.youtube.com/watch?v=sNOXFiJ4IDU.
The Wikipedia entry for Cartesian diver includes links to two video demonstrations (14 seconds and 30 seconds); see http://en.wikipedia.org/wiki/Cartesian_diver.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to Pascal's law, Archimedes' principle and Bernoulli's principle. Fundamental definitions, equations, practice problems and engineering applications are supplied.

Students learn about the fundamental concepts important to fluid power, which includes both pneumatic (gas) and hydraulic (liquid) systems.
References
Gases – Densities. The Engineering ToolBox. Accessed January 3, 2014. (Source for Table 1 densities of some common gases) http://www.engineeringtoolbox.com/gas-density-d_158.html
Hewitt, Paul. Conceptual Physics Fundamentals. San Francisco, CA: Pearson Addison Wesley, 2009.
Copyright
© 2014 by Regents of the University of Colorado; original © 2013 University of HoustonContributors
Emily Sappington, Mila TaylorSupporting Program
National Science Foundation GK-12 and Research Experience for Teachers (RET) Programs, University of HoustonAcknowledgements
This digital library content was developed by the University of Houston's College of Engineering, based upon work supported by the National Science Foundation under GK-12 grant no. DGE 0840889. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Last modified: March 7, 2020






User Comments & Tips