Quick Look
Grade Level: 11 (9-12)
Time Required: 30 minutes
Lesson Dependency: None
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| HS-PS3-1 |

Summary
Bernoulli's principle relates the pressure of a fluid to its elevation and its speed. Bernoulli's equation can be used to approximate these parameters in water, air or any fluid that has very low viscosity. Students use the associated activity to learn about the relationships between the components of the Bernoulli equation through real-life engineering examples and practice problems.Engineering Connection
The Bernoulli principle has a wide range of applications in engineering fluid dynamics, from aerospace wing design to designing pipes for hydroelectric plants. For example, in the case of a hydroelectric plant that utilizes water flow from mountain reservoir, knowing the elevation change from the reservoir in the mountains to the plant in town helps engineers determine how fast the water will be flowing through the energy-generating turbines in the plant.
Learning Objectives
After this lesson, students should be able to:
- Calculate an unknown fluid condition (for example, fluid pressure, velocity, density or height) at one point along a flow streamline, if conditions are known at another point along the same streamline.
- Use the Bernoulli equation to explain that faster airflow causes a decrease in pressure, and give an example of a real-life application.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-1. Create a computational model to calculate the change in the energy of one component in a system when the change in energy of the other component(s) and energy flows in and out of the system are known. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Create a computational model or simulation of a phenomenon, designed device, process, or system. Alignment agreement: Use mathematical representations of phenomena to describe explanations.Alignment agreement: | Energy is a quantitative property of a system that depends on the motion and interactions of matter and radiation within that system. That there is a single quantity called energy is due to the fact that a system's total energy is conserved, even as, within the system, energy is continually transferred from one object to another and between its various possible forms. Alignment agreement: Conservation of energy means that the total change of energy in any system is always equal to the total energy transferred into or out of the system.Alignment agreement: Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Alignment agreement: Mathematical expressions, which quantify how the stored energy in a system depends on its configuration (e.g. relative positions of charged particles, compression of a spring) and how kinetic energy depends on mass and speed, allow the concept of conservation of energy to be used to predict and describe system behavior.Alignment agreement: The availability of energy limits what can occur in any system.Alignment agreement: | Models can be used to predict the behavior of a system, but these predictions have limited precision and reliability due to the assumptions and approximations inherent in models. Alignment agreement: Science assumes the universe is a vast single system in which basic laws are consistent.Alignment agreement: |
Common Core State Standards - Math
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Use appropriate measurements, equations and graphs to gather, analyze, and interpret data on the quantity of energy in a system or an object
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/cub_bernoulli_lesson01] to print or download.Pre-Req Knowledge
algebra and gas laws
Introduction/Motivation
(Note that Figures 1 and 2 are also available as PowerPoint slides in the Bernoulli Flow Graphics attachment. They are also suitable to print out as overhead transparencies or student handouts.)
Have you ever wondered how an airplane can fly? The simple answer is that as air flows around the wing, the plane is pushed up by higher pressure air under the wing, compared to lower pressure over the wing. But to understand this phenomenon more deeply, we must look at a branch of physics known as fluid mechanics, and in particular a principle known as the Bernoulli equation. Not only can this equation predict the air pressure around an airplane's wing, but it can also be used to find the force of high winds on a skyscraper, the pressure through a chemical reactor, or even the speed of water coming out of the hose in your backyard.
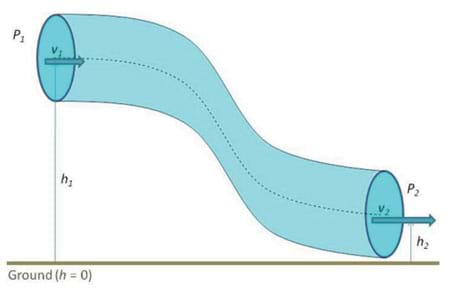
The Bernoulli equation states that for an ideal fluid (that is, zero viscosity, constant density and steady flow), the sum of its kinetic, potential and thermal energy must not change. This constraint gives rise to a predictable relationship between the velocity (speed) of the fluid, its pressure, and its elevation (relative height). Specifically, given two points along a streamline (an imaginary line tangent to the direction of flow, as shown in Figure 1), the Bernoulli equation states that:
where v is fluid velocity, ρ is fluid density, z is relative height, and P is pressure. Applying this equation to an example helps to make it clearer. Consider a reservoir located up in the mountains with a pipe leading down to a town at a lower elevation. The pipe delivers water to a hydroelectric plant, and we want to know how fast the water will flow into the plant turbines. Figure 2 illustrates this situation.

Now let's get back to how Bernoulli's principle applies to the wing of an airplane. When air flow is split around a wing, the air above the wing moves faster than the air below, due to the wing's shape. Since the velocity of the upper air increases, its pressure must decrease to maintain balance — as described in Bernoulli's equation. This results in greater pressure below the wing than above, which forces the wing upwards, enabling flight!
Lesson Background and Concepts for Teachers
The Bernoulli equation is an important expression relating pressure, height and velocity of a fluid at one point along its flow. The relationship between these fluid conditions along a streamline always equal the same constant along that streamline in an idealized system. An idealized system refers to a fluid that has a constant density (incompressible), and is inviscid.
Assuming that the fluid is inviscid means that it has no viscosity. Therefore, certain effects of viscosity, such as water sticking to the walls of its pipe or container, do not apply.
Because the Bernoulli equation is equal to a constant at all points along a streamline, we can equate two points on a streamline. Using information on the system at one point, we can solve for information at another.
According to the Venturi effect, a fluid's pressure decreases as its velocity increases. The Bernoulli equation puts this relationship into mathematical terms and includes a term for fluid height. To illustrate this relationship, consider water moving down a water slide. At the top where you load, the water is slow moving, pushed only by the water behind it. When the slide drops, the water rushes down quickly, increasing speed as it falls. Thus, the velocity is also affected by gravity through height. When all these terms are related and scaled for density and gravity, we have the Bernoulli equation, where v is fluid velocity, ρ is fluid density, h is relative height, and P is pressure. Notice the constant has units of pressure as well.
The Bernoulli equation can also be interpreted as an expression of conservation of energy, which can be formulated as
where KE is kinetic energy, PE is potential energy, and W is the work done on the system. Imagine a block of ice sliding down the water slide at some velocity. The block has a kinetic energy equal to one-half its mass times its velocity squared, or
where KE is kinetic energy and m is mass. The block also has a certain potential energy described by
where PE is the potential energy and h is the height. Finally, the work is being done on the block by the force of the water pressure behind it (with a force F=PA, where P is water pressure, and A is the area of the face of the ice that is getting pushed along). When the block is pushed a distance equivalent to its own width, Δx, then the work done on the block is
where V is volume. The equation for conservation of energy becomes
Dividing this equation by the volume, and recalling that density, ρΔ equals mass divided by volume, it reduces to
which is the Bernoulli equation.
Engineers can set the Bernoulli equation at one point equal to the Bernoulli equation at any other point on the streamline and solve for unknown properties. Students can illustrate this relationship by conducting the A Shot Under Pressure activity to solve for the pressure of a water gun! For example, a civil engineer might want to know how much pressure changes in a pipe between the top of a building and the ground.
Associated Activities
- A Shot Under Pressure - Students use their understanding of projectile physics and fluid dynamics to find the water pressure in a water gun. By measuring the range of the water jet, they are able to calculate the theoretical pressure. Students create graphs to analyze how the predicted pressure relates to the number of times they pump the powerful squirt gun.
Lesson Closure
Bernoulli's equation has a wide application of uses, from wing design to pipe flow. According to the Venturi effect, as fluid velocity increases, the pressure decreases and vice versa. Bernoulli's equation is a mathematical representation of this. Bernoulli's equation can be understood though manipulation of the energy of a flowing fluid. By setting Bernoulli's equation equal at two different points along a streamline, one can calculate the fluid conditions at one point by using information from another point.
Vocabulary/Definitions
Bernoulli Principle: In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. Named after Dutch-Swiss mathematician Daniel Bernoulli who published his principle in his book Hydrodynamica in 1738. Also called the Bernoulli effect.
inviscid flow: Flow in which one can ignore the effects of fluid viscosity.
streamline: A line tangent to the flow of a fluid at any given instant.
Venturi effect: The reduction in fluid pressure that results when a fluid flows through a constricted section of pipe. As a fluid's velocity increases, its pressure decreases, and vice versa. Named after Italian physicist Giovanni Battista Venturi (1746–1822).
Assessment
Pre-Lesson Assessment
Matching: To help students with this lesson and its associated activity, create a list of physics equations that they have already studied, such as kinetic energy, potential energy, work, kinematics equations. Randomly write the physics terms on the left side of the board and the matching halves of the equations (out of order) on the right side of the board. As a class, have students match the correct sides together. Examples:

Post-Introduction Assessment
Homework/Independent Practice: Have students complete the Bernoulli Equation Practice Worksheet. Have all students complete the first problem in class and review the answer together. Have students complete the second problem as homework.
Lesson Summary Assessment
Discussion Question: During the next class period, lead a five-minute discussion asking students what they learned from the homework assignment.
Additional Multimedia Support
You may want to use PowerPoint slides of Figure 1. Simple Pipe Flow, and Figure 2. Reservoir Example, with the class, as provided in the attached Bernoulli Flow Graphics.
See descriptions of additional real-life applications of Bernoulli's principle at the Science Clarified website: http://www.scienceclarified.com/everyday/Real-Life-Chemistry-Vol-3-Physics-Vol-1/Bernoulli-s-Principle-Real-life-applications.html
Show students an interactive animation of the Bernoulli Principle in the form of a cut-away view of a pipe with a shape that you can change using your computer's mouse, resulting changes in the pressure, cross sectional area and velocity of the fluid flowing through the pipe, which are graphed below the pipe. See Mark. Mitchell's website called, "Animated Demonstration of Bernoulli's Principle," at http://home.earthlink.net/~mmc1919/venturi.html
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to Pascal's law, Archimedes' principle and Bernoulli's principle. Fundamental definitions, equations, practice problems and engineering applications are supplied.

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

tudents are introduced to the similarities and differences in the behaviors of elastic solids and viscous fluids. In addition, fluid material properties such as viscosity are introduced, along with the methods that engineers use to determine those physical properties.

Students learn about the fundamental concepts important to fluid power, which includes both pneumatic (gas) and hydraulic (liquid) systems.
References
Bernoulli's principle (definition). Last updated February 11, 2010. Wikipedia, The Free Encyclopedia. Accessed February 17, 2010. http://en.wikipedia.org/w/index.php?title=Bernoulli%27s_principle&oldid=343435891
Knight, Randall. Physics for Scientists and Engineers: a Strategic Approach. Second edition. San Francisco, CA: Pearson Addison-Wesley, 2008.
Munson, B. R., Young, D.F., Okiishi, T.H. Fundamentals of Fluid Mechanics. Fifth edition. New York, NY: John Wiley & Sons, Inc., 2006.
Venturi effect (definition). Last updated February 12, 2010. Wikipedia, The Free Encyclopedia. Accessed February 17, 2010. http://en.wikipedia.org/w/index.php?title=Venturi_effect&oldid=343508711
Other Related Information
Browse the NGSS Engineering-aligned Physics Curriculum hub for additional Physics and Physical Science curriculum featuring Engineering.
Copyright
© 2009 by Regents of the University of ColoradoContributors
James Prager; Karen King; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program and Laboratory, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: January 28, 2021








User Comments & Tips