Quick Look
Grade Level: 11 (10-12)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Algebra, Biology, Physics, Reasoning and Proof
NGSS Performance Expectations:

| HS-PS2-6 |
Summary
Students are introduced to the similarities and differences in the behaviors of elastic solids and viscous fluids. Several types of fluid behaviors are described—Bingham plastic, Newtonian, shear thinning and shear thickening—along with their respective shear stress vs. rate of shearing strain diagrams. In addition, fluid material properties such as viscosity are introduced, along with the methods that engineers use to determine those physical properties.
Engineering Connection
Engineers often design devices that transport fluids, use fluids for lubrication, or operate in environments that contain fluids, such as engines, printers and pacemakers. Thus, it is important for engineers to understand how fluids behave under various conditions. Understanding fluid behavior can help engineers to select the best fluid to operate in a device or to design devices that are able to efficiently and harmlessly operate in environments that contain fluids.
Learning Objectives
After this lesson, students should be able to:
- Describe the similarities and differences between elastic solids and viscous fluids.
- Explain four different types of fluid behavior: Newtonian, shear thinning, shear thickening, and Bingham plastic.
- Demonstrate an understanding of how engineers measure and calculate fluid material properties such as viscosity.
- Communicate scientific information about why the molecular-level structure is important in the functioning of designed materials.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-6. Communicate scientific and technical information about why the molecular-level structure is important in the functioning of designed materials. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Communicate scientific and technical information (e.g. about the process of development and the design and performance of a proposed process or system) in multiple formats (including orally, graphically, textually, and mathematically). Alignment agreement: | Attraction and repulsion between electric charges at the atomic scale explain the structure, properties, and transformations of matter, as well as the contact forces between material objects. Alignment agreement: | Investigating or designing new systems or structures requires a detailed examination of the properties of different materials, the structures of different components, and connections of components to reveal its function and/or solve a problem. Alignment agreement: |
Common Core State Standards - Math
-
Describe qualitatively the functional relationship between two quantities by analyzing a graph (e.g., where the function is increasing or decreasing, linear or nonlinear). Sketch a graph that exhibits the qualitative features of a function that has been described verbally.
(Grade
8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Science
-
Gather, analyze and interpret data on chemical and physical properties of elements such as density, melting point, boiling point, and conductivity
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Texas - Science
-
analyze physical and chemical properties of elements and compounds such as color, density, viscosity, buoyancy, boiling point, freezing point, conductivity, and reactivity;
(Grades
9 -
10)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/cub_surg_lesson03] to print or download.Pre-Req Knowledge
Students should understand the content presented in the Mechanics of Elastic Solids lesson. They should also have an understanding of algebra, how to solve algebraic equations, and how to read and interpret graphs.
Introduction/Motivation
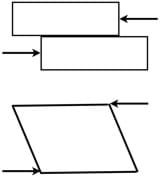
We previously talked about elastic solids; today we will learn about viscous fluids.
Let's review what we know about solids and fluids. What is a solid? What is a fluid? (Listen to student descriptions.) A solid is a material that has structural rigidity and resistance to change in shape or volume. In other words, solids maintain their shapes and do not form to their containers. A fluid, either liquid or gas, can flow to take the shape of its container. More formally, a fluid is a substance that continuously deforms or flows under an applied shear stress.
Shear stress is a little different than the stress we discussed in the solid mechanics lesson. To understand shear stress, first think of two blocks sliding against each other (draw Figure 1-top on the classroom board). A force pushes towards the left on the top block and a force pushes to the right on the bottom block. The opposing forces on the different blocks cause the sliding motion.
Now imagine that instead of having two rigid blocks we have one block of Jell-O. When we apply similar forces on the Jell-O block, the deformation is similar to the two rigid blocks (draw Figure 1-bottom). Imagine that the Jell-O is sliding internally. Since the Jell-O is a solid, it will only undergo a certain amount of deformation before either breaking or resisting the forces, which prohibits any further deformation. What the Jell-O experiences is defined as shear stress. Shear stress is experienced in materials when you have these "sliding" forces. Now imagine shear stress on a fluid. With a fluid, it will continuously deform—which is the definition of a fluid. In this lesson, we will learn how engineers study fluids and what similarities and differences this analysis has with solids.
Fluid mechanics is the study of how fluids react to forces. Fluid mechanics includes hydrodynamics, the study of force on liquids, and aerodynamics, the study of bodies moving through air. Fluid mechanics encompasses a wide variety of applications. Can you think of some examples? (Listen to student ideas.) Environmental engineers use fluid mechanics to study pollution dispersion, forest fires, volcano behavior, weather patterns to aid in long-term weather forecasting, and oceanography. Mechanical engineers implement fluid mechanics when designing sports equipment such as golf balls, footballs, baseballs, road bikes and swimming gear. Bioengineers study medical conditions such as blood flow through aneurysms. Aerospace engineers study gas turbines that launch space shuttles and civil engineers use fluid mechanics for dam design. With just these few examples of the wide variety of applications of fluid mechanics, you can see how fluid mechanics is an important area of study for many types of engineering.
(Continue on to present students with the content in the Lesson Background section.)
Lesson Background and Concepts for Teachers
(optional: Be ready to show students the attached seven-slide Viscous Fluids Presentation PowerPoint, along with the information below. Also bring to class a bottle of honey and a bottle of water to show students.)
Pass around the class a bottle of honey and a bottle of water (or ask students to imagine these two fluids). Have students compare the properties of each and give some examples of why fluids with these properties might be useful in some systems and why they would not work in other systems. Examples: A thick fluid, such as toothpaste, stays on a toothbrush, whereas a fluid that moves easily like water just runs off. A fluid like water might be useful in a thermometer because it is easy to move and does not leave any residue on its container. If a fluid like honey was used in a thermometer, it would stick to the sides and cause difficulty in reading the measurement gauge. Can you think of other example applications?
From examining and comparing these two fluids, we can conclude that the honey is good at coating things and the water is good if you need a fluid to move with little force. What we just observed is a difference in viscosity. Fluids with different viscosities can be useful for different applications.
Viscosity is how engineers measure the resistance of fluids to shear stress. Less-viscous fluids deform easier with applied shear, thus water is less viscous than honey. Engineers calculate the viscosity of a fluid with the following equation:
where τ (tao) is the shear stress in the fluid, μ (nu) is the viscosity, and du/dy is the shear velocity of the fluid. The shear stress of a fluid is defined in a similar manner as stress in a solid: force divided by area. The above equation is very similar to the Hooke's law equation (discussed in the Mechanics of Elastic Solids lesson):
where σ (sigma) is the stress in the solid, E is Young's modulus, and ε is the strain that the solid experiences. In each equation, the stress in the material (caused by a force on the material) is equal to a material property (Young's modulus or viscosity) multiplied by either the strain or velocity of the material, which tells something about the response of the material to the force (either moving the material or deforming it). Therefore, the Young's modulus and viscosity are similar in that they both measure a material's resistance to deformation (or movement).
The viscosity equation is useful for calculating a material's viscosity when you know the force being applied to the fluid and the resulting velocity. Knowing the viscosity helps engineers know how a fluid will behave under different circumstances. Engineers also use this equation when designing devices. By using a fluid with a known viscosity and applying a force to it, engineers can calculate how fast the fluid will move. Here are examples of how this equation can be used to help engineers with real situations:
- For example, at your neighborhood gas station, the pumps are designed to measure the volume of gasoline being purchased. By knowing the viscosity of the fluid and the force being applied to it from the gas pump, engineers can calculate the velocity that the gas will move. Using this information, along with the dimensions of the gas nozzle, the amount of gas being purchased can be calculated.
- For example, if engineers know the viscosity of printer ink and what velocity they want the ink to move, they can design a printer so that the correct amount of force is applied to the ink.
- For example, for the mass production and packaging required in the food and beverage industry, knowing the viscosity of the fluids to be packaged (think milk vs. molasses) gives engineers the information they need to design factory equipment that regulates how fast a fluid can be packaged based on the tolerable forces that can be applied to the fluid.
Measuring Viscosity
How do engineers determine the viscosity of fluids? We know that mechanical testing systems calculate Young's modulus by deforming a material and recording the force applied and the displacement that the material undergoes. Young's modulus is similar to viscosity, so engineers use similar methods to calculate the properties of fluids. Engineers primarily use one of two methods, depending on whether the fluid is Newtonian or not.
- For Newtonian fluids, engineers place the fluid in a container and drop a ball of known mass and volume into the container. By measuring the amount of time it takes the ball to travel through a specified distance of the fluid, they can calculate the resistance the ball experiences through the fluid. (This is similar to the forces a skydiver experiences when jumping out of an airplane. At some point, the force of air resistance matches the force of gravity and the skydiver reaches terminal velocity—the point at which the skydiver no longer accelerates and reaches a constant velocity.) For the ball with a known mass and shape, calculating the force of gravity on the ball is easy. This force must balance with the force of shear resistance (viscosity) and dictates the ball's speed (velocity). So if an engineer can measure the speed of the ball, s/he can directly predict the viscosity of the fluid! (Students investigate this method in more detail during the associated Measuring Viscosity activity.)
- The second method for determining viscosity, rheometry, is very expensive and typically used only on fluids that are not Newtonian. A rheometer (see Figure 2) can either control the velocity of a fluid and measure the force it takes to apply that velocity, or apply a force and measure the resulting velocity. Using either method, engineers acquire the force and velocity data needed to use the viscosity equation and calculate the viscosity of the fluid. In the testing machine, the fluid is placed either in a cylinder or on a plate, and different probes are used to apply force to the fluid (Figure 2-right). The probe can vary in geometry, depending on the fluid viscosity. High-viscosity fluids are placed on plates with either a cone or another flat plate used to apply the force (Figures 2b, 2c). All other fluids, especially low-viscosity fluids, require a cylinder configuration (Figure 2a).
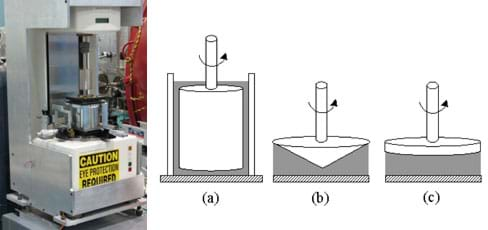
Figure 2. Rheometers are used to measure the viscosity of non-Newtonian fluids. Different rheometer sample holders and probes are used, depending n the viscosity of test fluid. Low-viscosity fluids require a dual cylinder configuration (a). High-viscosity fluids, such as pastes and gels, are placed on a plate with either a cone (b) or a parallel flat plate (c) that applies shear to the fluid.
Fluid Behavior
Using a rheometer or a drop ball test, engineers collect the data needed to create shear stress (τ) vs. rate of shearing strain diagrams (du/dy). The shear stress is calculated using the force data, and the rate of shearing strain is calculated using the deformation data. This is similar to a stress-strain diagram with solids. When engineers test solids and generate stress-strain diagrams, they calculate the slope of the initial line (covered in more detail in the Mechanics of Elastic Solids lesson), which is equal to the Young's modulus or stiffness of the material. With fluids, engineers also calculate the slope of the line formed on the shear stress-rate of shearing strain diagram. This value is equal to the viscosity of the fluid.
Looking at the resulting diagrams, engineers can identify four fluid behaviors: Bingham plastic, Newtonian, shear thinning, and shear thickening (see Figure 3).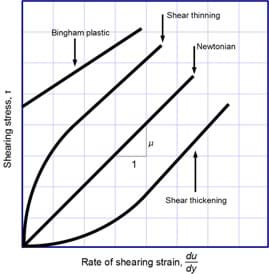
Bingham plastic materials behave as solids at low stresses, but flow as viscous fluids at high stresses. Because the particles in these materials have weak bonds, at high stresses they break, causing them to flow and be characterized as fluids. When the stress is relieved, the bonds form again, characterizing the materials as solids. Two material properties are needed to describe this material: viscosity and yield stress. The slope of the shear stress-rate of shearing strain diagram is the viscosity (as described above) and the intersection of the y-axis (shear stress axis) is the yield stress. The yield stress defines the transition point between solid and liquid.
- A common example of this fluid type is toothpaste.
Newtonian fluids are identified by linear plots in the diagram, which means that these fluids have constant viscosities that are independent of velocity (rate of shear). Regardless of how fast or slow you stir these liquids, they always require the same proportional forces.
- Everyday examples of this fluid type include: water, gasoline and most gases (remember gases are fluids as well!).

A range of fluid behavior examples: toothpaste (Bingham plastic); water (Newtonian); whipped cream (shear thinning) and body armor (shear thickening).
For shear thinning materials, viscosity decreases as velocity (rate of shear) increases. As you stir this type of fluid faster, it becomes much easier to stir. While scientists do not fully understand the cause of this phenomenon, engineers have used fluids with this behavior to their advantage.
- For example, paint is a shear thinning fluid. It is easy to adhere on a roller because of the increase in velocity the roller imposes on the fluid. However, once the paint is applied to the wall and the force on the fluid is reduced, the viscosity increases to its original state and the paint stays on the wall without dripping.
- Another example is whipped cream. Engineers used its characteristics to their advantage when designing pressurized can containers for easy dispensing of whipped cream. When a force is applied to this fluid, its viscosity decreases and it flows smoothly like a liquid out of the nozzle. Once it comes to a rest on your tasty treat, it becomes rigid again (increased viscosity), like a solid.
- Additional common examples include ketchup, blood and motor oil.
For shear thickening materials, viscosity increases as velocity (rate of shear) increases. As you stir this type of fluid faster, it becomes much harder to stir. This is due to closely packed particles combined with just enough fluid to fill the spaces between them. At low velocities, the fluid dominates the behavior and is able to continue to adequately fill the spaces between the particles because they are not moving fast. At high velocities, the fluid cannot keep up with the particle movement and is unable to fill the spaces between them, so the particles to rub against each other creating friction between them. Engineers have also used this phenomenon to improve our lives.
- One example is body armor. The fluid in body armor reacts to sudden forces (increases in velocity, such as bullets) and immediately increases its viscosity, which in turn stops the blow (the bullets). The only caveat to this is that slow velocities (like a knife) do not produce this change in viscosity. To address this vulnerability, an additional material (Kevlar fabric) is added to body armor to protect against these types of attacks. The combination of Kevlar and a shear thickening fluid performs better at protecting than Kevlar alone. The fluid-Kevlar combination body armor is also one-third the thickness of body armor containing only Kevlar, so it is more lightweight and comfortable to wear.
- Another innovative design using shear thickening fluids is found in vehicle traction control, which is a system used for all-wheel drive vehicles that reacts to the differences in motion between the front and rear wheels. When the vehicle has sufficient traction, the front and rear wheels have similar motion, so no shear force is applied to the fluid. However, when the primary drive wheels begin to slip, the difference in motion between the front and rear increases, applying a shear force to the fluid and resulting in an increase in viscosity. This viscosity increase applies torque to the secondary drive wheels, creating a system in which all four wheels become engaged only when needed.
- Another example is cornstarch in water; see the Additional Multimedia Support section for the link to a fun online video that demonstrates its behavior in response to different forces.
Associated Activities
- Measuring Viscosity - Students calculate the viscosity of various household fluids by measuring the amount of time it takes marble or steel balls to fall given distances through the liquids. They experience what viscosity means, and also practice using algebra and unit conversions.
Lesson Closure
In conclusion, fluids exhibit very similar behavior to elastic solids and can therefore be analyzed with similar equations. One way of characterizing fluids is by their viscosities, which is a measure of a fluid's resistance to shear stress.
How do engineers measure viscosity? They measure viscosity either by dropping a ball in the fluid and measuring the amount of time it takes the ball to travel through the fluid, or by using a rheometer. If a fluid has a constant viscosity with varying velocities, then it is defined as a Newtonian fluid. If the fluid has different viscosities with varying velocities then it could be defined as shear thinning, shear thickening, or Bingham plastic.
Understanding fluid behavior is important to engineers; it helps them select the optimum fluids to operate in devices that they are designing and create devices that are able to efficiently operate in environments that contain fluids.
Vocabulary/Definitions
Newtonian fluid: A fluid with a viscosity that is independent of its velocity (rate of shear).
strain: Deformation per unit length.
stress: Force per unit area, or intensity of forces distributed over a given section.
torque: A force that causes an object to rotate.
velocity: Speed (and direction) of an object.
viscosity: A measure of the resistance of a fluid to shear stress.
Young's modulus: A measure of the stiffness of a material.
Assessment
Worksheet: After presentation of the lesson content, have students complete the attached Viscosity Worksheet. Review their answers to gauge their mastery of the subject matter.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to the concept of viscoelasticity and some of the material behaviors of viscoelastic materials, including strain rate dependence, stress relaxation, creep, hysteresis and preconditioning. Viscoelastic material behavior is compared to elastic solids and viscous fluids.

Students calculate stress, strain and modulus of elasticity, and learn about the typical engineering stress-strain diagram (graph) of an elastic material.

Students explore the basic characteristics of polymers through the introduction of two polymer categories: thermoplastics and thermosets. During teacher demos, students observe the unique behaviors of thermoplastics.

Students calculate the viscosity of various household fluids by measuring the amount of time it takes marble or steel balls to fall given distances through the liquids. They experience what viscosity means, and also practice using algebra and unit conversions.
Copyright
© 2011 by Regents of the University of Colorado.Contributors
Brandi N. Briggs; Michael A. Soltys; Marissa H. ForbesSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
This digital library content was developed by the Integrated Teaching and Learning Program under National Science Foundation GK-12 grant no. DGE 0338326. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: May 1, 2025









User Comments & Tips