Lesson Mechanics of Elastic Solids

Learning Objectives

After this lesson, students should be able to:

• Describe the importance of understanding solid mechanics during device design.
• Calculate stress, strain and modulus of elasticity.
• Explain how engineers measure and calculate elastic material properties such as elastic modulus.
• Explain a typical engineering stress-strain diagram of an elastic material and its important features.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Worksheets and Attachments

Pre-Req Knowledge

Students should have completed the Using Hooke's Law to Understand Materials activity. Students should have an understanding of algebra, how to solve algebraic equations, and how to read and interpret graphs.

Introduction/Motivation

(Begin by conducting the associated activity Using Hooke's Law to Understand Materials; then proceed to conduct the lesson. Students benefit significantly by completing the activity first because the lesson material is so new and different than anything they have done before and so it helps to have the hands-on reference of what they learned in the activity while learning the theory. We found that when the lesson was taught first, students were completely lost and did not grasp the concepts nearly as well as when the activity was completed first.)

Why are we studying tissue mechanics when we are trying to design a device? Why study mechanics at all? An understanding of mechanics is useful for the analysis and design of load-bearing structures such as, buildings, skyscrapers, bridges, space shuttles, prosthetics and biological implants.

As an example, the World Trade Center's design optimized several different types of steel. The engineers performed a stress analysis of the building components to understand the type of forces to which each beam would be exposed. From this, engineers were able to choose the right type of steel for each part of the structure. If high performance steel was not needed in certain parts of the building, they did not use it, since it is very costly. This approach makes sense, but also leads to an explanation of why these buildings collapsed. When the plane hit the building, an extremely unlikely event, it knocked out several of the beams that held up the building. When these beams were removed, the rest of the beams were forced to support the entire weight of the structure, but they were not strong enough. The remaining beams could not handle the increased stress (weight) from the floors above and they buckled (failed).

An example of a biological implant is a hip replacement. To prevent failure of the replacement implant, engineers analyze the stresses normally present in human hip bones to ensure that an artificial hip bone is able to withstand the stress that the natural joint withstood. On the other hand, we do not want the implant to take on too much of the stress from the surrounding bone or the bone will begin to disintegrate because the human body sees unused bone as not needed. If this happens, the implant becomes loose in the bone and must be repaired with another surgery. So, you can see that it is important to study the materials that you use in your design, but it is also important to study the material properties of the surrounding environment that your device will interact with and function in.

In addition, engineers also study mechanics in order to characterize materials. During material selection, engineers must know how a given material is expected to behave in certain situations, so engineers test and characterize the materials and publish the material properties.

For the design project in this course, we need to understand how the materials in our bodies behave in response to forces so that we can design devices that will not harm the body. Biological materials have a complex response to forces. To understand this response, we need to first understand mechanics of elastic solids, which is the most basic level of material behavior. Then, we will explore the world of fluids and learn how fluids react to forces. Finally, we will combine what we know about the mechanics of solids and fluids to understand viscoelastic materials, such as those found in the human body.

(Continue presenting students with the information provided in the Lesson Background section. Then have students complete the attached worksheet and homework.)

Lesson Background and Concepts for Teachers

Introduction to Solid Mechanics

(In advance, make copies of the Solid Mechanics Worksheet and Solid Mechanics Homework, one each per student. Also, prepare to show students the attached 14-slide Mechanics of Elastic Materials Presentation PowerPoint to accompany presentation of the following material. The slides are "animated" so you can click to show the next item when ready.)

Elastic solids are characterized as materials that behave like springs. As long as they are not permanently deformed, it always takes the same amount of force to displace the material the same amount and when the force is released the material returns to its original dimensions. This can be compared to a spring. If you hang a weight on a spring and measure the amount it stretches and then release the weight, then the spring returns to its original length. If you hang the same weight from the spring again, then the spring stretches the same amount as it did the first time. This is the response of elastic solids (as long as the force is not big enough to permanently deform the material). We observed this response in the Using Hooke's Law to Understand Materials activity, so now we are going to explore the mathematics and theory of this response in detail and learn how engineers analyze elastic material behavior.

Similar to what we observed in the Using Hooke's Law to Understand Materials activity, engineers test materials by recording the force applied to the material and its corresponding displacement. This gives engineers information on how a material reacts to a force. From the force data, engineers calculate the stress present in the material and from the displacement data they calculate the strain that the material experienced. Once these values are known, they calculate a property of the material called the modulus of elasticity, and start comparing materials to one another. By knowing the modulus of elasticity, engineers know how that material responds to certain forces. Let's take a closer look into stress, strain and modulus of elasticity.

Stress is the force per unit area, or intensity of the forces distributed over a given section. It is defined mathematically through the following equation:

σ (sigma) is the Greek letter that represents stress, F is the force being applied to the material, and A is the cross sectional area of the material. The standard unit for force is Newtons (N) and the standard unit for area is meters squared (m²). This gives the standard unit for stress of Pascals (Pa), a measure of pressure.

Stress is how engineers normalize the force that is applied to a material to account for differences in geometry. To illustrate the importance of normalizing, let's compare two rods of the same material that are the same length but different cross sectional areas. The force required to stretch the two rods the same amount (or break them) is different; the large cross sectional area rod takes a lot more force to deform (or break). However, if we normalize the force to account for the difference in cross sectional area, then we see that the stress in the material at failure is the same. So the stress it takes to deform (or break) that material is the same no matter what its geometry. This is useful for predicting failure conditions for materials. If you know the yield stress of a material and you know its dimensions, then you can calculate how much force that material can withstand before failing.

Strain is deformation per unit length. Strain is defined mathematically through the following equation:

ε (epsilon) is the Greek letter that represents strain, ΔL (delta L) is the change in length of the material due to the force being applied, and L_o is the initial length of the material without any forces acting on it. The standard unit for change in length and initial length is meters (m). Thus, no unit exists for strain; it is unitless.

Strain is how engineers normalize the deformation that a material experiences to account for differences in geometry. Normalizing deformation is also important. If we compare a very long rod to a very short rod and they have the same cross sectional areas and are the same material, then the same amount of displacement will be more detrimental to the short piece. The displacement may be on the same order of magnitude as the short piece but on a smaller order of magnitude than the long piece. This may mean that the short piece breaks but the long piece does not, even though they were stretched the same amount. Strain normalizes the displacement so that the geometry does not matter. Both materials will break at the same strain even though it will not be the same displacement. This is useful for determining how much a material can be deformed before failure. The yield stress discussed above corresponds to a certain strain. This is useful because it is easier to measure a material's deformation to calculate strain than it is to determine the forces on a material. Thus, engineers analyze the strain present in the material and then map the strain to the corresponding stress for that type of material to predict whether or not it will fail. So, if you can calculate the strain, then you can still predict the failure conditions of your selected material.

Modulus of Elasticity is a representation of the stiffness of a material that behaves elastically. Modulus of elasticity is explained mathematically through the following equation:

E represents the modulus of elasticity, σ is the stress in the material, and ε is the strain that the material experiences due to the stress. The standard unit for stress is Pascals and strain is unitless, so the unit for modulus of elasticity is also Pascals (Pa).

Modulus of elasticity is how engineers characterize elastic material behavior. This is useful for knowing how materials behave, material selection for device design, and calculating stress in a material since it is easier to measure deformation than it is to determine the exact force on a material. The modulus of elasticity is similar to the stiffness, k, of springs.

In-Class Examples

(With the students, review the three examples included in the attached presentation file, and then have students individually complete the worksheet. Then continue presenting the material, below, followed by the homework handout.)

Measuring Modulus of Elasticity

Modulus of elasticity and yield stress are two common material properties that can be calculated from performing tensile tests with a mechanical testing system. Mechanical testing systems are designed so that engineers can clamp the selected material between two grips. The bottom grip remains stationary while the top grip moves up at a specified displacement rate. The testing system records the amount of force that it takes to stretch the material and the corresponding displacement of the grips. As described earlier, engineers measure the initial cross sectional area of a specimen and the initial length between the grips so that they can calculate stress from the force data and strain from the displacement data. This data is used to create what engineers call stress-strain diagrams.

So that engineers can select materials for their devices that meet the design requirements, many materials have been tested numerous times and their properties published in materials handbooks. For material properties to be published so that all engineers can use them without testing the materials themselves, a set of standards was put into practice to ensure that testing is conducted in the same manner for all materials. One important part of these standards is the geometry of the test specimen. If the test specimen is a rectangle, then often a higher stress state is experienced at the grips. This is due to the grips and cannot be avoided with this type of test. It results in the specimen breaking at the grips such that engineers cannot accurately calculate the stress that caused the material to break. To solve this problem, engineers developed a different geometry that eliminates this source of error: the dog bone shape (see Figure 1). The dog bone shape is larger at the top and bottom where the grips attach to the specimen and the cross sectional area is smaller between the grips. The smaller cross sectional area allows the stress to be concentrated in the center of the specimen so that the effects of the grips do not interfere with testing. Using this specimen shape, engineers can be sure that the stress measured by the testing system is the stress state actually experienced by the material.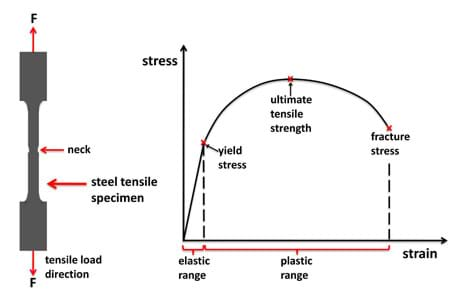

Figure 1 shows an example dog bone-shaped specimen and a typical stress-strain diagram for a ductile, elastic material such as steel. Engineers gather much useful information from this diagram to learn about the behavior of a material, including its modulus of elasticity and yield stress. Let's look more closely at this graph and explain the most important features that engineers use and record.

The elastic range is defined by the linear portion of the stress-strain curve. The slope of this line is defined by the modulus of elasticity. Remember that E= stress/strain, which is the same equation that defines the slope of this line (m=y/x). If a material is stretched only in this region and then the force is released, then the material follows the same line down while being unloaded. The material thus returns to its original dimensions. Again, this is seen with a spring; when it is stretched and then released, it returns to its original configuration.

The plastic range is the portion of the diagram to the right of the elastic region; this is the region of permanent deformation. If a material is stretched into this region, then it starts to permanently deform. When the force is released, the unloading curve is linear with the same slope as the elastic range, so it does not following its loading curve. The line never reaches the origin again and thus the material never returns to its original configuration. The amount of permanent deformation is defined by the intersection along the x-axis of the unloading curve. If you have ever stretched a spring too much (perhaps while playing with a slinky), you have experienced this plastic region and have observed permanent deformation. No matter how hard you try, the spring will not go back to its original configuration.

Yield stress is the minimum stress that causes permanent deformation. Since permanent deformation may define failure of a component in a device, engineers want to design devices so that no component is exposed to forces that produce the yield stress in its material. If this happens, it leads to failure; this is why engineers often use the yield stress value when designing systems.

Ultimate tensile stress is the maximum stress that a material can withstand; it is the maximum point on the diagram. At this point, necking begins, and the material starts down a slippery slope to ultimate failure.

Necking is a localized decrease in cross sectional area. If the specimen is dog bone-shaped, necking typically occurs at the middle of the specimen. Before this point, the entire specimen decreases in cross sectional area because it is being stretched and the area decreases uniformly over the entire specimen. After the ultimate tensile stress is reached, only one area of the specimen continues to decrease in cross sectional area. This causes a decrease in stress as the strain increases, meaning that as you continue to stretch the material it takes less force to pull on it. This is very counterintuitive. Note: Stress is calculated using the cross sectional area, but since the cross sectional area is continuing to change during the test and it is difficult to measure how the area changes, engineers often calculate the stress using the initial cross sectional area throughout the entire test. This is called engineering stress.

Fracture stress is stress in which the material fails. This is the last stress state that a specimen experiences before it fractures.

Associated Activities

• Using Hooke's Law to Understand Materials - Students explore the response of springs to forces as a way to begin to understand elastic solid behavior. They gain experience in data collection, spring constant calculation, and comparison and interpretation of graphs and material properties to elucidate material behavior. (Conduct this activity before the lesson.)

Vocabulary/Definitions

ductile: A material that can permanently deform before failure.

mechanics: The study of how materials and systems react to forces and displacements.

modulus of elasticity: A measure of the stiffness of a material.

normalize: To standardize.

strain: Deformation per unit length.

stress: Force per unit area, or intensity of forces distributed over a given section.

tensile test: A test in which the material is subjected to pulling forces until failure.

yield stress: The minimum stress that causes permanent deformation.

Assessment

Worksheet: After going over the three in-class examples with students, have them complete the attached Solid Mechanics Worksheet. Review their answers to gauge their mastery of the subject matter.

Homework: At lesson end, have students complete the attached Solid Mechanics Homework. Review their answers to gauge their mastery of the subject matter.

Copyright

Contributors

Supporting Program

Acknowledgements

This digital library content was developed by the Integrated Teaching and Learning Program under National Science Foundation GK-12 grant no. DGE 0338326. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.