Quick Look
Grade Level: 11 (10-12)
Time Required: 1 hours 15 minutes
Lesson Dependency:
Subject Areas: Physical Science, Physics
Summary
Students are introduced to Hooke's law as well as stress-strain relationships. First they learn the governing equations, then they work through several example problems, first individually, then as a class. Through the lesson's two-part associated activity, students 1) explore Hooke's law by experimentally determining an unknown spring constant, and then 2) apply what they've learned to create a strain graph depicting a tumor using Microsoft Excel®. After the activities, the lesson concludes with a stress-strain quiz to assess each student's comprehension of the concepts.Engineering Connection
More than 300 years ago, Robert Hooke identified a proportionality that has remained a fundamental concept to physicists and engineers to this day. Though his "law" was established for the case of springs alone, it has since been related to all materials of known surface area. The relationship used most readily today is the direct proportionality between stress and strain. Together, civil engineers, mechanical engineers and material scientists, carefully select structural materials that are able to safely endure everyday stress while remaining in the elastic region of the stress-strain curve, otherwise permanent deformation occurs. Architects who once chose stone for its aesthetic appeal now choose steel for its long-term endurance. For biomedical engineers, titanium is often the material of choice for its biocompatibility and more importantly, its capability to withstand the tensile and compressive stress of the body's weight. In the provided problem set, students explore applications of Hooke's law and stress-strain relationships. In problem 7 especifically, students apply these relationships to the case of body tissue, as biomedical engineers would.
Learning Objectives
After this lesson, students should be able to:
- Explain the stress and strain concepts and the relationship between them.
- Explain Hooke's law and apply it to analyze springs.
- Use Microsoft Excel® to make a simple strain plot.
- Relate stress and strain to the unit's engineering challenge.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Prove that, given a system of two equations in two variables, replacing one equation by the sum of that equation and a multiple of the other produces a system with the same solutions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Telemedicine reflects the convergence of technological advances in a number of fields, including medicine, telecommunications, virtual presence, computer engineering, informatics, artificial intelligence, robotics, materials science, and perceptual psychology.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use computers and calculators to access, retrieve, organize, process, maintain, interpret, and evaluate data and information in order to communicate.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Optimize a design by addressing desired qualities within criteria and constraints.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use various approaches to communicate processes and procedures for using, maintaining, and assessing technological products and systems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Maryland - Science
-
Motion and Stability: Forces and Interactions
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Tennessee - Math
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Prove that, given a system of two equations in two variables, replacing one equation by the sum of that equation and a multiple of the other produces a system with the same solutions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Tennessee - Science
-
Solve problems related to velocity, acceleration, force, work, and power.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_cancer_lesson2] to print or download.Pre-Req Knowledge
A basic understanding of algebra and the ability to solve simple algebraic expressions. In addition, an understanding of the cancer detection challenge, as introduced in the previous lesson.
Introduction/Motivation
In today's lesson, we will begin to learn about Hooke's law and then we learn how to apply this proportionality to body tissue. We will learn exactly what the terms stress and strain describe as well as the relationship between them. After going through the lesson's material, I will pass out a handout with example problems. Work these to the best of your abilities independently first; then we will review the problems as a class.
After becoming familiar with using the new equations, we will explore Hooke's law in an associated activity (Applying Hooke's Law to Cancer Detection) by experimentally determining an unknown proportionality constant. After exploring Hooke's law, in the second portion of the activity, we will begin to apply what we've learned to develop a means of imaging body tissues and we will soon be able to detect malignant tumors!
You will also practice graphing prepared data to depict cancerous tissue. After we have mastered this material, we will have a quiz on stress, strain and Hooke's law. Please take careful notes and be sure to ask any questions you have about the example problems we will be working through.
Referring back to the legacy cycle which we discussed in the previous lesson, today's lesson constitutes the research and revise phase. Refer back to your initial thoughts notes and record any new information that applies to solving the challenge. Your goal today is to review, revise and expand your current knowledge! Now, let's learn how to detect cancer.
Lesson Background and Concepts for Teachers
Legacy Cycle Information
This lesson falls into the Research and Revise phase of the legacy cycle. Students begin to learn the basic concepts required for creating a strain graph to depict cancerous tissue. Following this lesson, have students revise their initial thoughts and at the conclusion of the associated activity, students should have the skills necessary to Go Public with a solution. But before Going Public, have students complete the Stress, Strain and Hooke's Law Quiz as part of the Test Your Mettle phase of the legacy cycle. The quiz serves as a formative assessment while the next lesson's Go Public phase provides a summative assessment.
Lecture Information
In the late 1600s, Robert Hooke stated that "The power of any springy body is in the same proportion with the extension." Though Hooke's law has remained valid today, the wording has been corrected, replacing power with force. The law is explained by a direct proportionality between a spring's compression or expansion and the restoring force which ensues. The relationship is given by F= -k * Δx where Δx is the distance a spring has been stretch, F is the restoring force exerted by the spring and k is the spring constant which characterizes elastic properties of the spring's material. This law is valid within the elastic limit of a linear spring, when acting along a frictionless surface.
Extending Hooke's exploration of springs, it becomes apparent that most materials act like springs with force being directly proportional to displacement. But as compared to springs, other materials possess an area which must be accounted for. Replacing force with a measure of stress and displacement with a measure of strain, the following expression may be obtained, σ = E* ε. We will now explore the measures of stress and strain.
Stress is a measure of average force per unit area, given by σ = F/A where average stress, σ, equals force, F, acting over area, A. The SI unit for stress is pascals (Pa) which is equal to 1 Newton per square meter. The Psi is an alternative unit which expresses pounds per square inch. The units of stress are equal to the units of pressure which is also a measure of force per unit area.
Stress cannot be measured directly and is therefore inferred from a measure of strain and a constant known as Young's modulus of elasticity. The relationship is given by σ = E* ε, where σ represents stress, ε represents strain and E represents Young's modulus of elasticity. Using this means of inferring stress, strain is a geometrical measure of deformation and Young's modulus is a measure used to characterize the stiffness of an elastic material. Strain does not carry a unit but the units of Young's modulus are Pa.
Strain is characterized by the ratio of total deformation or change in length to the initial length. This relationship is given by ε = Δl/l 0 where strain, ε, is change in l divided by initial length , l 0 .
The following problems may be worked independently and reviewed as a class, encouraging students to become more familiar with using the equations given above. Give each student a copy of the Stress, Strain and Hooke's Law Problem Set.
You are required to SHOW ALL WORK. Useful constants that are provided in a table below. (assume given constants have three significant figures (SF). Please also note that the relationships we have just discussed are given below.
Material
- steel
- Young's module: 200x109 E(Pa)
- cast iron
- Young's module: 100x109 E(Pa)
- concrete
- Young's module: 20.0x109 E(Pa)
F=m*a σ=F/A ε = Δl/l0 σ = E* ε F= -k * Δx
- A 3340 N ball is supported vertically by a 1.90 cm diameter steel cable. Assuming the cable has a length of 10.3 m, determine the stress and the strain in the cable.
- Consider an iron rod with a cross-sectional area of 3.81 cm2 that has a force of 66,700 N applied to it. Find the stress in the rod.
- A concrete post with a 50.8 cm diameter is supporting a compressive load of 8910 Newtons. Determine the stress the post is bearing.
- The concrete post in the previous problem has an initial height of 0.55 m. How much shorter is the post once the load is applied (in mm)?
- A construction crane with a 1.90 cm diameter cable has a maximum functioning stress of 138 MPa. Find the maximum load that the crane can endure.
- Consider Hooke's law as a simple proportionality where F is directly proportional to Δx. Therefore, we know the force stretching a spring is directly proportional to the distance the spring stretches. If 223 N stretches a spring 12.7 cm, how much stretch can we expect to result from a of 534 N?
- Figure 1 shows a column of fatty tissue, determine the strain in each of the three regions.
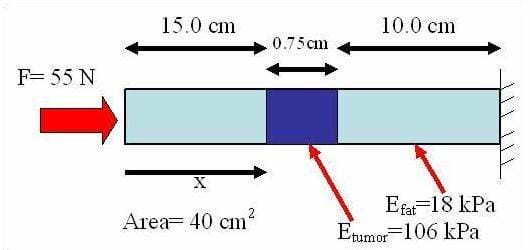
Figure 1. A column of fatty tissue.
Associated Activities
- Applying Hooke's Law to Cancer Detection - Student groups explore Hooke's law by collecting displacement data for springs with unknown spring constants by adding various masses of known weight. After answering a series of application questions, they apply their new understanding to explore a tissue of known surface area. Then then apply the pertinent relationships to depict a cancerous tumor amidst normal tissue by creating a Microsoft Excel® graph.
Vocabulary/Definitions
radiologist: A medical specialist who examines photographs of tissues, organs, bones for use in the treatment of disease.
strain: Deformation of a body or structure as a result of an applied force. Stretch beyond the proper point or limit.
stress: The physical pressure, pull or other force exerted on a system by another. A load, force, or system of forces producing a strain. The ratio of force to area.
Assessment
Post-Introduction Assessment:
Problem Set: Have students complete the Stress, Strain and Hooke's Law Problem Set in class to gauge their comprehension. The final question of the problem set and the application questions from the associated activity serve as an assessment of students' understanding of the challenge. Use these questions as a means of testing whether students are applying their acquired knowledge toward solving the engineering challenge.
Post-Lesson Assessment:
Quiz: Administer the Stress, Strain and Hooke's Law Quiz as a formative post-lesson assessment, serving as part of the Test your Mettle phase of the legacy cycle.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students calculate stress, strain and modulus of elasticity, and learn about the typical engineering stress-strain diagram (graph) of an elastic material.

As part of the engineering design process to create testable model heart valves, students learn about the forces at play in the human body to open and close aortic valves. They learn about blood flow forces, elasticity, stress, strain, valve structure and tissue properties, and Young's modulus, incl...

Students explore Hooke's law while working in small groups at their lab benches. They collect displacement data for springs with unknown spring constants, k, by adding various masses of known weight.

Students are introduced to the concepts of stress and strain with examples that illustrate the characteristics and importance of these forces in our everyday lives. They explore the factors that affect stress, why engineers need to know about it, and the ways engineers describe the strength of mater...
References
Dictionary.com. Lexico Publishing Group,LLC. Accessed December 28, 2008. (Source of vocabulary definitions, with some adaptation) http://www.dictionary.com
Copyright
© 2013 by Regents of the University of Colorado; original © 2007 Vanderbilt UniverityContributors
Luke Diamond; Meghan MurphySupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: April 29, 2020








User Comments & Tips