Lesson Stressed and Strained

Learning Objectives

After this lesson, students should be able to:

• Recognize that engineers use their understanding of forces, stress, strain and material properties to create safe designs for structures, equipment and products.
• Explain how force and area affect stress.
• Distinguish between compression and tension.
• Describe several properties of materials.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Pre-Req Knowledge

Basic understanding of forces such as lift, weight, thrust and drag.

Introduction/Motivation

A man named Robert Hooke described the concept of stress in 1660, and engineers have been using it ever since. For example, engineers analyze how stress affects the chairs we sit in so that the legs are strong enough to not bend or break. Stress analysis is important to keep the wheels on your car and bridges standing up. Materials must be strong enough to withstand the stress upon them. If materials are not strong enough, terrible accidents can happen, such as a floor collapsing because too many people are standing on it! Understanding stress and the strength of materials is very important to keep us safe in our day-to-day lives!

Stress and strength are important parameters for engineers to understand. Stress is a measure of how much force an object experiences per unit area, and strength is a material's ability to withstand stress. When the stress exceeds the strength of a part, it fails. That is what happened in the Hyatt Regency Hotel in Kansas City in 1981, when too many people were dancing on a skyway bridge in the hotel atrium and it collapsed, killing 114 people. Students can conduct the hands-on associated activity Breaking Beams to explore how different designs of homemade clay beams handle stress and affect beam strength. Engineers determine where the stress will be the highest on an object so that part can be redesigned or reinforced. Engineers also specify the materials that objects and structures are made of, so that airplanes can fly safely, wheels do not fall off of automobiles, chairs support the weight of people, bridges support the loads that travel them, and so on.

Lesson Background and Concepts for Teachers

Stress

Stress is a measurement of force spread over area. One way to think of stress is to imagine the different results that happen when a person stands on a trampoline and when a person lays down on a trampoline. A person standing on a trampoline concentrates the force of their weight on a small area and sinks down deeper into the trampoline compared to a person lying down on a trampoline who spreads their force over a larger area, and thus does not sink down as far. A person standing on a trampoline creates a larger stress on the trampoline than a person lying down on it. (See Lesson Extension Activity entitled "Trampoline Forces" to extend this example further). Engineers describe stress mathematically with the equation:

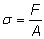
where σ = stress

F = Force [Newtons or lbs]

A = Cross-sectional area [m² or in²]

This equation mathematically tells us the same conclusion as our thought experiment with the trampoline. For a constant force (F), if the area (A) is a small number, the stress (σ) (pronounced "sigma") will be larger. Similarly, if the area is larger, the stress will be smaller.

This mathematical definition is not limited to trampolines. Computing stress works for all sorts of objects experiencing all sorts of different forces. We can compute the stress on objects that are either being compressed or pulled apart. For example, if a rope breaks when a certain force is applied, using a bigger diameter rope will reduce the stress because the cross-sectional area is larger. And, if there is less stress on the rope, it might not break!

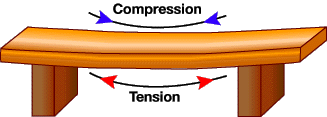
Compressive and Tensile Stresses

Compression occurs when something is being squeezed together. As with the general discussion of stress above, compressive stress is created by forces spread over an area. For example, as you sit in a chair, the legs of the chair are experiencing compressive stresses because they are being squeezed between you and the floor.

On the other hand, tensile stress occurs when something is being pulled apart. A rope in a tug-o-war experiences tensile stress. Ropes can only resist tensile stresses and not compressive stresses, because they are flexible. In other words, you cannot push a rope.

Strain

Strain is a measurement of how an object reacts to stress. Strain is simply a measurement of what the percentage change in an object's shape is when a certain stress is applied to it. A good way to demonstrate strain is with a rubber band. Suppose we have a rubber band that is 100 inches long. Now, we add a tensile stress by hanging a certain amount of weight from the rubber band, which makes it 105 inches long. In this case, the rubber band experienced 5% strain because of the stress created by the weight. Mathematically, strain can be computed by the equation:

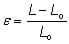
Where ε = strain (percent)

L = new length (mm or in)

L _o = original length (mm or in)

Elastic and Plastic Deformation

When a material is strained, it is said to be deformed. Once a material has been deformed and the stress is relieved, either one of two things will happen: The material goes back to its original shape or the material stays deformed. If the material is able to go back to its original shape, it is called elastically deformed (for example, a rubber band). If the material is strained too much, it will not be able to completely return to its original shape and is called plastically deformed (for example, silly putty).

Properties of Materials — The Big Three

Engineers use their understanding of forces, stress, strain and material properties to create safe designs. We have already discussed forces, stress and strain, so that leaves material properties. Researchers measure properties of materials and how they behave under stress. Yield strength, S_y , is the amount of stress a material can take without plastically (permanently) deforming. If the stress is greater than the yield stress, the material will deform plastically, but not break. Ultimate tensile strength (UTS), S_ut , is the amount of stress a material can take before breaking. The UTS of a material is always greater than or equal to the yield strength. The fatigue strength, S_e , is the stress a material can take one million times over and over again, before breaking. Believe it or not, that seesaw bar will become "tired" after 10 years of use and might give out one day if not designed properly. The fatigue strength is always less than or equal to the yield strength.

So how do engineers use this knowledge? If you were to design a safety rope for rock climbers you would want a rope that would experience stresses less than the S_y and the S_ut . This way, the rope stretches a little to help absorb impact, but does not break. If you were to design playground equipment, you would want to make sure the stresses in the monkey bars were below S_e so that after a million uses they still will not break.

Associated Activities

• Breaking Beams - In this hands-on activity, student explore how different designs of homemade clay beams handle stress and affect beam strength.

  Watch this activity on YouTube

• Team Up! - While completing a team project and learning about the stages of group formation, group dynamics and team member roles, students discover how collective action can foster a sense of community support, which can alleviate personal feelings of stress and tension.

Lesson Closure

Ask the students to explain what engineering stress is and why engineers need to know about stress. Ask the students for different examples of designs that experience stress (bridges, benches, bicycles...this can be just about anything). Ask the students if the stress considerations in these designs are best related to the yield strength, ultimate tensile strength or fatigue strength.

Vocabulary/Definitions

compressive stress: Stress that squeezes a material together.

elastic deformation: Occurs when a material is strained (deformed), but returns to its original shape, like a rubber band.

Fatigue strength: The maximum amount of stress a material can take one million times without breaking.

plastic deformation: Occurs when a material is strained (deformed) beyond its yield strength and does not return to its original shape, like silly putty.

strain: The percent amount of elongation or compression of a material.

stress: The amount of force applied over the area of an object (computed by dividing force by area).

tensile stress: Stress that pulls a material apart.

Ultimate tensile strength: The maximum amount of tensile stress a material can take before breaking.

yield strength: The maximum amount of stress a material can take before it deforms plastically (permanently).

Assessment

Pre-Lesson Assessment

Discussion Questions: Solicit, integrate and summarize student responses to the questions below. Encourage wild ideas and put answers on the board. See Lesson Background section for ideas to suggest if students get stuck.

• What do engineers mean when they talk about "stress?"
• Have you ever experienced something breaking because of the "stress" you put on it?
• How do engineers decide if something is a good design?

Post-Introduction Assessment

Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes and write the totals on the board. Give the right answer.

• True or False: Engineering stress is only the force that is pushing down on something. (Answer: False. Engineering stress is a force on an object in any direction. It is also any pulling force as well as any pushing force.)
• True or False: A rope can feel stress. (Answer: True. A rope can feel stress when it is pulled. This is called tensile stress.)
• True or False: Engineers think about the stress of a plastic when designing new toys. (Answer: True. Engineers try to design toys that will not break easily.)
• True or False: The chair you are sitting on has very little strength. (Answer: False. If the chair legs had little strength, the chair would break and you would fall.)

Vocabulary: Ask the students to write down the vocabulary words and definitions on a sheet of paper or in their science journals.

Lesson Summary Assessment

Bingo: Provide each student with a sheet of paper to draw a large tic-tac-toe board (a 3 x 3 grid with 9 squares) that fills the entire paper. Have the students write a lesson vocabulary term in each square (there are enough vocabulary words to fill up the nine squares). Next, have each student walk around the room and find a student who can accurately define one vocabulary term. Students must find a different student for each term. When a student has all terms completed they shout "Bingo!" Continue until two or three students have bingo. Ask the students who shouted "Bingo!" to give definitions of the vocabulary terms.

Using the Equations: Ask students to solve the following practice problems using the equations from the Lesson Background:

• A metal wire has a 2.5 mm diameter and is 2000 mm long. A force of 12 N is applied to it, causing it to stretch 0.3 mm. Assuming the material is elastic, determine the stress and strain in the wire. (Hint: the cross-sectional area is 4.909 mm²) [Answer: σ = F/A =12 N / 4.909 mm² = 2.44 N/mm². ε = (L-L₀)/L₀ = 0.3 mm / 2000 mm = 0.00015]
• Given a strain of 0.0025 and an original length of 1000 mm, find the new length of the wire. (Answer: L= ε* L₀ + L₀ = 0.0025*1000 mm + 1000 mm = 1002.5 mm)

Lesson Extension Activities

Have the students find an object in the room (or at home, in the case of a homework assignment) that demonstrates each one of the vocabulary words.

Have the students write a fictional story about stress and strain that includes all of the vocabulary words.

Have the students research different specific examples of when engineering failed in terms of stress and strain. (For example, structures that collapsed during earthquakes or hurricanes, bridges that were affected by high winds, space structures that failed due to a lack of gravity, etc.) What did engineers have to do to fix each situation? Have them create a poster about the example and include a discussion of the incident in terms if materials, stress and strain.

Have the students research three types of bridges. How do these bridges compare and contrast to each other? How does each bridge deal with compression and tension forces?

Trampoline Forces: Extend the conversation about trampolines from the lesson. "One way to think of stress is to imagine the different results that happen when a person stands on a trampoline and when a person lays down on a trampoline. A person standing on a trampoline concentrates the force of their weight on a small area and sinks down deeper into the trampoline compared to a person lying down on a trampoline who spreads their force over a larger area, and thus does not sink down as far. A person standing on a trampoline creates a larger stress on the trampoline than a person lying down on it." This example applies to a person that is standing still on the trampoline. Now imagine that the person (we will call them Person A) begins jumping up and down. In groups of two, do your best to answer the following questions based on this scenario:

1. As Person A is jumping on the trampoline, what forces are acting on them? [Answer: downward force of gravity, upward force from the trampoline, students might mention air friction].
2. Now think about how these forces sum to influence the changing motion of Person A on the trampoline. Specifically, think about these three main stages of Person A's motion: (a) Person A flying upwards, (b) the second just before Person A starts to come back down, and (c) Person A falling back down to the trampoline. Compare the forces you described in #1 and how they are enabling Person A to either move up, stay still in the air, or move down. [Answer: The most important aspect for students to grasp is that when Person A is moving upward, the force from the trampoline provided an upward velocity that is overcoming the downward gravitational force, however Person A is slowing down because gravity is acting on them. Once gravity has slowed Person A's velocity down to 0 (at their maximum height), gravity then acts to accelerate Person A downwards back to the trampoline].
3. Upon impact, does the trampoline experience more stress than when Person A was standing still? Why or why not? Use the stress equation to explain your answer qualitatively. [Answer: More stress because the force exerting on the trampoline is greater, even though the area is the same].

References

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.