Summary
As part of the engineering design process to create testable model heart valves, students learn about the forces at play in the human body to open and close aortic valves. They learn about blood flow forces, elasticity, stress, strain, valve structure and tissue properties, and Young's modulus, including laminar and oscillatory flow, stress vs. strain relationship and how to calculate Young's modulus. They complete some practice problems that use the equations learned in the lesson—mathematical functions that relate to the functioning of the human heart. With this understanding, students are ready for the associated activity, during which they research and test materials and incorporate the most suitable to design, build and test their own prototype model heart valves.Engineering Connection
Materials are an important aspect of new technology and new product designs created by engineers. When biomedical engineers design objects and devices to serve as replacement parts and organs in the human body, materials are especially important because the artificial parts must reliably perform inside living people. So, engineers study and analyze real body parts, such as heart valve tissue, in order to understand their structures, properties and behavior. They also research and test (and sometimes design new) materials that are suitable to fabricate artificial parts that function as close as possible to real parts. To do this, they determine the forces that body parts must withstand in the body, how the tissues respond, and other factors and measured characteristics such as stress, strain, elasticity and Young's modulus.
Learning Objectives
After this lesson, students should be able to:
- Describe the forces encountered in the human body to open and close aortic valves.
- Define Young's modulus and how it relates to the properties of valve tissues.
- Determine the Young's modulus for a material by calculating the materials' stress and strain and creating a stress vs. strain graph.
- Calculate Young's modulus for various materials and use the Young's modulus, stress and strain equations to calculate unknown values, such as force.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-1. Analyze a major global challenge to specify qualitative and quantitative criteria and constraints for solutions that account for societal needs and wants. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Analyze complex real-world problems by specifying criteria and constraints for successful solutions. Alignment agreement: | Criteria and constraints also include satisfying any requirements set by society, such as taking issues of risk mitigation into account, and they should be quantified to the extent possible and stated in such a way that one can tell if a given design meets them. Alignment agreement: Humanity faces major global challenges today, such as the need for supplies of clean water and food or for energy sources that minimize pollution, which can be addressed through engineering. These global challenges also may have manifestations in local communities.Alignment agreement: | New technologies can have deep impacts on society and the environment, including some that were not anticipated. Analysis of costs and benefits is a critical aspect of decisions about technology. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-2. Design a solution to a complex real-world problem by breaking it down into smaller, more manageable problems that can be solved through engineering. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | Criteria may need to be broken down into simpler ones that can be approached systematically, and decisions about the priority of certain criteria over others (trade-offs) may be needed. Alignment agreement: | |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-LS1-2. Develop and use a model to illustrate the hierarchical organization of interacting systems that provide specific functions within multicellular organisms. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop and use a model based on evidence to illustrate the relationships between systems or between components of a system. Alignment agreement: | Multicellular organisms have a hierarchical structural organization, in which any one system is made up of numerous parts and is itself a component of the next level. Alignment agreement: | Models (e.g., physical, mathematical, computer models) can be used to simulate systems and interactions—including energy, matter, and information flows—within and between systems at different scales. Alignment agreement: |
Common Core State Standards - Math
-
Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret the slope (rate of change) and the intercept (constant term) of a linear model in the context of the data.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Medical technologies include prevention and rehabilitation, vaccines and pharmaceuticals, medical and surgical procedures, genetic engineering, and the systems within which health is protected and maintained.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Design problems are seldom presented in a clearly defined form.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Technological problems must be researched before they can be solved.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Tennessee - Science
-
Explore the anatomy of the heart and describe the pathway of blood through this organ.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Describe the biochemical and physiological nature of heart function.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Explain the relationship between the properties of a material and the use of the material in the application of a technology.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Graph relationships and functions between manipulated (independent) variables and responding (dependent) variables.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Determine the slope of a linear function.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_floppy_lesson02] to print or download.Pre-Req Knowledge
Students should have an understanding of:
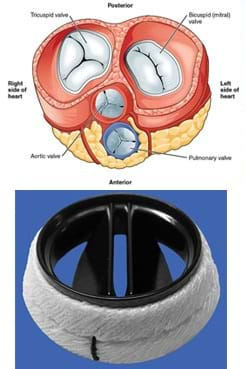
- Heart anatomy, heart valve structure and how heart valves, specifically the aortic valve, function, such as presented in the What Do I Need to Know about Heart Valves? previous lesson and its associated activity.
- Graphing data with Microsoft Excel® (or similar software application) to make line graphs or scatter plots and determining a line of best fit and its equation.
- Given an equation of a line, identify the slope.
Introduction/Motivation
(In advance, make copies of the Heart Functioning Pre-Test; Forces, Elasticity, Stress, Strain and Young's Modulus Handout; and Young's Modulus Practice Problems, one each per student. Administer the pre-test before beginning the lesson to verify student understanding of the concepts.)
At this point in our unit, we have learned all about the heart and even dissected real (sheep) hearts. We have also discussed the specific anatomy of aortic valves and how they function. Now, we need to focus on designing model heart valves. The materials we use for model heart valves need to represent the organic tissue that composes real heart valves, so first it is important that we learn about how blood flows through the valves and the forces exerted on the valves, as well as the elasticity of the valves.
Lesson Background and Concepts for Teachers
The following information is provided as a lecture guide; it is also on the student handout, which you may want to give to students at the beginning of the lesson. Once the lesson's content on forces, elasticity, stress, strain, valve structure and tissue properties, and Young's modulus is covered with students, distribute the practice problems so they can reinforce the concepts on their own. Following the lesson, have students reinforce their learning with the Does My Model Valve Stack up to the Real Thing? activity where they research, test and select suitable materials that best mimic heart valve tissue with their own prototype.
Lesson Schedule
- Administer the pre-test.
- Students learn about the specific forces exerted on heart valves as blood flows through vessels, as well as information about tissue elasticity, via lecture and a handout.
- Students complete practice problems to solidify their understanding of Young's modulus and the concepts presented.
Forces Exerted on the Aortic Valve during Blood Flow
When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to "relax," permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see Figure 1).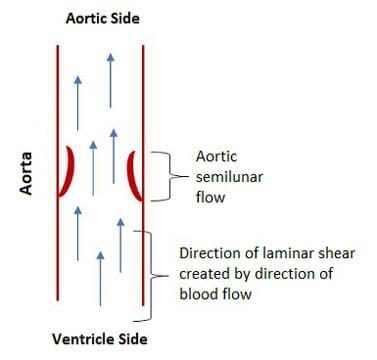
During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see Figure 2); this flow is oscillatory in nature.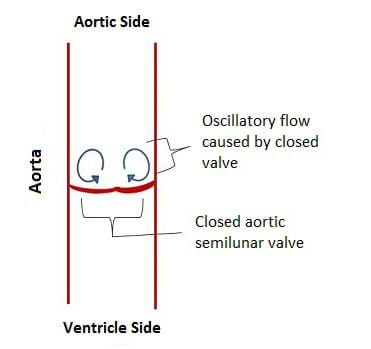
Elasticity and Young's Modulus
Elasticity describes a material property in which the material returns to its original shape after stress has been applied and then removed. When thinking about elasticity, think about a coiled metal spring or a rubber band. Imagine applying stress to a rubber band by pulling on it. Once the stress is removed (you stop pulling on it), the rubber band recoils to its original shape. The exception to this when too much stress is applied to the rubber band, causing permanent deformation (the rubber band breaks or does not return to its original shape).
So, what is stress? In this situation, stress is an amount of force applied to an object. The stress applied to the rubber band temporarily changes its shape, until the stress is removed.
All materials experience some change with the application of force. However, different materials respond differently to stress. For example, a steel beam reacts differently to stress than a bungee cord. A measurement of the elasticity of a material is called the Young's modulus, and is determined as a ratio of stress to strain:
Young's modulus (Y) = stress/strain
Young's modulus can be used in the following equation:
F = Y(∆L/L0)A
In this equation, F is equal to the force applied to the structure, Y is the Young's modulus for the material, ΔL is the change in length of the material when the force is applied to it, L0 is the initial length, and A is the cross-sectional area of the material.
Example Young's modulus for some different materials:
- Pig heart valve: 1.2 X 106 Pascal (Pa)
- Rubber: 1.0 X 108 Pa
- Tooth enamel: 8.3 X 109 Pa
- Steel: 2.0 X 1011 Pa
- Carbon nanotube: 1.0 X 1012 Pa
Young's Modulus Practice Problem
As a class, go through the following practice problem, writing each step on the classroom board.
Problem: A steel cable with an initial length of 20 meters and a diameter of .05 m suspends an elevator car in its shaft. Three people, having a total mass of 238 kg, enter the elevator car. Given the elevator cable is made of steel, what is the amount of stretch that the cable experiences when the three passengers enter the elevator?
Solution: We already know:
L0 = 20 m (given)
Y = 2 X 1011 Pa = 200000000000 Pa (given)
A = πr2 = 3.14(.025 m)2 = .002 m2 (using given diameter of .05 m)
F = ma = 238 kg X 9.8 m/s2 = 2332 N (using given mass of people and the Earth's gravitational acceleration)
ΔL = unknown
Using what we know, we can do the following calculations:
F = Y(∆L/L0)A
2332 N = (200000000000 Pa) (x/20 m) (.002 m2)
2332 = (x/20) (400000000)
0.0000058 = (x/20)
0.00012 = x
Thus, the cable will stretch .00012 m (or .12 mm) when the three passengers enter the elevator.
Stress and Strain
Stress (force divided by cross-sectional area) can be expressed as: σ= F/A
Strain (change in length divided by initial length) can be expressed as: ɛ=∆L/L0
Remember the equation covered earlier: F = Y(∆L/L0)A
This equation can be rewritten by dividing both sides by A to look like: F/A= Y(∆L/L0)
This shows that stress (F/A) is proportional to strain (ΔL/L0 ), in the elastic region of the stress/strain curve, and can thus be graphed. When these are graphed, with the stress on the y-axis and the strain on the x-axis, the slope of the resulting best-fit line is equal to the Young's modulus of the material (see Figure 3).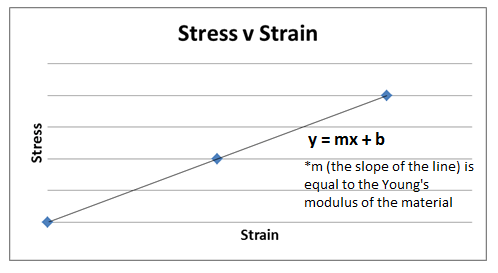
Associated Activities
- Does My Model Valve Stack up to the Real Thing? - As a culminating activity of the Floppy Heart Valves unit, student teams apply their newly gained knowledge about heart valves to research, test and select suitable materials that best mimic heart valve tissue, design and build prototype valve models, test and make modifications to their models, and then make written and verbal presentations of their model heart valve solutions to the unit's engineering design challenge.
Lesson Closure
What have you learned in this lesson? (Listen to student responses.) You have learned about aortic valve structure and tissue properties and behavior, and the forces heart valves encounter due to blood flow (stress, strain, laminar and oscillatory flow). You have learned about elasticity and how to calculate Young's modulus. Whew! Your understanding of the mathematical functions that relate to the functioning of the human heart will help you to design a solution for the unit's engineering challenge problem.
Why do biomedical engineers care so much about the materials they use in their designs for replacement body parts? (Listen to student ideas.) That's right. The devices and parts they design need to work reliably because peoples' health depends on it, and the new parts often reside inside a body, so the materials must function in those conditions. How do they figure this out? (Listen to student ideas.) Well first they research heart valve anatomy and function, and then research to find (and sometimes design new) materials that are suitable to fabricate artificial replacement valves. Once appropriate materials have been identified, they develop valve designs that mimic the function of real valves. To help ensure that artificial valves are as close to their natural analogues, the materials must have similar properties and behavior to real heart valve tissue.
In the coming activity, your goal is to determine what materials to use for your model heart valves, so you will gather information on heart valve tissue properties, test possible materials, and then design and create prototypes and make modifications to them, so that they behave similarly to real heart valves. Your final task is to pull together all of the information that you have learned into a portfolio presentation for your client to examine before they start using your models.
Vocabulary/Definitions
deformation: A permanent change in the shape when excess stress is put on a material.
elasticity: A material property in which it returns to its original shape after stress has been applied and removed.
laminar flow: A smooth flow of fluid; a streamline flow.
recoil: The action of a material moving back to its original shape after stress is removed.
strain: The amount a material stretches compared to its initial size, in response to stress placed on it.
stress: The amount of force per unit area applied to a material.
Young's modulus: A measure of the stiffness of a material; a ratio of the stress applied to the material to the strain (deformation) of the material. Every material has a specific modulus.
Assessment
Pre-Lesson Assessment
Pre-Test: Administer the four-question Heart Functioning Pre-Test at the beginning of the lesson. The pre-test reviews the functions and locations of the aorta and the aortic valve, and asks students to consider the forces that act on these organs due to blood flow. Students must understand these concepts before starting the lesson.
Lesson Summary Assessment
Practice Problems: Have students complete the Young's Modulus Practice Problems to assess their ability to calculate Young's modulus using the equations presented in the lesson. Question 2 asks them to create a Microsoft Excel® graph of the provided data (four data points), but the graph may be created by hand as well. Review their work to assess their comprehension of the lesson concepts.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to Hooke's law as well as stress-strain relationships. Through the lesson's two-part associated activity, students 1) explore Hooke's law by experimentally determining an unknown spring constant, and then 2) apply what they've learned to create a strain graph depicting a tumo...

Students are presented with the unit's grand challenge problem: You are the lead engineer for a biomaterials company that has a cardiovascular systems client who wants you to develop a model that can be used to test the properties of heart valves without using real specimens.

Students calculate stress, strain and modulus of elasticity, and learn about the typical engineering stress-strain diagram (graph) of an elastic material.

Students learn how healthy human heart valves function and the different diseases that can affect heart valves. They also learn about devices and procedures that biomedical engineers have designed to help people with damaged or diseased heart valves.
References
Campbell, N., Reece, J., Urry, L., Cain, M., and Wasserman, S. Biology. Eighth edition. San Francisco, CA: Benjamin-Cummings Publishing Co., 2007.
Nagatomi, Jiro. Mechanobiology Handbook. Boca Raton, FL: CRC Press, 2011.
Copyright
© 2013 by Regents of the University of Colorado; original © 2012 Vanderbilt UniversityContributors
Michael DuplessisSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: June 6, 2019









User Comments & Tips