Quick Look
Grade Level: 11 (10-12)
Time Required: 1 hours 15 minutes
Expendable Cost/Group: US $0.00 The activity requires some non-expendable (reusable) computers and lab equipment; see the Materials List for details.
Group Size: 3
Activity Dependency:
Subject Areas: Physical Science, Physics
Summary
Students explore Hooke's law while working in small groups at their lab benches. They collect displacement data for springs with unknown spring constants, k, by adding various masses of known weight. After exploring Hooke's law and answering a series of application questions, students apply their new understanding to explore a tissue of known surface area. Students then use the necessary relationships to depict a cancerous tumor amidst normal tissue by creating a graph in Microsoft Excel.Engineering Connection
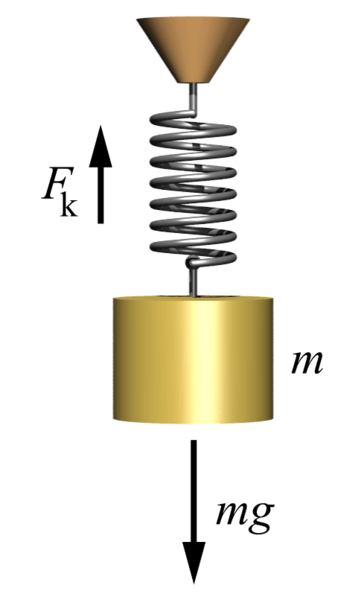
Hooke's law defines the direct proportionality between a spring's deformation and the restoring force that results. Most commonly, a derivative of Hooke's law is used in engineering applications—a relationship that directly relates stress and strain. For example, the stress-strain curve is commonly used by material scientists and engineers while selecting materials for structures. Within the linear region, the slope is defined by the Young's modulus of elasticity. Civil engineers often study the stress-strain curve when using strain hardening and other methods to increase the yield strength of a material. In this activity, particularly in the investigating questions 6 and 7, students explore the relationship between Hooke's law and the stress-strain equation. In addition, students must apply their understanding of Hooke's law to create a strain plot.
Learning Objectives
After this activity, students should be able to:
- Describe what is meant by Hooke's law.
- Apply Hooke's law relationships to analyzing tissue of a known surface area.
- Depict a cancerous tumor using graphing methods in Microsoft Excel.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Analyze data using tools, technologies, and/or models (e.g., computational, mathematical) in order to make valid and reliable scientific claims or determine an optimal design solution.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Theories and laws provide explanations in science.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Laws are statements or descriptions of the relationships among observable phenomena.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Use mathematical or computational representations of phenomena to describe explanations.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
Common Core State Standards - Math
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Look for and make use of structure.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Fit a linear function for a scatter plot that suggests a linear association.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret the slope (rate of change) and the intercept (constant term) of a linear model in the context of the data.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Fit a function to the data; use functions fitted to data to solve problems in the context of the data.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Use computers and calculators to access, retrieve, organize, process, maintain, interpret, and evaluate data and information in order to communicate.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use various approaches to communicate processes and procedures for using, maintaining, and assessing technological products and systems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Tennessee - Math
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Look for and make use of structure.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Fit a linear function for a scatter plot that suggests a linear association.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret the slope (rate of change) and the intercept (constant term) of a linear model in the context of the data.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Fit a function to the data; use functions fitted to data to solve problems in the context of the data.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Tennessee - Science
-
Solve problems related to velocity, acceleration, force, work, and power.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Part 1:
Each lab group needs:
- physics lab stand
- meter stick
- spring (with hooks)
- pendulum clamp
- slotted mass set
- computer with Microsoft Excel (or other spreadsheet application)
- Hooke's Law Worksheet, one per student
Part 2:
Each group needs a computer with Microsoft Excel and the Generating a 1-D Strain Plot Handout. The handout has instructions specifically for Excel, but if you adjust the instructions, another spreadsheet program could be used.
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/van_cancer_activity2] to print or download.Pre-Req Knowledge
A basic understanding of the concepts of Hooke's law, stress and strain, as presented in Lesson 2.
Introduction/Motivation
Have you ever wondered how the value of the gas constant was measured/discovered, or the charge on an electron, or the Young's modulus of elasticity values we used in the problem set yesterday? Ever wondered where all these values come from? Well today we are going to solve for one ourselves.
In groups of three, we are going to experimentally find the spring constant, k, for a few springs. After collecting data, we will use the relationship given by Hooke's law to solve for an approximation of the constant.
After exploring Hooke's law and answering a few application questions, we will apply what we've learned to study a body tissue with known surface area. Because Hooke's law applies to springs, we must make a few adaptations to the expression F= -k Δx, to account for area. By the end of the activity, you will be able to apply what you know about Hooke's law, stress and strain to depict a tumor amidst normal tissue using a graph in Microsoft Excel.
Procedure
Background
This activity constitutes the Research and Revise phase of the legacy cycle. Students explore Hooke's law in a hands-on, laboratory situation. They experimentally solve for the spring constant, k, of a given spring by measuring the spring's displacement when a mass of known weight is added. After answering some application questions on Hooke's law, students relate Hooke's law to a body tissue of known surface area. Continuing their research and revising their initial thoughts for solving the engineering challenge, students follow step-by-step instructions to depict a cancerous tissue in a graph generated in Microsoft Excel. Though students work in groups, it is expected that they complete their own activity worksheets. Students may discuss the questions but should answer the questions individually.
Before the Activity
- Provide each lab station with the necessary materials.
- Assign groups of three for the activity.
- Make copies of the Hooke's Law Worksheet and Generating a 1-D Strain Plot Handout.

Example lab setup.
With the Students
- Pass out the two handouts. Use the Hooke's Law Worksheet as an instructional guide when creating strain plots. Use the Generating a 1-D Strain Plot Handout as an instructional guide to the lab; each student is responsible for completing and submitting the analysis and application questions by the end of the class period.
- Have students move into their assigned groups and go to their lab benches.
- Direct students to follow the worksheet and handout instructions. Remind them that they may work together, but each student is responsible for completing and turning in their own answers and solutions.
- When students are ready to move on to the strain plot, have them remain in their groups; only one graph needs to be turned in per group. Remind them to return to their initial thoughts notes and add any new notes that may help them solve the challenge.
Vocabulary/Definitions
cancer: A malignant and invasive growth or tumor tending to recur after removal and to metastasize to other sites.
force: An influence on a body or system, producing a change in movement or in shape or other effects.
spring: An elastic body such as a wire of steel coiled spirally that recovers its shape after being compressed, bent or stretched.
strain: Deformation of a body or structure as a result of an applied force beyond limit.
stress: The physical pressure, pull or other force exerted on a system by another, producing a strain. Measured by the ratio of force to area.
ultrasound imaging: The application of ultrasonic waves to therapy or diagnostics, as in deep-heat treatment of a joint or imaging of internal structures.
Young's modulus of elasticity: A mathematical constant that represents how difficult a material is to stretch
Assessment
Activity Embedded Assessment: The Hooke's law application questions and the 1-D strain plot both function as means of assessment. Students must first develop an understanding of Hooke's law. Then they must relate this concept to a tissue with known cross-sectional area. This concept may be used to detect a cancerous tumor where the tumor's elastic properties differ from that of normal tissue.
Investigating Questions
- How does Hooke's law and the stress-strain relationship relate? Which variables correspond?
- What do we know about cancerous tissue that allows us to use these concepts to depict it?
- What types of software would be appropriate for our imaging?
- Using these methods, will our imaging method be painless? Will it be effective and reliable? How about cost effective?
Activity Extensions
To extend the hands-on aspect of exploring the tissue, consider obtaining ballistic gel (such as https://en.wikipedia.org/wiki/Ballistic_gelatin) of differing stiffness. This may be used to mimic the differing tissue structure of cancerous and normal tissue as represented by varying Young's modulus of elasticity.
Activity Scaling
- For upper-level students, remove the step-by-step instructions for generating the 1-D strain plot.
- For lower-level students, take the time to relate Hooke's law to the stress-strain relationship as a class. Make this connection with the students, using a visual representation on the board.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to Hooke's law as well as stress-strain relationships. Through the lesson's two-part associated activity, students 1) explore Hooke's law by experimentally determining an unknown spring constant, and then 2) apply what they've learned to create a strain graph depicting a tumo...

Students calculate stress, strain and modulus of elasticity, and learn about the typical engineering stress-strain diagram (graph) of an elastic material.

In addition to the associated lesson, this activity functions as a summative assessment for the Using Stress and Strain to Detect Cancer unit. In this activity, students create 1-D strain plots in Microsoft Excel® depicting the location of a breast tumor amidst healthy tissue.

Students are presented with a biomedical engineering challenge: Breast cancer is the second-leading cause of cancer-related death among women and the American Cancer Society says mammography is the best early-detection tool available. This three lesson/three activity unit provides hands-on activitie...
References
Dictionary.com. Lexico Publishing Group,LLC. Accessed December 28, 2008. (source of vocabulary definitions, with some adaptation)
Copyright
© 2007 by Regents of the University of Colorado; original © 2007 Vanderbilt UniversityContributors
Luke Diamond; Meghan MurphySupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: January 16, 2020







User Comments & Tips