Hands-on Activity Measuring Viscosity

Learning Objectives

After this activity, students should be able to:

• Measure the viscosity of a fluid.
• Describe a fluid as having "high" or "low" viscosity.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• ruler
• stopwatch
• graduated cylinder (the taller the better)
• marble or steel ball (must be half the diameter of the cylinder or smaller, and sink in the fluid being measured; the slower the ball sinks, the easier it is to measure the viscosity)
• Viscosity Activity Worksheet, one per person
• calculators
• Internet access, to research viscosities for one worksheet question

To share with the entire class:

• thick, somewhat clear household fluids, such as motor oil, corn syrup, pancake syrup, shampoo, liquid soap (perhaps a different fluid for each 1-2 groups), enough of each liquid to fill a graduated cylinder for each group that tests it
• scale, to measure the masses of graduated cylinders, with and without the liquids

Worksheets and Attachments

Introduction/Motivation

Fluid mechanics is the study of how fluids react to forces. Fluid mechanics includes hydrodynamics, the study of force on liquids, and aerodynamics, the study of bodies moving through air. This encompasses a wide variety of applications. Can you think of any examples of engineering applications for which an understanding the behavior of fluids is important? (Listen to student ideas.) Environmental engineers use fluid mechanics to study pollution dispersion, forest fires, volcano behavior, weather patterns to aid in long-term weather forecasting, and oceanography. Mechanical engineers implement fluid mechanics when designing sports equipment such as golf balls, footballs, baseballs, road bikes and swimming gear. Bioengineers study medical conditions such as blood flow through an aneurysm. Aerospace engineers study gas turbines that launch space shuttles and civil engineers use fluid mechanics for dam design. Considering just these few examples of the wide variety of applications of fluid mechanics, you can see how fluid mechanics is important to understand for many types of engineering design in our world.

In this activity, we'll be measuring a property of fluids called viscosity. Viscosity describes how a fluid resists forces, or more specifically shear forces. Shear is the type of force that occurs when two objects slide parallel to one another. Since fluids are composed of many molecules that are all moving, these molecules exert a shear force on one another. Fluids with low viscosity have a low resistance to shear forces, and therefore the molecules flow quickly and are easy to move through. Can anyone name an example of a low-viscosity fluid? (Listen to student ideas.) One example is air! Another example is water. Fluids with high viscosity flow more slowly and are harder to move through. What are examples of high-viscosity fluids? (Listen to student ideas). One example of a high-viscosity fluid is honey.

When an object free falls through a fluid, at some point the force due to gravity is balanced by the resistance to shear by the fluid. This is called terminal velocity, and is the point at which the falling object maintains a constant velocity. Skydivers enjoy one terminal velocity when they are in free-fall and another, much slower terminal velocity when they change their shape by releasing their parachutes.

For objects that have simple geometries, such as spheres, the drag on the object can be calculated with known equations. Because of this, engineers can calculate the terminal velocity of a sphere falling through a known fluid using the following equation: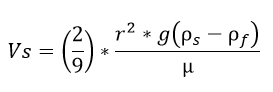

where g is acceleration due to gravity, ρ_s is the density of the sphere, ρ_f is the density of the fluid, μ (mu) is the viscosity of the fluid, and V_s is the terminal velocity of the sphere. Why do you think this might be useful? (Listen to student ideas.) Some examples might be: Calculating free-fall velocity of a skydiver, or calculating the velocity of a spaceship in re-entry. Using algebra, the equation can be re-arranged in order to calculate the viscosity of an unknown fluid falling at a known terminal velocity: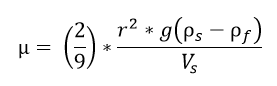

Being able to re-arrange equations to find the unknowns is an important skill for engineers! In this activity, we will measure the viscosities of a few household fluids by dropping balls into them and measuring the terminal velocities.

Procedure

Before the Activity

• Gather materials and make copies of the Viscosity Activity Worksheet.
• Be sure the ball sinks slowly enough in all of the fluids that a velocity measurement can be obtained. If the ball falls too quickly, it is hard to accurately start and stop the stopwatch.
• Divide the class into groups of three students each. Hand out the worksheets.

With the Students

1. Have each group choose a fluid to measure the viscosity of (or assign each group a fluid).
2. Have students calculate the density of the fluid.

• Weigh the empty graduated cylinder.
• Fill the cylinder with fluid, and record the volume.
• Weigh the full graduated cylinder. Subtract the mass of the empty graduated cylinder to determine the mass of the fluid.
• The density of the fluid is the mass over the volume.

  

Note: 1 cm³=1 ml.

3. Have students measure the density of the sphere.

• Measure the radius of the ball. Record as r [cm].
• Calculate the volume of the sphere:

  

Alternatively, place the sphere in a graduated cylinder half filled with water; the displacement of the water is equal to the volume of the sphere.

• Weigh the sphere, and calculate the density:

  

4. Have students drop the ball into the fluid, timing the ball as it falls a measured distance.

(Note: Ideally students would wait for the ball to reach a constant velocity, however for this activity we assume the ball reaches terminal velocity very quickly, so that students can measure the time from when the ball enters the fluid until it reaches the cylinder bottom. For less-viscous, "thinner," fluids, this may be very quick).

5. Calculate the velocity of the ball falling through the fluid.

   

6. Calculate the viscosity of the fluid using the following equation,

   

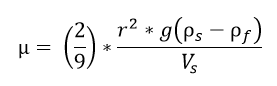
where g is acceleration due to gravity (981 [cm/s²]). The answer should be in units of kg/cm s, or mPa-s. For comparison, the viscosity of water is approximately 1 mPa-s.

7. For accuracy, have students repeat the experiment and calculate an average viscosity.
8. Have groups share, compare and discuss their results as a class by either writing the results in a table on the board or on a class overhead projector.

Vocabulary/Definitions

shear: A type of force that occurs when two objects slide parallel to one another.

terminal velocity: The point at which the force exerted by gravity on a falling object is equaled by a fluid's resistance to that force.

viscosity: A fluid's ability to resist forces.

Assessment

Pre-Activity Assessment

Discussion Questions: Considering the fluids available for activity testing, ask students to estimate which liquid they think will have the highest viscosity. Which will have the lowest? Write their predictions on the board.

Activity Embedded Assessment

Worksheet: Have students complete the Viscosity Activity Worksheet during the activity. If time is limited, have them research online for viscosities of common household fluids (last question) as a homework assignment. Review their answers to gauge their comprehension of the subject matter.

Post-Activity Assessment

Graphing: Have students plot fluid density (independent) vs. viscosity (dependent). In addition, students could compare marbles of various diameters and describe patterns between fluid density and viscosity, and between fluid density and marble diamater. Students then determine if the model is linear, quadratic, or exponential; if linear, use the two-point method to determine the line of best fit.

Class Presentation: Have students share and discuss their measured/calculated viscosities with the class. Compare and discuss the class results with the predictions made before beginning the activity.

Safety Issues

• Do not allow students to drink the test fluids, especially after the fluids have been in contact with the graduated cylinders.
• After the activity, responsibly dispose of the used test fluids.
• Shampoo or dish soap may create a large amount of suds when cleaning the graduated cylinders.

Troubleshooting Tips

If the marble falls too quickly through the fluid to obtain accurate timing, use a taller graduated cylinder or a lighter marble (or both!).

Activity Extensions

Viscosity changes with temperature! Have students measure the viscosity of a fluid at a few different temperatures and graph the viscosity (y-axis) vs. temperature (x-axis).

Activity Scaling

• For lower grades, just visually compare the times it takes the balls to fall through the fluids. Perhaps a viscosity race!
• For upper grades, try varying the temperature of a fluid (see the Activity Extension section).

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of these digital library curricula were developed by the Integrated Teaching and Learning Program under National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.