Quick Look
Grade Level: 8 (8-10)
Time Required: 45 minutes
Expendable Cost/Group: US $3.00 This activity requires the use of non-expendable (reusable) LEGO® MINDSTORMS® NXT robot kits, one per group ($490 each); see the Materials List for details.
Group Size: 5
Activity Dependency: None
Subject Areas: Physics, Science and Technology
NGSS Performance Expectations:

| HS-PS2-1 |
| MS-ETS1-4 |
| MS-PS2-2 |

Summary
Students work as physicists to understand centripetal acceleration concepts. They also learn about a good robot design and the accelerometer sensor. They also learn about the relationship between centripetal acceleration and centripetal force—governed by the radius between the motor and accelerometer and the amount of mass at the end of the robot's arm. Students graph and analyze data collected from an accelerometer, and learn to design robots with proper weight distribution across the robot for their robotic arms. Upon using a data logging program, they view their own data collected during the activity. By activity end, students understand how a change in radius or mass can affect the data obtained from the accelerometer through the plots generated from the data logging program. More specifically, students learn about the accuracy and precision of the accelerometer measurements from numerous trials. **Note: This activity uses the retired LEGO NXT robot which is no longer available for purchase.Engineering Connection
Understanding centripetal forces is important for engineers who design devices that follow curved paths, such as airplanes, satellites, space ships, cars and amusement park rides. The key factors that affect centripetal force and acceleration—mass, radius and velocity—all play important roles in how engineers design equipment that is counted on to work correctly and safely every day, all over the world. Civil engineers apply their understanding of centripetal acceleration to design highways that are safe for cars traveling at high speeds. Other engineers apply their understanding of centripetal acceleration to make sure that satellites follow the right path and accurately provide people with directions via GPS.
Learning Objectives
After this activity, students should be able to:
- Describe the parts of a robot.
- Design a LEGO-based arm.
- Explain how data logging works, as well as how to acquire data from data logging and record that data using sensors.
- Program a robot with LEGO MINDSTORMS NXT software.
- Understand how to program an accelerometer and monitor it in data logging.
- Know how to manipulate the mass and radius of the accelerometer.
- Accurately monitor the change in acceleration when the mass on the arm and the radius from the motor to the accelerometer are changed.

Figure 2. Accelerometer sensor on a robotic arm, used to monitor tilt across three axes.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-1. Analyze data to support the claim that Newton's second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Analyze data using tools, technologies, and/or models (e.g., computational, mathematical) in order to make valid and reliable scientific claims or determine an optimal design solution. Alignment agreement: Theories and laws provide explanations in science.Alignment agreement: Laws are statements or descriptions of the relationships among observable phenomena.Alignment agreement: | Newton's second law accurately predicts changes in the motion of macroscopic objects. Alignment agreement: Attraction and repulsion between electric charges at the atomic scale explain the structure, properties, and transformations of matter, as well as the contact forces between material objects.Alignment agreement: | Empirical evidence is required to differentiate between cause and correlation and make claims about specific causes and effects. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ETS1-4. Develop a model to generate data for iterative testing and modification of a proposed object, tool, or process such that an optimal design can be achieved. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop a model to generate data to test ideas about designed systems, including those representing inputs and outputs. Alignment agreement: | Models of all kinds are important for testing solutions. Alignment agreement: The iterative process of testing the most promising solutions and modifying what is proposed on the basis of the test results leads to greater refinement and ultimately to an optimal solution.Alignment agreement: | |
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS2-2. Plan an investigation to provide evidence that the change in an object's motion depends on the sum of the forces on the object and the mass of the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan an investigation individually and collaboratively, and in the design: identify independent and dependent variables and controls, what tools are needed to do the gathering, how measurements will be recorded, and how many data are needed to support a claim. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | The motion of an object is determined by the sum of the forces acting on it; if the total force on the object is not zero, its motion will change. The greater the mass of the object, the greater the force needed to achieve the same change in motion. For any given object, a larger force causes a larger change in motion. Alignment agreement: All positions of objects and the directions of forces and motions must be described in an arbitrarily chosen reference frame and arbitrarily chosen units of size. In order to share information with other people, these choices must also be shared.Alignment agreement: | Explanations of stability and change in natural or designed systems can be constructed by examining the changes over time and forces at different scales. Alignment agreement: |
Common Core State Standards - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret expressions that represent a quantity in terms of its context
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the effects of technology on the environment.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the role of society in the development and use of technology.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the role of troubleshooting, research and development, invention and innovation, and experimentation in problem solving.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret expressions that represent a quantity in terms of its context
(Grades
9 -
12)
More Details
Do you agree with this alignment?
New York - Science
-
Develop a model to generate data for iterative testing and modification of a proposed object, tool, or process such that an optimal design can be achieved.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Plan and conduct an investigation to provide evidence that the change in an object's motion depends on the sum of the forces on the object and the mass of the object.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Analyze data to support the claim that Newton's Second Law of Motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Vermont - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret expressions that represent a quantity in terms of its context
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- LEGO MINDSTORMS Education NXT Software 2.1
- computer, loaded with NXT 2.1 software
- LEGO MINDSTORMS NXT brick (for example, part # 9841, for $148, available at http://shop.lego.com/en-US/NXT-Intelligent-Brick-9841?CMP=AFC-BP6648365778&HQS=9841)
- LEGO/HT- NXT Accelerometer/Tilt Sensor (MINDSTORMS), for $60, available at http://shop.lego.com/en-US/Accelerometer-Sensor-for-MINDSTORMS-NXT-285272
- laptop for data logging (must be able to run Microsoft Excel®)
- Accelerometer Survey, one per student
- Accelerometer Worksheet, one per student
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_accelerometer_activity1] to print or download.Pre-Req Knowledge
Physics, math concepts and technology (basic programming skills).
Introduction/Motivation
Imagine going around a sharp turn in a car; you lean against your car door (or another person) and feel as if you are about to be "pulled" off a merry-go-round. What you are feeling is centripetal force. Understanding centripetal forces is important for engineers who design devices that follow curved paths, such as airplanes, satellites, space ships, cars and even amusement park rides.
Today, you will act as engineers learning about the key factors that affect centripetal force and acceleration—mass, radius and velocity. All of these factors play an important role in how engineers design equipment that people count on to function correctly and safely every day, all over the world. For example, civil engineers need to understand centripetal acceleration to design highways that are safe for vehicles traveling at high speeds. Other engineers apply their understanding of centripetal acceleration to make sure that satellites follow the right path and can accurately give you directions via GPS.
An important aspect of engineering and robotics is how to acquire data and how to read graphs. At some point in your life, you will be asked to generate results from your experiments; however, you may not know exactly how to correctly read a graph and interpret the results. In today's activity you will be able to see your graphs while running the experiment at the same time. An advantage of this "dual view" is that by seeing the experiment and graphs simultaneously, you have an easier time interpreting the results.
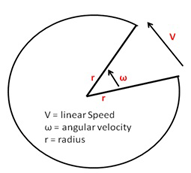
Force is the push or pull on an object, while centripetal force is the force that makes an object follow a curved path. Another way to think about centripetal force is to think about the net force that actually causes the acceleration in the direction of the net force. When that acceleration is center seeking, it is defined as centripetal acceleration. The magnitude of the centripetal acceleration can be associated with the velocity of the object and the length of the string on which the object is swinging.
We can define ω, as the angular velocity, which is simply how fast the radian measure of the angle changes as a function of time. This can be represented by the following equation (see Equation 1):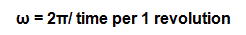
We can then convert the angular velocity to linear velocity via multiplying by the radius, which is represented in the following equation (see Equation 2):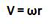
We can then use our liner velocity values to obtain centripetal acceleration by squaring the velocity and multiplying by the radius, as shown in this equation (see Equation 3) and in Figure 3.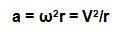
Procedure
Before the Activity
- Gather materials and make copies of the Accelerometer Survey and Accelerometer Worksheet.
- Ensure all computers available to the class are installed with LEGO MINDSTORMS NXT programming software and the MINDSTORMS NXT Data logging Program.
- Divide the class into teams of five students each. Remind students to work in their assigned groups the entire time.
With the Students
- Quick test to verify a working accelerometer: Direct students to plug the accelerometer into port 4 of the robot. Watch for a change in the view option of the NXT brick when they click the ultrasonic option. If they see a change in the view mode, then the accelerometer is working.
- Direct students to build their robot arms, making sure they are able to move back and forth in a curved path. (Note: It is important that teams build their robot arms correctly so that they can measure the amount of tilt in the robot across the three axes. Refer to Figures 4 and 5 for design schematics. Require students to demonstrate to you that they can move the arm back and forth; follow the path that the outside of the arm makes.)
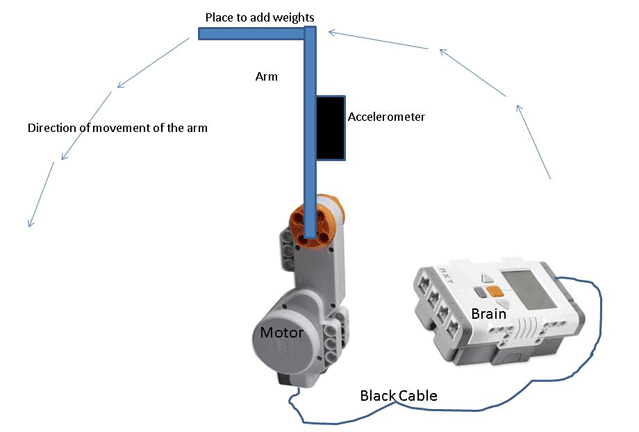
Figure 4. Robot arm design with accelerometer. - Open up the LEGO MINDSTORMS software and access the Data Logging Program.
- Have students program their robots to go back and forth in a curved path. Refer to Figure 5 for program guide.
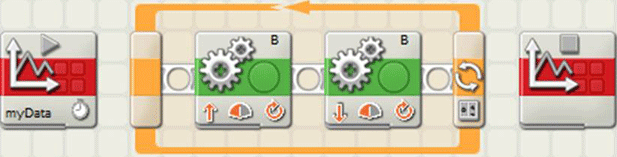
Figure 5. Screen capture of the program for data logging with accelerometer. - Have students attach their accelerometers to the robot arms, and plug in the accelerometer into port 4 of the robot.
- Direct students to position their accelerometer along different locations of their robot arms and monitor the tilt across the three different axes in the data logging program.
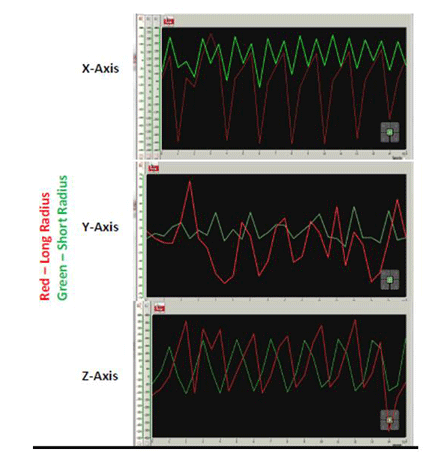
Figure 6. Accelerometer results from data logging show tilt across three axes. - Direct students to plot their results. What is the equation that relates to the results they obtained? (Note: Expect them to come up with Equations 1-3, presented in the Introduction/Motivation section.)
- Once the class has all the equations, ask them to connect their results to the equations.
- Direct students to change the mass on the arms and monitor the accelerometer across the three axes with the data logging. Also ask them to change the length of the arms and monitor the three axes with data logging. Have them export their results and plot the results in Excel.
- Ask students to connect their results to mathematical equations. Have them change the radius or weight on the arms and then use the equations to predict what will happen to velocity or centripetal acceleration.
Vocabulary/Definitions
accelerometer: Measures the change in G-force across the three different axes in the range of -2g to +2g, with a scaling of 200 counts per g. The accelerometer measures in g (1g = 200 counts). The counts can be thought of as the amount of tilt that the accelerometer acquires.
angular velocity: The magnitude of the rotational speed; usually measured in radians/ second.
centripetal acceleration: The acceleration that is directed towards the center of the circle.
centripetal force : A force that makes an object follow a curved path.
data logging: Records data over time via external sensors.
force: The push or pull on an object, which may change the shape of the object.
G-force: Acceleration that an object receives from gravity. It is an object's acceleration relative to free-fall. G-force can be measured as weight per unit mass.
Assessment
Pre-Activity Assessment
Quick Pre/Post Survey: At the beginning of the activity, administer to students the five-question Accelerometer Survey as a way to gauge their recall of the fundamentals of force, movement, centripetal force and accelerometers. Administer the same survey at activity end, to see the impact of the activity on their comprehension of the subject matter.
Guessing Game: Ask students to predict what features are important for high acceleration.
Activity Embedded Assessment
Design a Robot: Instruct students to make a connection between the robotic feature and the equations. Ask them to relate the robotic movements to linear and angular velocity.
Tuning the Equation: Ask students how the centripetal force would change when the radius of the arm changes or when the weight on the arm changes? Have them change the robot and make their own observations.
Post-Activity Assessment
Worksheet: At activity end, have students complete the Accelerometer Worksheet questions and math problems. Review their answers to gauge their depth of comprehension.
Investigating Questions
- How does the accelerometer measure the change in g across the three axes?
- How does the design of the robotic arm affect the centripetal acceleration?
- What features in the robotic arm are important for a high acceleration?
Troubleshooting Tips
Make sure that the arm moves back and forth and makes a hemisphere. Students are looking at the x and y axis for motion. Refer to Figure 4 to gain an understanding of the path that the arm makes when it moves back and forth.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Students learn the concept of angular momentum and its correlation to mass, velocity and radius. In an associated literacy activity, students use basic methods of comparative mythology to consider why spinning and weaving are common motifs in creation myths and folktales.

Students design, build and evaluate a spring-powered mouse trap racer. For evaluation, teams equip their racers with an intelligent brick from a LEGO© MINDSTORMS© EV3 Education Core Set and a HiTechnic© acceleration sensor.
Copyright
© 2013 by Regents of the University of Colorado; original © 2009 Polytechnic Institute of New York UniversityContributors
Jennifer S. Haghpanah; Carlo YuviencoSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 19, 2018








User Comments & Tips