Lesson Ring around the Rosie

Learning Objectives

After this lesson, students should be able to:

• Relate engineers' use of the concept of angular momentum to designing objects intended to spin as part of their mechanical workings, such as car and bicycle axles, compact disk players, fishing pole casting gear, textile and other industry machinery.
• Describe how mass and radius relate to angular momentum.
• Explain the law of conservation of angular momentum.
• Know where the axes are located on their bodies and what type of rotation is correlated to the different axes.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Pre-Req Knowledge

Forces (lift, weight, thrust, drag), linear momentum, Newton's first law of motion (inertia), center of mass and balance.

Introduction/Motivation

Understanding rotation is not only practical, it's FUN! Spinning around in a circle pulling our arms in and out till we get so dizzy we cannot even see straight is a favorite childhood (and adulthood) activity. Have you ever seen an ice skater or ballerina spin? Ferris wheels and merry-go-rounds also spin around, but on a much larger scale. Engineers take advantage of their understanding of rotational inertia and angular momentum to maximize the spin of these activities for people's thrill and enjoyment. Gymnasts, ballerinas and ice skaters apply mechanical physics and rotation to perform daring and crowd-pleasing rotations and spins. In this lesson, we discover how these acrobats maximize their spinning and how we can use our body to change our own rotational inertia and rotational velocity.

Following the lesson, students can expand their new learning to explore common motifs in creation myths and folktales with the associated activity Spin Me a Story.

Lesson Background and Concepts for Teachers

In regards to the vocabulary for this lesson, students will intuitively understand most of the terms, and the vocabulary will help them more thoroughly grasp the concept of rotation. Students can also conduct the fun and hands-on associated activity Super Spinners! to incorporate these vocab words in an exploratory experiment. 

Circular Motion

Circular motion is a term engineers use to describe revolutions and rotations. The difference between revolutions and rotations is whether the axis the object rotates about goes through the object (rotation) or does not (revolution). For example, a Ferris wheel rotates about its own axis (the center), but the people on the Ferris wheel revolve around the axis of the Ferris wheel (the axis is external to the rider's own axis). Similarly, the Earth rotates on its own axis, marked by days and nights, but the Earth also revolves around the Sun, marking the passage of years.

One way scientists and engineers describe circular motion is by measuring rotational speed. Rotational speed is the number of rotations or revolutions an object makes within a certain amount of time, which is often expressed in rotations or revolutions per minute (RPM).

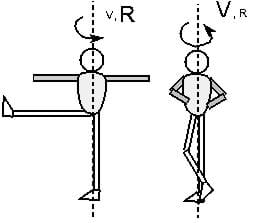
Rotational inertia depends upon how much mass an object has, and also the distribution of the mass. In other words, an object that is skinny (like an ice skater with her arms pulled in tight) has a different amount of rotational inertia than an object that is spread out (like an ice skater with her arms spread out wide). There are numerous equations that describe the rotational inertia of objects that depend on the distribution of mass. For this introductory lesson, we focus on the equation that describes rotational inertia if all the mass is located at one distance (for example a pendulum). This equation is:

I = mr²

Where: I = rotational inertia

m = mass

r = radius to concentrated mass

This equation shows the relationship of radius to the rotational inertia — the radius is squared! Therefore, rotational inertia — the tendency of a rotating object to keep rotating — is much less when the mass is located closer to the axis of rotation, because the radius is smaller. For example, a rotating object that is shaped like a big donut will tend to keep spinning longer than an object shaped like a pencil spinning on its tip.

Angular Momentum

Building on the concept of rotational inertia, engineers and scientists are also interested in what is called angular momentum. Angular momentum is a measurement of how difficult it is to make an object change the way it spins — to start spinning, stop spinning, speed up, slow down or change direction. It is related to rotational inertia — things with high rotational inertia will generally also have high angular momentum — but it also depends upon how fast an object is spinning. More specifically, angular momentum is defined as the rotational inertia times the rotational velocity. For simplification in the classroom, use the equation:

H = mvr²

Where: H = angular momentum

m = mass

v = rotational velocity

r = radius

This equation is true for objects with a large radius with respect to the object.

Angular momentum is a lot like linear momentum. Recall that linear momentum is a measurement of how much mass an object has and how fast it is moving in a straight line. Remember, too, that linear momentum can be transferred between objects through collisions, and that the linear momentum of a system before a collision is the same as the linear momentum of a system after a collision. This is called the law of conservation of linear momentum. Since angular momentum is like linear momentum, it should not be a surprise that there is a law of conservation of angular momentum, too.

The law of conservation of angular momentum says that if there is not something working to slow down a rotating object, the angular momentum of the system will not change. This law, expressed in the equation above, explains why ice skaters pull their arms in to spin faster! Imagine applying the equation to an ice skater. As an ice skater pulls her arms in to her body, her mass (m) does not change. And, as described by the law of conservation of angular momentum, her angular momentum (H) does not change. However, the radius (r) from her axis of rotation to her arms becomes smaller. The only way that angular momentum (H) cannot get smaller if the radius (r) gets smaller is if the skater's rotational velocity (v) gets bigger. In other words, when the skater's arms are next to her body, v is BIG, but r is SMALL. When the skater moves her arms outward, v is SMALL, but r is BIG! So, the v and r terms counteract each other, to conserve angular momentum.

Associated Activities

• Super Spinners! - In this hands-on activity, students experiment with rotational inertia, angular momentum and rotation speed by making variations of spinners and comparing the different spins they produce.

  Watch this activity on YouTube

• Spin Me a Story - Students use basic methods of comparative mythology to consider why spinning and weaving are common motifs in creation myths and folktales.

Lesson Closure

Ask students why they think rotational motion is important to engineers. For what other professions is an understanding of rotational movement important? Have the students sit on a rotating chair or stool and spin in a circle while slowly opening and closing their arms. Ask them to explain why they speed up and slow down in terms of rotation al inertia and rotational velocity. Try having the students jump while spinning, with their arms out and their arms in. Which is easier? Have them explain why.

Vocabulary/Definitions

Angular momentum: A measurement of how difficult it is to make an object change the way it spins.

Axis of rotation: The straight line about which rotation takes place.

Law of conservation of angular momentum: This law states that an object or system of objects will maintain a constant angular momentum unless acted upon by an unbalanced external torque.

Mass: A measure of how much matter there is in an object.

Revolution: The spinning motion that takes place when an object moves around an axis that does not go through the object (like the Earth around the Sun).

Rotation: The spinning motion that takes place when an object moves around an axis that goes through the object (like the Earth spinning, resulting in days and nights).

Rotational inertia: The tendency of an object that is spinning to continue circular motion.

Rotational speed: The number of rotations or revolutions per unit of time.

Velocity: Speed together with the direction of motion.

Assessment

Pre-Lesson Assessment

Discussion Question: Solicit, integrate and summarize student responses.

• Have you ever watched an ice skater spinning around? What do they do with their arms and legs? (Answer: They pull them in tightly to their body or over their head.) What happens when they move their bodies that way? (Answer: They spin faster.) Explain that the ice skater spins faster because of something called angular momentum, one important concept in understanding how things rotate. Tell them they will learn more about rotation during this lesson.

Post-Introduction Assessment

Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes and write the totals on the board. Give the right answer.

• True or False: Engineers use their understanding of rotational inertia and angular momentum to design roller coasters for the enjoyment of people. (Answer: True)
• True or False: Gymnasts and ice skaters use rotational inertia during their routines. (Answer: True. They use rotational inertia to perform daring and crowd-pleasing rotations and spins.)
• True or False: We can apply the concepts of rotational inertia to our own bodies on the playground. (Answer: True. We can demonstrate rotational inertia by spinning around.)

Lesson Summary Assessment

Inside-Outside Circle: Have the students form into two concentric circles (an inner-outer circle), so that each student has a partner facing him/her from the other circle. Ask the students to define a vocabulary word introduced in this lesson. Have partners consult each other to discuss the answer. Call on either the inner or outer circle group to answer the question all together. Repeat until all the vocabulary words have been addressed and answered correctly.

Using the Equations: Ask students to solve the following problems using the equations from the Lesson Background.

• A 60 kg skater has a radius to concentrated mass of 0.110 m radius when skating. Calculate her moment of inertia. (Answer: I = mr² = (60 kg)*(0.110 m) = 6.6 kg m²).
• Given:

H = 10 kg *m²/s

m = 70 kg

r = 5 m

Find v.

(Answer: H = mvr² --> v = H/(mr²) = (10 kg *m²/s)/(70 kg * (5m)²))= 0.00571 rad/s)

Lesson Extension Activities

Have the students make observations throughout the day, compiling a list all the objects they see that spin. Is each object one that spins naturally or did an engineer design it? What was the most interesting item they found that spins and what causes it to spin? Can they make it spin faster or slower, and how?

References

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.