Quick Look
Grade Level: 9 (8-10)
Time Required: 2 hours
(can be split into two 60-minute sessions)
Expendable Cost/Group: US $0.00 The activity requires non-expendable (reusable) materials including a computer and projector; see the Materials List for details.
Group Size: 3
Activity Dependency: None
Subject Areas: Algebra, Problem Solving
Summary
Students groups act as aerospace engineering teams competing to create linear equations to guide space shuttles safely through obstacles generated by a modeling game in level-based rounds. Each round provides a different configuration of the obstacle, which consists of two "gates." The obstacles are presented as asteroids or comets, and the linear equations as inputs into autopilot on board the shuttle. The winning group is the one that first generates the successful equations for all levels. The game is created via the programming software MATLAB, available as a free 30-day trial. The activity helps students make the connection between graphs and the real world. In this activity, they can see the path of a space shuttle modeled by a linear equation, as if they were looking from above.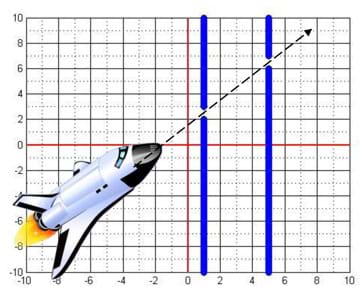
Engineering Connection
Before designing devices and structures, engineers model events, such as projectile motion, bouncing balls and rocket flights, to help them understand the motion that objects take. For example, aerospace engineers design spacecraft and develop vector equations to control the space shuttle. On Earth, we are able to stop movement instantly, but in space, without a medium such as air, roads or wind, space shuttles must rely on propulsion, which uses a reaction force to move an object. Space shuttles carry a limited supply of oxygen for the purpose of creating propulsion forces for movement. Making mistakes in the vector equation calculations can result in the depletion of precious materials that are essential to get back home. Thus, advance modeling of predicted space shuttle paths on x-y graphs is critical to plan and verify the distance, travel time and fuel required to complete the trip. NASA engineers were able to send a human to the moon and back with nothing but slide rulers—and without modern electronics—thanks to their very accurate vector calculations. As science progresses and technology becomes pervasive and costly to prototype, modeling can provide confidence to the expected real-world results.
Learning Objectives
After this activity, students should be able to:
- Develop a linear equation and determine its location and slope on a graph.
- Describe the benefits of modeling in engineering.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Create a computational model or simulation of a phenomenon, designed device, process, or system.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Analyze data using tools, technologies, and/or models (e.g., computational, mathematical) in order to make valid and reliable scientific claims or determine an optimal design solution.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Models (e.g., physical, mathematical, computer models) can be used to simulate systems and interactions—including energy, matter, and information flows—within and between systems at different scales.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
Common Core State Standards - Math
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Look for and make use of structure.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept.
(Grade
8)
More Details
Do you agree with this alignment?
-
Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear and quadratic functions, and simple rational and exponential functions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Model with mathematics.
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
Look for and make use of structure.
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept.
(Grade
8)
More Details
Do you agree with this alignment?
-
Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear and quadratic functions, and simple rational and exponential functions.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- paper and pencils
- Pre-Activity Quiz, one per student
- Game List Handout
- Game 1 Example Handout, one per student
- Post-Activity Quiz, one per student
For the teacher's use:
- computer and a projector with the extended display feature (enabling the use of one monitor and one projector at the same time)
- MATLAB® software by MathWorks (a few days in advance, download and install a free 30-day trial version of MATLAB from http://www.mathworks.com/programs/nrd/matlab-trial-request.html; do not do this more than 30 days before the activity)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_linear_activity1] to print or download.Introduction/Motivation
Today, you are going to be playing the roles of aerospace engineers. Aerospace engineers design aircraft, spacecraft, satellites and rockets, and develop vector equations to precisely control these flight vehicles. A vector is a direction of movement with a magnitude.
On Earth, we take it for granted that we can stop our movement instantly, but in space things are quite different. In space, because no medium like air, roads or wind exists to provide external forces such as friction, space shuttles rely on propulsion to stop or change direction. Propulsion uses a reaction force of something in order to move an object.
Imagine being on a "perfect" floor surface, one with no friction, so that the only way you can move is to either throw something in one direction, which pushes you in the opposite direction, or blow out air to propel you in the opposite direction. Propulsion in space works similarly to blowing out air, but space shuttles must carry their own oxygen in order to do so. If engineers make a mistake in their vector calculations and travel in the wrong direction in space, an additional amount of oxygen (the same or more) is required in order to correct the error in movement. The cost of such a mistake could be a lost satellite or human lives on the shuttle.
So today we will be dealing with the results of the vector calculations, which usually correspond to a known type of graph. In our case, we will examine linear equations, which describe straight lines, and we will use them to safely guide a space shuttle through obstacles (gates) that will be on your graphing paper.
How can a space shuttle end up traveling a perfectly straight path if the forces acting on it are 90 degrees apart (perpendicular)? Imagine this scenario: You attach a string to a cart and pull it left and your friend pulls it forward. If you both pull at the same rate, the cart's path will be straight. If you start slowing down or speeding up, the cart will start changing paths or even move in a curved motion. Let's draw it out. (Show students Figure 1 or draw it on the classroom board.) See how the cart's path changes based on the magnitude of force applied by you and your friend.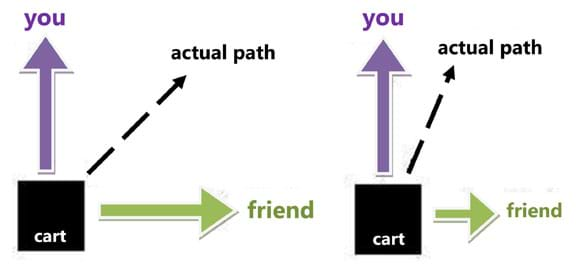
In today's exercise, we are analyzing the path of the "rocket" as a function of x. This means that the x-axis could represent the horizontal distance and y-axis represents the elevation or height of the rocket in the sky.
Procedure
Background
MATLAB software is designed for fast mathematical computation and the ability to handle script files, which are lists of instructions that execute in order. The programming language is local to MATLAB and it is not required or necessary to learn it for this activity.
The linear equations game is played by students choosing the slope value (m) and the intercept value (b) for linear equations in order for their "rockets" to fly through the gates that have been designed for them. Have students work in groups of three to come up with appropriate linear equations.
The zip file, Game Activity Folder, contains a folder with all of the required MATLAB code and functions. None of the files should ever be altered except PresetGoalsL.m (if you wish to make your own gates).
The PresetGoals.m file contains the coordinates for the gates in the following format:
LBound1X=1; this is the lower point X value of the first gate
LBound1Y=2; this is the lower point Y value of the first gate
HBound1X=1; this is the higher point X value of the first gate
HBound1Y=3; this is the higher point Y value of the first gate
LBound2X=5; this is the lower point X value of the second gate
LBound2Y=6; this is the lower point y value of the second gate
HBound2X=5; this is the higher point X value of the second gate
HBound2Y=7; this is the higher point y value of the second gate
Note: Spacing comes from the difference between y-values. (Example: LBound1Y=2 - HBound1Y=3 = 1, so this example has a gate spacing of 1.)
You can make your own games by editing games 13, 14 and 15, where each value is set to 0. Any changes made to the file must be saved in order for it to work when you run the main Game.m file. The first 12 games were designed with a gate spacing of 1 in order to encourage the use of decimals. 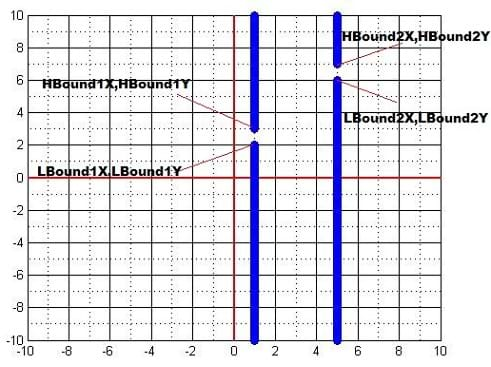
Note: It is important to mention to students that the gates work in a "greater than" or "less than" fashion, not in a "greater than or equal to" or a "less than or equal to" fashion. This means that the linear equation must fall above those starting points of each gate, and hitting the gate at its starting point is counted as hitting the obstacle.
Before the Activity
- A few days in advance of the activity, download and install a trial version of MATLAB.
- Obtain the zip file, Game Activity Folder, which contains a folder with all of the required MATLAB code and functions. Load and test the game.
- Set up the projector with extended display so that you are able to enter student values in the command window while the graphs show up on the projector.
- Make copies of the Pre-Activity Quiz, Game List Handout, Game 1 Example Handout, and Post-Activity Quiz.
With the Students
- Administer the pre-activity quiz, as described in the Assessment section.
- Present the Introduction/Motivation content to the class.
- Divide the class into groups of two or three student each.
- Explain how the game works: You are groups of aerospace engineers competing to create linear equations to guide space shuttles safely through obstacles of asteroids (or comets). In each scenario (game), you will be presented with a different configuration of the obstacle, which consists of two "gates" generated on an x-y graph. Your linear equations are inputs into autopilot on board the shuttle that determine the flight path through the two gates. The winning engineering team is the group that first creates all the required equations for each level (or if time runs out, the group that creates the most successful equations).
- As a class, go through the example handout, which explains how to solve Game 1.
- Launch the game by either pressing F5 or by pressing the "SAVE and RUN" button in the MATLAB top ribbon while the Game.m file is opened. (If launching does not occur, see the Troubleshooting Tips section.)
- The game asks you what game number you wish to play.
- Enter "1" (for the example, game 1), which generates a "Figure" file (containing the graph and gates for game 1) that appears in the bottom task bar of Windows.
- Slide this graph over to the projector's extended display, leaving the command window (which now asks for m and b values) on the computer/laptop screen.
- Enter a value (1) for m and a value (1.5) for b (results from the game 1 example handout). Hit enter and the line starts being drawn and passes through both gates. Then the program waits for an enter command after which it clears the graph and asks for a new game number.
- At this point, direct groups to start working on the rest of the nine problems found on the game list.
- Just as in the real world where engineers make calculations that must be correct or else consequences of loss or injury might occur, give groups only one chance per game to get it right. This means that each student should perform checks on the group's equation before presenting their answers to the teacher, who enters those values into the program.
- If the line does not pass through the gates, it hits the wall and stops being drawn. If this happens, the engineering team has failed its challenge. Then the program waits for enter to be pressed and asks for a game number. This allows for a fast transition between game numbers.
- Since the display is extended, the other competing groups do not see the m and b values entered, so they still have a chance to be successful on their own for any game number. The first engineering team to finish all the games on the games list wins.
- Conclude with a class discussion in which students share their experiences and lessons learned. Then make the real-world connection by asking: What benefits does modeling in engineering, such as what we did in today's activity/game, provide? (Short answer: Modeling enables engineers to foresee problems and avoid crashes and accidents, plan routes so as to conserve resources, test something before it is used in the real-world for the safety of people and property, and recreate failures and disasters to understand what happened. Prepare for the discussion by reading the Engineering Connection section, and the answer to question 2 of the post-activity quiz.)
- Administer the post-activity quiz, as described in the Assessment section.
Vocabulary/Definitions
gate: (In the context of this activity) An opening within the obstruction on the graph; one unit in predesigned games.
linear equation: An equation describing a line in the form y=mx+b, where m is the slope of the line and b is the y-intercept.
MATLAB: The mathematical software used in this activity. Described as a high-level language and interactive environment for numerical computation, visualization and programming. Made by MathWorks.
propulsion: A means of generating movement through a reactionary force.
vector: A magnitude with a direction, usually representing a force or a velocity.
Assessment
Pre-Activity Assessment
Pre-Quiz: Before starting the activity, have students complete the four-question Pre-Activity Quiz to assess their baseline ability to understand linear equations and the concept of propulsion.
Activity Embedded Assessment
Game Problems: During this multi-step activity, a total of 10 games (problems) are solved by each student group. Each game serves as an assessment of the group's collective ability to solve for a linear equation by determining two points on a line, and then finding the slope and y-intercept of the line. Even though groups may not be able to get a problem correct on the first try, after a team has solved an equation successfully, expect them to be able to continue this process until they finish all the games, since the steps are identical.
Post-Activity Assessment
Post-Quiz: At activity end, have students complete the two-question Post-Activity Quiz as a way to assess each student's ability to solve the same type of problem as they solved in the activity as a group. This helps to identify whether the game calculations work was done as a group or by just some individuals within the group. The assessment also asks students to describe the benefits of modeling in engineering.
Troubleshooting Tips
For the game to work, all files must in the same folder.
MATLAB might ask you if the files are in a different folder; simply clicking "add to path" after it pops up in the middle of the screen should solve that issue.
If something other than a number (such as a letter, symbol or blank space) is entered into m or b, the game will crash; simply restarting it fixes this.
Sometimes the command window does not appear after you install MATLAB; going to the View menu and enabling it solves this problem.
If a file with an extension ".m" is accidently renamed, it will most likely crash the game. (The only file that can be renamed is Game.m.) Simply downloading the activity folder again fixes the problem.
It is not possible to re-enter an m or b value. Simply cycling through the game with the incorrect m and b is the best way to come back to the game number you want.
To learn more about the computer/projector setup, search online for: extended display, extended desktop view, extended desktop view with projector, or variations of these search terms.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

The purpose of this lesson is to teach students how a spacecraft gets from the surface of the Earth to Mars. Students first investigate rockets and how they are able to get us into space. Finally, the nature of an orbit is discussed as well as how orbits enable us to get from planet to planet — spec...

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...
Copyright
© 2013 by Regents of the University of Colorado; original © 2012 Polytechnic Institute of New York UniversityContributors
Stanislav RoslyakovSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Additional support was provided by the Central Brooklyn STEM Initiative (CBSI), funded by six philanthropic organizations.
Last modified: June 18, 2021





User Comments & Tips