Quick Look
Grade Level: 10 (9-11)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 This activity requires the use of non-expendable (reusable) LEGO® MINDSTORMS® EV3 robot kits and software; see the Materials List for details.
Group Size: 6
Activity Dependency: None
Subject Areas: Measurement, Physics

Summary
Students use data acquisition equipment to learn about force and displacement in regard to simple and complex machines. In the engineering world, materials and systems are tested by applying forces and measuring the resulting displacements. The relationship between the force applied on a material, and its resulting displacement, is a distinct property of the material, which is measured in order to evaluate the material for correct use in structures and machines.Engineering Connection
One property that mechanical engineers study and measure is the spring or stiffness constant of a material. This involves the application of Newton's laws of motion and is known as Hooke's law. Various types of tests are conducted on different materials in order to determine the individual stiffness of each material. This is useful for engineers in determining the most suitable material for the design of a structure or machine to ensure safety and usability. The ability to analyze springs and elastic materials enables engineers to design complex structures.
Learning Objectives
After this activity, students should be able to:
- Explain and apply Hooke's law and its application to springs/elastic structures, F = kx.
- Explain the difference that a material makes in the design of a simple/complex machine.
- Measure properties and collect data from testing of materials.
- Describe how this application of Hooke's law is used to solve real-life engineering design problems.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Analyze data using computational models in order to make valid and reliable scientific claims.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Use a model to predict the relationships between systems or between components of a system.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Use mathematical representations of phenomena to describe explanations.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
-
Models (e.g., physical, mathematical, computer models) can be used to simulate systems and interactions—including energy, matter, and information flows—within and between systems at different scales.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
Common Core State Standards - Math
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Fit a linear function for a scatter plot that suggests a linear association.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Fit a linear function for a scatter plot that suggests a linear association.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- spring or inexpensive bungee cord with open hooks on each end
- LEGO MINDSTORMS EV3 robot, such as the EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3 (specifically the LEGO MINDSTORMS EV3 brick with ultrasonic sensor and LEGO parts will be used from the Core Set)
- LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first. At https://www.lego.com/en-us/mindstorms/downloads/download-software
- computer, loaded with EV3 1.2.1 software
- 1 piece of cardboard, ~6 x 6 inches, or stiff disposable plate, to use as a platform on the bottom end of the spring/bungee cord
- lab stand with attached clamp, or rod parallel to floor
- It's Spring Time Worksheet, one per student
Alternative: LEGO MINDSTORMS NXT Set:
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- computer loaded with the NXT 2.1 software
To share with the entire class:
- variety of weights that can be hung from the springs/bungee cords
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_springforce_activity1] to print or download.Pre-Req Knowledge
A basic understanding of force and simple/complex machines, as well as their use.
Introduction/Motivation
Everyday machines, such as cars and computers, are made of many different parts—each with their own purpose, so that they can move and function correctly. Many machines have parts that need to move back and forth so that the machine can perform a function over and over again. One of the parts used in a typical machine is a simple device called a spring. A spring is an elastic structure that, if working properly, comes back to its original position after it is pushed, pulled or bent. A typical spring is a coiled structure that resists pulling or pushing along its axis of coil, as shown in this diagram (draw Figure 1 on the classroom board).
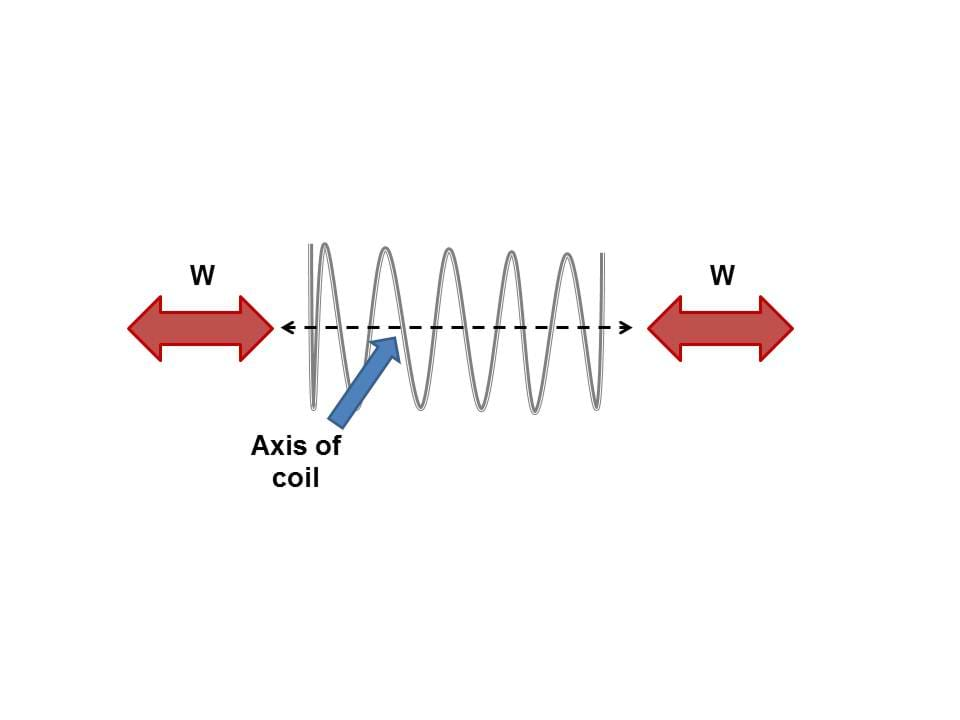
Many examples of springs are part of products that we use every day, such as rubber bands, bungee cords, the keys and buttons found on computers, elevators, appliances, toys (write these on the classroom board; ask students to think of additional examples).
As you might imagine from looking at this list, not all springs are used for one purpose or for the same type of job. Depending on the type and size of material used, the spring can be pushed to become a different size and/or shape. The part of the machine/device that the spring is attached to may need to move either a large or a small distance in order for the machine or device to function correctly. In order to predict how far a spring can compress or stretch, a relationship between the weight, or force applied (F), and the displacement of the spring (d) is given by Hooke's Law (see Equation 1):
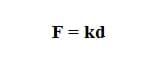
This equation is a linear equation, which means that it is in the form:
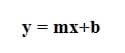
where m is the slope, and b is the y-intercept. In the case of Equation 1, there is no y-intercept, given that the spring begins in an unstretched state. As in a linear equation, the slope is the relationship between x (which is d in Equation 1) and y (which is F in Equation 1). The slope shows how y changes when x changes. This is similar to the relationship seen in Equation 1. When the displacement d changes, the force of the spring F changes. The relationship, or slope, of Equation 1 is called the stiffness constant. It is a property of each structure or material that does not change when it is being pushed or pulled, and it indicates its resistance to movement or change in shape. A rule of thumb: the higher the stiffness constant, the stiffer the material.
Analysis of springs and elastic materials in general are crucial for the design of complex structures. For example, for appropriate car suspension, the springs must be stiff enough so that the car body is sufficiently suspended above the ground. However, the springs should not be so stiff that the car deflects to variations of height on the ground (speed bumps, pot holes, etc.). Hence, springs or elastic structures must be designed and measured by engineers to handle the various motions of the car for maximum control and stability. So, in order to measure the stiffness of a structure or material, scientists and engineers run various types of tests using different equipment to measure the change in length or shape of a structure or material under different loads. The equipment often uses sensors, which are electronic devices that measure the change in length or shape of a material as it is being pushed or pulled. Also, sensors that can measure the amount of load placed on the piece of material itself are also used.
In this activity, it is important to emphasize the student's role as the "engineering experimenter," as well as thoroughly explain to students what and why they are experimenting with springs and weights. This experimentation is what scientists and engineers do every time a material is tested so that they can obtain data about the material being tested. In this case, we are testing the stiffness of a material (the bungee cord/spring) that is to be hung using the lab stand and clamp. Just as scientists and engineers do in their labs, we are running trial after trial of experimentation, taking measurements of the deflection, and causal weight, of the bungee cord, and calculating the stiffness constant using the data. We will also apply math and science-based concepts (such as calculating the slope) to graph the data. With the value of the stiffness constant, engineers can get a better idea of how a spring/bungee cord, or any stretchy material tested, reacts under weight. This is the main idea behind materials testing, in which a material's reaction is measured in order to better understand how it works and where it can be used appropriately.
Procedure
Before the Activity
- Gather supplies (see Figure 2) and make copies of the It's Spring Time Worksheet, one per student.
- Set up four stations with lab stands clamped to tables.
- Attach a spring or a bungee cord to each lab stand. (Note: Bungee cords may give data that is non-linear, especially when stretched to a large extent with large increments of weight. This is simply due to the fact that bungee cords or other similar spring-like contraptions are usually non-linear, where the force is not proportional to the distance stretched. However, if tested in small weight increments, linearity of plotted data may be observed.)
- Prepare the cardboard platform or attach a stiff paper plate near the bottom end of each spring/bungee cord by cutting a hole in the middle of the cardboard/plate.
- Attach a LEGO EV3 brick with ultrasonic sensor onto the bottom of each lab stand using LEGO building bricks, in order to measure the displacement. Many configurations of LEGO beams and blocks can work for the sensor to read the distance.
- The sensor actively reads the distance between the sensor base and the cardboard platform. To set it up using the EV3 from the LEGO MINDSTORMS kit, refer to the attached Measurement Instructions.

Figure 2. Each component of the spring mass sensor setup.
With the Students
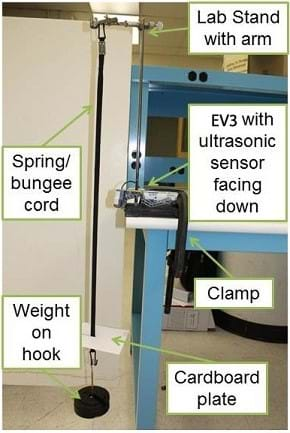
- Instruct students to set up their lab stations (see Figure 3). If not already attached, direct groups to place the cardboard platform/plate at the bottom end of the spring/bungee cord. (Note: If the platform is heavy enough to induce significant deflection, remind students to take the weight of the platform into account in their analyses.)
- Direct students to record the initial position of the cardboard platform/plate.
- Very carefully, have students place an increment of weight (starting with lightly) on their platform. Record the position of the cardboard plate each time the weight is incremented. Alternate weights, using at least four different weights.
- On their worksheets, have students calculate the displacement (d) after each weight increment. Make sure to convert units appropriately, such as position measurements from centimeters to meters.
- After filling in the table, direct students to plot a force (on y-axis) vs. displacement (on x-axis) graph by hand on their worksheets. Have students draw best-fit lines through all the data points. Using the endpoints of the best-fit line, have them calculate the slope using the slope equation (Equation 3), where the y-terms are the difference in load values, and the x-terms are the difference in deflection values. The slope of the graph is the stiffness constant, k. As stated before, the higher the k value, the higher the stiffness of the bungee cord or spring tested (see Equation 3).
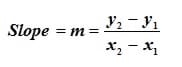
Equation 3. The equation to calculate scope.
Vocabulary/Definitions
sensor: Device that measures or "senses" a specific quantity (temperature, distance, level of light/darkness, among other things).
spring: Elastic device that returns to its original shape when it is pressed, bent, pushed or pulled.
stiffness: Resistance to change of shape of a material or structure.
Assessment
Pre-Activity Assessment
What are springs? Gauge students' understanding of the concepts of springs. Hold up a spring or a bungee cord in front of the class and ask students to tell you what they know about each. Students should raise their hands and speak one answer at a time. No two students can answer the same. On the chalk/white board, create a list of words for students to refer back to during the activity.
Activity Embedded Assessment
Worksheet Data Collection & Analysis: While students are completing the It's Spring Time Worksheet, roam the classroom to make sure they understand the data collection table and graph. Evaluate students on two criteria: conducting experimental measurements and interpretation of the resulting data, with respect to applied theory.
When conducting experimental measurements, expect the groups should have similar displacement results, given that the same-size spring or bungee cord is used by each group.
When interpreting data, students should be able to obtain information about test trials from a graph plotted with their own data. From simply looking at a graph and comparing it to other similar graphs, students should be able to briefly characterize the material. Ask the following questions:
- Is what we tested a stiff material? (Answer: Stiff materials generally demonstrate substantially low deflection.)
- Does adding more material to a bungee cord make it stiffer? (Answer: Not necessarily. Generally, established, straightforward correlations exist for many materials, in which higher densities signify higher modulus. Therefore, adding more material may add more support to the system, but will not increase the density or stiffness.)
Design within Constraints: Through conversations with student groups, gauge their understanding of design constraints, an important component of engineering. Ask the following:
- Do all of the springs or bungee cords fit this requirement or constraint? (Answer: Not necessarily. This would have to be determined with the data points obtained from the sensor measurements.)
To explain, take a maximum value of weight from one of the data points or graphs that one of the groups measured. Then assume that a spring/bungee cord is used to hold the weight without deflecting an arbitrary set distance (say 20 cm). If any data points have a deflection value of more than 20 cm, for example, then the bungee cord or spring would not be able to fit such criteria.
Post-Activity Assessment
Is Everything a Spring?! Discuss with the students about materials other than springs/bungee cords may be tested, and if they are tested in a similar fashion to what was done for this activity. Students should be able to have a better idea of the concept of stiffness in materials and determine the everyday materials that can be considered relatively stiff as compared to other materials (for example, concrete or plastic).
Safety Issues
Slowly load and unload the weights from the cardboard platform/plate to ensure the spring or bungee cord does not flail.
Troubleshooting Tips
If measurements are difficult to read, have students steady the hanging weight to ensure the most accurate reading possible.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students calculate stress, strain and modulus of elasticity, and learn about the typical engineering stress-strain diagram (graph) of an elastic material.

Students are introduced to the concept of viscoelasticity and some of the material behaviors of viscoelastic materials, including strain rate dependence, stress relaxation, creep, hysteresis and preconditioning. Viscoelastic material behavior is compared to elastic solids and viscous fluids.

Students are introduced to Hooke's law as well as stress-strain relationships. Through the lesson's two-part associated activity, students 1) explore Hooke's law by experimentally determining an unknown spring constant, and then 2) apply what they've learned to create a strain graph depicting a tumo...

Students investigate potential energy held within springs (elastic potential energy) as part of the Research and Revise step. The lesson includes a dry lab that involves pogo sticks to solidify the concepts of spring potential energy, kinetic energy and gravitational energy, as well as conservation ...
Copyright
© 2013 by Regents of the University of Colorado; original © 2012 Polytechnic Institute of New York UniversityContributors
Ronald Poveda; Irina IgelSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020






User Comments & Tips