
Summary
Students learn the relevant equations for refraction (index of refraction, Snell's law) and how to use them to predict the behavior of light waves in specified scenarios. After a brief review of the concept of refraction (as learned in the previous lesson), the equations along with their units and variable definitions, are introduced. Student groups work through a few example conceptual and mathematical problems and receive feedback on their work. Then students conduct the associated activity during which they practice using the equations in a problem set, examine data from a porous film like those used in biosensors, and apply the equations they learned to a hypothetical scenario involving biosensors.Engineering Connection
In engineering, it is not enough to merely understand the concepts or ideas behind physical phenomenon such as refraction. If engineers want to take a physical law of the universe and turn it into a product that performs a task, then the phenomenon must be quantifiable—they must be able to assign a mathematical function or equation to it that accurately predicts an outcome if the input parameters are manipulated purposefully. In a way, engineers are dictating the setup and letting nature take its course to a conclusion that the engineers can foresee from the start. Similarly, students play the role of engineers in this lesson when they use an equation for refraction (Snell's law) to predict what light will do given a specific scenario. They further act as engineers when they use this equation to define what a biosensor can be made to do under given conditions.
Learning Objectives
After this lesson, students should be able to:
- Solve Snell's law problems for a single variable.
- Accurately draw the path a light ray will take when given the index of refraction of the substance(s) through which it travels.
- Accurately describe how the path of a light ray changes when the index of refraction of the substance(s) and/or the incident angle are changed.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-1. Analyze a major global challenge to specify qualitative and quantitative criteria and constraints for solutions that account for societal needs and wants. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Analyze complex real-world problems by specifying criteria and constraints for successful solutions. Alignment agreement: | Criteria and constraints also include satisfying any requirements set by society, such as taking issues of risk mitigation into account, and they should be quantified to the extent possible and stated in such a way that one can tell if a given design meets them. Alignment agreement: Humanity faces major global challenges today, such as the need for supplies of clean water and food or for energy sources that minimize pollution, which can be addressed through engineering. These global challenges also may have manifestations in local communities.Alignment agreement: | New technologies can have deep impacts on society and the environment, including some that were not anticipated. Analysis of costs and benefits is a critical aspect of decisions about technology. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS4-1. Use mathematical representations to support a claim regarding relationships among the frequency, wavelength, and speed of waves traveling in various media. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use mathematical representations of phenomena or design solutions to describe and/or support claims and/or explanations. Alignment agreement: | The wavelength and frequency of a wave are related to one another by the speed of travel of the wave, which depends on the type of wave and the medium through which it is passing. Alignment agreement: | Empirical evidence is required to differentiate between cause and correlation and make claims about specific causes and effects. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS4-2. Develop and use a model to describe that waves are reflected, absorbed, or transmitted through various materials. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop and use a model to describe phenomena. Alignment agreement: | A sound wave needs a medium through which it is transmitted. Alignment agreement: When light shines on an object, it is reflected, absorbed, or transmitted through the object, depending on the object's material and the frequency (color) of the light.Alignment agreement: The path that light travels can be traced as straight lines, except at surfaces between different transparent materials (e.g., air and water, air and glass) where the light path bends.Alignment agreement: A wave model of light is useful for explaining brightness, color, and the frequency-dependent bending of light at a surface between media.Alignment agreement: However, because light can travel through space, it cannot be a matter wave, like sound or water waves.Alignment agreement: | Structures can be designed to serve particular functions by taking into account properties of different materials, and how materials can be shaped and used. Alignment agreement: |
International Technology and Engineering Educators Association - Technology
-
Optimize a design by addressing desired qualities within criteria and constraints.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Tennessee - Science
-
Investigate reflection, refraction, diffraction, and interference of light waves.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Examine properties of light waves.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve problems related to Snell's law [Index of refraction: n = (sin θr / sin θi); Snell's law: ni sin θi = nr sin θr].
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Pre-Req Knowledge
Students must have:
- A basic knowledge of algebra and elementary trigonometry, and be able to solve simple algebraic and trigonometric problems.
- A conceptual understanding of refraction and the challenge problem, as presented in the first lesson Tell Me Doc – Will I Get Cancer?
Introduction/Motivation
In the last two lessons, we learned about the refraction of light, what it is, how it works, and its potential for creating biosensors that could detect cancer-causing genes. After all, our ultimate goal is to solve our challenge question (as necessary, ask students to recall/explain the challenge question).
But we still have an incomplete picture. We know the basic ideas, but suppose I made a biosensor out of a porous film, as we discussed. I may see different colors at different angles, like we saw in our previous activity Bubbles and Biosensors, but how does that tell me whether or not my sample has a cancer-causing gene in the pores?
We need some more definite answers—and as you have probably gathered from your experiences in this class, that suggests an equation, a way we can take given information, and predict precisely what will happen. Doing this moves us one step closer to solving our challenge question—how we can use a nanoscale biosensor to detect a cancer-causing gene, and find out someone's genetic risk of cancer.
To do so, we will first learn the equations, including what each variable means, and the math tricks necessary to solve them. Then we will get to look at some more porous thin films used in biosensors, but instead of just looking at them this time, we'll get to see the data that scientists collect from them, and use our new equations to prove how the presence of a certain gene can change this data, and thus inform doctors of what they need to know about their patients.
For the purposes of the Legacy Cycle, we have now reached the Test Your Mettle phase. That means that now you get to see how well you really understand this stuff by solving problems—and if you mess up, that's okay, you can always go back and fix it, to make sure you have it all right before we make our poster to complete the project.
Lesson Background and Concepts for Teachers
Legacy Cycle Information
This third lesson of the unit constitutes the Test Your Mettle phase of the Legacy Cycle, and is designed to give students an opportunity to do something with the concepts they have learned, and get feedback on whether or not they have mastered the concepts and if their emerging solution to the challenge problem is correct. The intent of the assessment tools is to measure students' mastery and inform them of their progress so that they can try again and modify as needed.
Lecture Information
Refraction, or the bending of light, is caused by the fact that light moves at different speeds in different materials. The ratio of the speed of light in a material to its speed in a vacuum is referred to as the "index of refraction," or "n." The mathematical form is n = c/v, where c is the speed of light in a vacuum, and v is the speed of light in that material.
In 1621, Willebrord Snellius derived an equation that related this index of refraction to the angle at which light is refracted. Suppose light travels from substance 1 into substance 2—Snell's law would look like this: n1sinθ1 = n2sinθ2 , where n is the index of refraction (for substances 1 and 2) and θ is the angle at which light is refracted, as measured from a line perpendicular to the surface of the material (again for substances 1 and 2). Figure 1 illustrates this equation.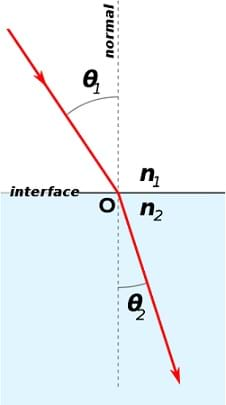
For students' purposes, they must be able to solve this equation for a missing variable, given the other variables in the form of a word problem, and predict what will happen to a variable on the other side of the equation when a given variable is changed.
Follow this sequence of steps to present the lesson and associated activity (When Silicon Talks: Refraction Equation Practice & Bio Lab Work) :
- After presenting the Introduction/Motivation content, briefly review the underlying concepts of refraction (see the first lesson in this unit for more detailed information). Do this by calling on students in an informal survey, or short questions that serve as a mini pre-quiz.
- Have students (in groups or individually) look up the index of refraction and Snell's law equations, either in textbooks or online (see a suggested website in the Additional Multimedia Support section), and write down the equations and what each variable stands for, as well as the units. (To save time, have students look up the equations as a "bell ringer" activity before presenting the Introduction/Motivation content.)
- After students have found the two equations, review the details of their findings to make sure they have the correct information. If time permits, do one or two quick example problems as a class so students can see how to assign numbers to the appropriate variables as well as the math steps. Example problems:
Example Problem 1: Light travels at a speed of 2.5 x 108 m/s in a certain substance. What is the index of refraction of this substance? Answer: n = c/v, so n = (3 x 108) / (2.5 x 108) = 1.2
Example Problem 2: Light traveling in a substance with index of refraction 1.2 is incident upon water at an angle of 34°. If the light is refracted at an angle of 30.3°, what is the index of refraction of water? Answer: n1sinθ1 = n2sinθ2 , so substituting our values gives us (1.2) sin(34) = n2(sin 30.3). Solving for n2 gives us n2 = ((1.2)(sin34))/(sin 30.3) = 1.33
- Conduct the associated activity. During the activity, be sure to emphasize how a change in refractive index (caused by the presence of a substance in the porous film, or the binding of a target molecule to the molecule in your film) causes a shift in wavelengths of light that get reflected, which is observable and measurable data output. The way this works is if we take a reflectance measurement using a spectrometer, we get a sinusoidal wave pattern when viewing percentage of light reflected vs. wavelength. This is what we would expect, since the pores cause specific wavelengths of light to interfere constructively (aka, an interference pattern). But if the index of refraction of the film changes, we expect to see different wavelengths interfering constructively (see detailed explanation in the lesson 2 of the unit). This means that the sinusoidal pattern on the graph would "shift" left or right to indicate that longer or shorter wavelengths are interfering constructively as they are refracted. Snell's law confirms this by indicating how a change in "n" creates a change in "θ" to produce different constructively interfered wavelengths.
- Conclude the activity by having students individually complete the final problem on the activity worksheet.
- Then conclude the lesson by assigning students to answer the two questions provided in the Assessment section.
Associated Activities
- When Silicon Talks: Refraction Equation Practice & Bio Lab Work - Students investigate how different wavelengths of light reflect differently from porous silicon surfaces when parameters are changed. After completing a set of practice problems using refraction equations, they move on to the lab portion of the activity, which may be conducted in two different ways—either using expensive equipment and limited availability porous silicon surfaces or using thin films students create from nail polish.
Vocabulary/Definitions
index of refraction: The ratio of the speed of light in a material to its speed in a vacuum. The mathematical form is n = c/v, where c is the speed of light in a vacuum, and v is the speed of light in that material.
refraction: The bending of light caused by a change in speed as it enters a different material.
Snell's law: A scientific equation that relates the index of refraction of a substance to the angle at which light bends in that substance. The mathematical form is n1sinθ1 = n2sinθ2 , where n is the index of refraction (for substances 1 and 2) and θ is the angle at which light is refracted, as measured from a line perpendicular to the surface of the material (again for substances 1 and 2).
Assessment
Pre-Lesson Assessment
Concept Review: Use a review of the previous lessons as an informal assessment of student retention of the concept of refraction. Do this with a show of hands in answer to short questions.
Post-Introduction Assessment
Since students are conducting the associated activity mid-lesson, refer to the assessment suggestions provided in the activity write-up.
Lesson Summary Assessment
Questions: Write the following questions on the board and have students answer them individually, to be turned in and graded as an assessment of their comprehension of the lesson/activity subject matter.
- Describe how this phenomenon known as Snell's law could help us solve our original challenge question. In other words, how could this help us detect the presence of cancer-causing genes? (Example answer: Since the substance itself determines the angle at which light bends, then perhaps we can know if a gene is present simply by measuring the angle to be a certain value, because this would indicate a change in the substance itself [caused by the presence of the gene we are seeking].)
- What other practical uses might arise from Snell's law? List at least two possibilities and explain your reasoning in at least three complete sentences. (Example applications: Fiber optics/sending a signal; military uses such as trajectories of water-based missiles or metamaterials for invisibility; lenses [glasses and contacts, telescopes, microscopes, cameras, binoculars, projectors] and/or materials analysis [determining properties of unknown or new composite materials].)
Additional Multimedia Support
A suggested website for students to look up the index of refraction and Snell's law equations as part of the assigned lesson research: http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html. At this website, click "Light and Vision," then "Refraction."
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Students learn about the science and math that explain light behavior, which engineers have exploited to create sunglasses. They examine tinted and polarized lenses, learn about light polarization, transmission, reflection, intensity, attenuation, and how different mediums reduce the intensities of ...

Through four lessons and three hands-on activities, students learn the concepts of refraction and interference in order to solve an engineering challenge. Students learn about some high-tech materials and delve into the properties of light, including the equations of refraction (index of refraction,...

After a demonstration of the deflection of an electron beam, students review their knowledge of the cross-product and the right-hand rule with example problems. Students apply these concepts to understand the magnetic force on a current carrying wire. Through the associated activity, students furthe...
References
Klein, Stacy S., Harris, Alene H. "A User's Guide to the Legacy Cycle." Journal of Education and Human Development. Vol. 1, No. 1, 2007. http://www.scientificjournals.org/journals2007/articles/1088.pdf
Nave, Carl R. "Refraction of Light." 2012. HyperPhysics, Department of Physics and Astronomy, Georgia State University, Atlanta, GA. Accessed June 26, 2013. (Source of Snell's law explanation, with some adaptation) http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
Refractions and Lenses: Problem Set. 1996-2014. Ray Optics: Refraction and Lenses, The Physics Classroom. Accessed June 26, 2013. (Source of worksheet problems, with some adaptation). http://www.physicsclassroom.com/calcpad/refrn/problems.cfm
Copyright
© 2014 by Regents of the University of Colorado; original © 2012 Vanderbilt UniversityContributors
Caleb SwartzSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: June 30, 2019










User Comments & Tips