
Summary
Students learn about the scientific and mathematical concepts around electromagnetic light properties that enable the engineering of sunglasses for eye protection. They compare and contrast tinted and polarized lenses as well as learn about light intensity and how different mediums reduce the intensities of various electromagnetic radiation wavelengths. Through a PowerPoint® presentation, students learn about light polarization, transmission, reflection, intensity, attenuation, and Malus’ law. A demo using two slinky springs helps to illustrate wave disturbances and different-direction polarizations. As a mini-activity, students manipulate slide-mounted polarizing filters to alter light intensity and see how polarization by transmission works. Students use the Malus’ law equation to calculate the transmitted light intensity and learn about Brewster’s angle. Two math problem student handouts are provided. Students also brainstorm ideas on how sunglasses could be designed and improved, which prepares them for the associated hands-on design/build activity.Engineering Connection
Engineers begin design challenges by learning about relevant science and math concepts in order to fully understand the problem. For instance, engineers are currently trying to broaden the telecommunications spectrum and increase bandwidth to accommodate the rise in data streaming applications. The plan is to add frequencies in the 28–64 GHz range, which are not yet used in data streaming because of some limitations in their wave characteristics. The millimeter wave, as waves with this frequency are called, is prone to large attenuation (reduction in power) as it travels through walls and even human bodies. It also has a very small cell coverage area, which increases the need for antennas and cellular stations. Similar to how engineers are investigating and testing to learn more about radio/microwaves to accomplish this task, through this lesson, students learn about light properties to help them design and refine new types of sunglasses in the associated activity.
Learning Objectives
After this lesson, students should be able to:
- Calculate the light intensity when two polarizing films are used.
- Compare and contrast tinted and polarized glass.
- Evaluate light attenuation through different mediums.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS4-3. Evaluate the claims, evidence, and reasoning behind the idea that electromagnetic radiation can be described either by a wave model or a particle model, and that for some situations one model is more useful than the other. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Evaluate the claims, evidence, and reasoning behind currently accepted explanations or solutions to determine the merits of arguments. Alignment agreement: A scientific theory is a substantiated explanation of some aspect of the natural world, based on a body of facts that have been repeatedly confirmed through observation and experiment and the science community validates each theory before it is accepted. If new evidence is discovered that the theory does not accommodate, the theory is generally modified in light of this new evidence.Alignment agreement: | [From the 3–5 grade band endpoints] Waves can add or cancel one another as they cross, depending on their relative phase (i.e., relative position of peaks and troughs of the waves), but they emerge unaffected by each other. (Boundary: The discussion at this grade level is qualitative only; it can be based on the fact that two different sounds can pass a location in different directions without getting mixed up.) Alignment agreement: Electromagnetic radiation (e.g., radio, microwaves, light) can be modeled as a wave of changing electric and magnetic fields or as particles called photons. The wave model is useful for explaining many features of electromagnetic radiation, and the particle model explains other features.Alignment agreement: | Models (e.g., physical, mathematical, computer models) can be used to simulate systems and interactions—including energy, matter, and information flows—within and between systems at different scales. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS4-4. Evaluate the validity and reliability of claims in published materials of the effects that different frequencies of electromagnetic radiation have when absorbed by matter. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Evaluate the validity and reliability of multiple claims that appear in scientific and technical texts or media reports, verifying the data when possible. Alignment agreement: | When light or longer wavelength electromagnetic radiation is absorbed in matter, it is generally converted into thermal energy (heat). Shorter wavelength electromagnetic radiation (ultraviolet, X-rays, gamma rays) can ionize atoms and cause damage to living cells. Alignment agreement: | Cause and effect relationships can be suggested and predicted for complex natural and human designed systems by examining what is known about smaller scale mechanisms within the system. Alignment agreement: |
Common Core State Standards - Math
-
(+) Use inverse functions to solve trigonometric equations that arise in modeling contexts; evaluate the solutions using technology, and interpret them in terms of the context.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Michigan - Math
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Use inverse functions to solve trigonometric equations that arise in modeling contexts; evaluate the solutions using technology, and interpret them in terms of the context.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Michigan - Science
-
Evaluate the claims, evidence, and reasoning behind the idea that electromagnetic radiation can be described either by a wave model or a particle model, and that for some situations one model is more useful than the other.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Evaluate the validity and reliability of claims in published materials of the effects that different frequencies of electromagnetic radiation have when absorbed by matter.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/mis-2231-light-properties-sunglasses-electromagnetic-waves-polarization] to print or download.Pre-Req Knowledge
- Familiarity with the electromagnetic spectrum, specifically its increasing frequencies for radio waves, microwaves, infrared, visible light, ultraviolet light, x-rays and gamma waves.
- Familiarity with the differences between opaque, transparent and translucent mediums.
- An understanding of the structure of electromagnetic waves, what creates them, and how they propagate.
Introduction/Motivation
(In advance:
- Make copies of the Quick Check Handout for students to use during the middle of the presentation, and the How Do Sunglasses Work? Homework, one each per student.
- For each group of 2-4 students, distribute one pair each of polarized and unpolarized sunglasses. Label the polarized sunglasses as “1” and the unpolarized sunglasses as “2.”
- Have available two long, coiled springs (such as Slinkys) for in-class demonstrations [see slide 6].
- For each group, have available two slide-mounted polaroid films for the mini-activity [see slide 8]. This is linear polarizing film for use with visible light. If you align two filters, light passes through. If you rotate one filter 90°, light is completely blocked.
- Have students bring out paper and pencils for notetaking.
Supplies note:
- Even though polarized sunglasses can be expensive, the brand is not important for this lesson and relatively inexpensive ones [$9 each] can be found on Amazon. Unpolarized [just tinted] sunglasses are less expensive [< $1 each] and are available at party stores or Amazon [$15 for 24].
- Suggest obtaining polaroid filters that are mounted in 35 mm slide frames, such as item #P2-9405, a pack of 50 slide-mounted polarizing filters for $35 from Arbor Scientific.
Have the 14-slide How Do Sunglasses Work? Presentation [a PowerPoint® file] ready to show the class. Organize the class into groups of 2-4 students and then address the class.)
In front of you, each group has two sunglasses that look about the same. In the next five minutes, closely examine both pairs. Record the similarities and differences between the sunglasses so we can talk about them later as a class. Do more than just look at them; put them on as part of your examination. (As students examine the sunglasses, circulate the classroom to make sure they are taking notes and engaged in discussion.)
Let’s discuss what you observed. Draw a two-circle Venn diagram in your notes. (On the classroom board, draw two large, halfway-overlapping circles—a basic Venn diagram.)
Let’s compare and contrast the two sunglasses. Group 1, tell us one similarity and one difference that your team observed when examining the two sunglasses. (Record all responses in the classroom board Venn diagram to organize three categories of observations: unique to sunglasses 1, unique to sunglasses 2 and common to both sunglasses. Have students record the same in their notes. Keep going around to all the groups to gather their observations; expect each group to contribute at least one similarity and one difference. If a group repeats an idea that is already on the board, ask them to share an original one. Expect the similarities to include: both have tinted lenses, are similar in general design and parts, and both reduce the light intensity when you look through them. The key difference is that the polarized sunglasses enable you to see a sharper image.)
As we can see, both pairs of sunglasses have tinted lens, the same general design, and reduce the amount of light going through. However, one pair of sunglasses enables us to see a sharper image. This is because of light polarization. In today’s lesson, we will learn the principles of light polarization, intensity and what happens when different electromagnetic radiation passes through different mediums so we can figure out how sunglasses are engineered.
(Begin the slide presentation. The slide notes provide teacher information and suggested questions to make it an interactive presentation, with similar/additional information provided below. The slides are animated, so a mouse, spacebar or down arrow click reveals the next item.)
(slides 1-2) What do sunglasses do? Have students brainstorm in their small groups about what they think is necessary to create an effective pair of sunglasses. Ask them: What are the key objectives of good sunglasses? Then have teams share their ideas with the class as you write them on the classroom board. Then begin organizing them into three categories: reducing glare, reducing light intensity and blocking UV light—the key characteristics of sunglasses.
(slide 3) Review the lesson objectives.
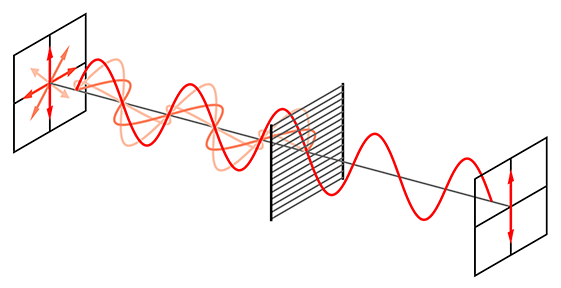
(slide 4) Review electromagnetic wave structure. Expect students to be aware of these concepts. A gif animation diagram is provided (same as Figure 1). Ask the two questions on the slide and listen to student answers before revealing the answers.
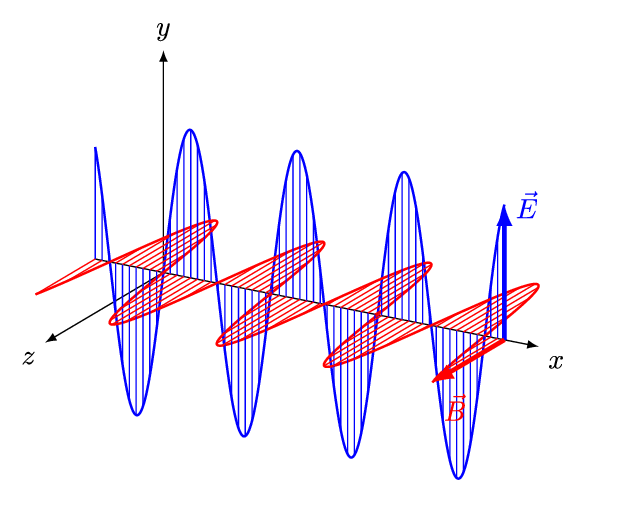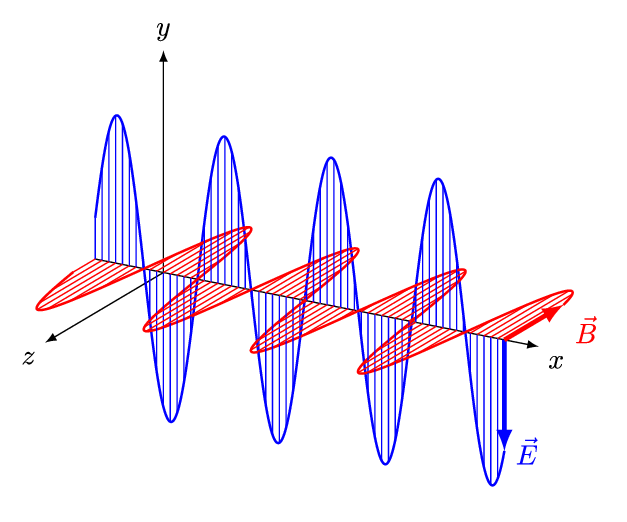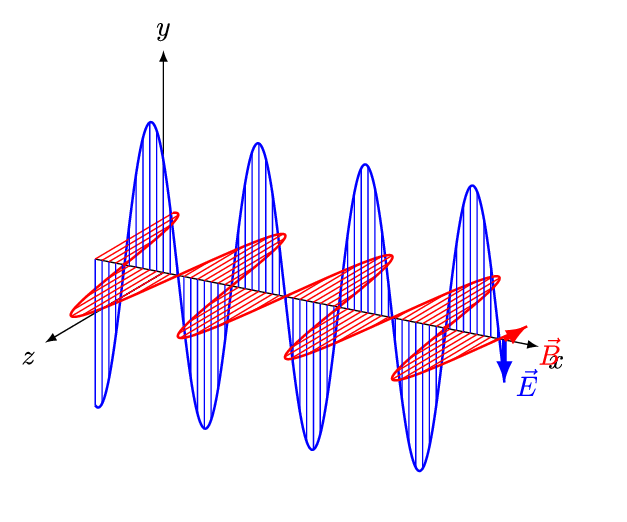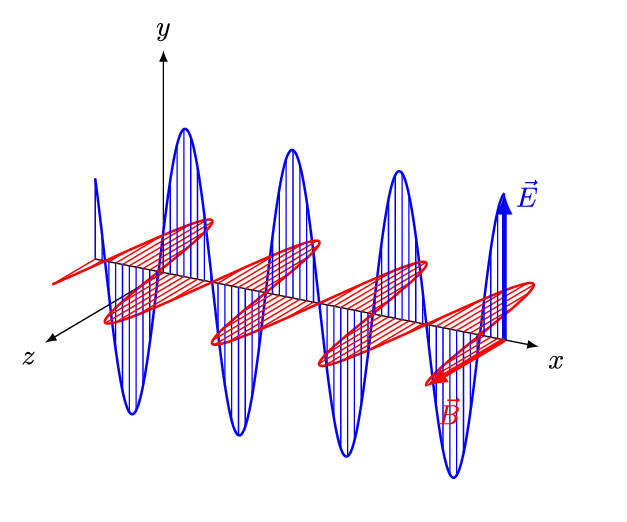
(slide 5) EM Wave Properties and Light Polarization: Ask students the two questions on the slide about the properties of electromagnetic waves and light polarization. Listen to their answers before revealing the answers. For example, expect them to know that light travels 3.0 x 108 meters per second, travels in straight lines and has more than one disturbance. Given that light (and all electromagnetic waves) has more than one disturbance, it also has more than one polarization; give students five minutes to discuss in their groups the meaning of polarization. Then have each team share its definition with the class before moving on.
(slide 6) Light Polarization: Inform students that polarization refers to the direction of the vibration. Draw a few transverse waves on the classroom board to help explain the concept. Even better, show students a few demonstrations, such as by using two long coiled springs to demonstrate the different-direction polarizations. For example, have four students come up to the front of classroom. Have one pair create a vertical disturbance using one spring and behind them the other pair creates a horizontal disturbance using the second spring. Ask students to explain how this “light” is polarized. Then ask students about the polarization of light and other electromagnetic waves. Then go through the four ways to polarize light: transmission, reflection, refraction and scattering. In this lesson, we focus on transmission and reflection.
(slide 7) Transmission “Filter” Method Polarization: The polarization of light can change by passing it through polaroids. What are polaroids? Listen to student answers before clicking to reveal the definition and a visual diagram (same as Figure 3) of polarization by transmission. Polaroids are special filters that are chemically designed to let through only a specific polarization of light. Have students try to explain the transmission polarization concept before going over the rest of the slide. Use the diagram to help students understand a little better: The light in the diagram is vertically polarized and was polarized through a vertical polaroid.
(slide 8) Polarization by Transmission Mini-Activity: Give each group two polaroid filters and have students perform the mini-activity as directed by the three questions on the slide. Have students record in their notes their observations and answers. After giving students time to answer each question, go over the answers as a class.
(slide 9) Reflection Method: Use this slide to explain how light becomes polarized through reflection, such as when light hits the hood of a car or the surface of a lake’s water. A supporting diagram (same as Figure 5) is provided to show polarization through reflection and refraction, and introduce the angle of incidence.
(slide 10) Reflection Method: Have students continue to take notes on the information provided on this slide. At the end of the slide, ask students to determine which direction sunglasses are polarized. Have them make a hypothesis based on the reflection method and then use the slide-mounted polaroids to test the hypothesis to determine which direction is polarized. After giving students 5-7 minutes to experiment, discuss their observations and conclusions as a class. Expect students to look through the sunglasses and a polaroid film and figure out that the film must be oriented horizontally because sunglasses are vertically polarized. By doing this, they learn that polarized sunglasses change the light intensity.
(slide 11) Malus’ Law: Introduce students to Malus’ law and equation that relates the final light intensity based on incident light intensity created by the off-setting of two polarizing filters by angle θ. Malus’ law describes how the light intensity changes when polarized light passes through a second polaroid.
(slide 12) Quick Check: Distribute the handout to students and give them four minutes to complete it. Circulate the room as students work. Then go over the six questions as a class, having students share their answers first, before providing the answers.
(slides 13-14) Light Attenuation: Ask students to think about answers to the provided five questions before providing the answers. For the last question, give students 3-4 minutes to discuss options in their teams before sharing with the class. As necessary, scaffold a discussion to help students answer the questions. Record their answers on the classroom board.
Next, assign students the homework questions, as described in the Assessment section. Follow-up with the Exploiting Polarization: Designing More Effective Sunglasses activity for students to act as design engineers to creat their own optimized sunglasses product.
Lesson Background and Concepts for Teachers
Electromagnetic radiation refers to waves that propagate through electromagnetic fields. Essentially, electromagnetic waves are transversely oscillating electric and magnetic fields that travel at the speed of light: 3.0 x 108 m/s. Electromagnetic radiation is characterized into a continuous spectrum based on frequency/wavelength (see Figure 2).
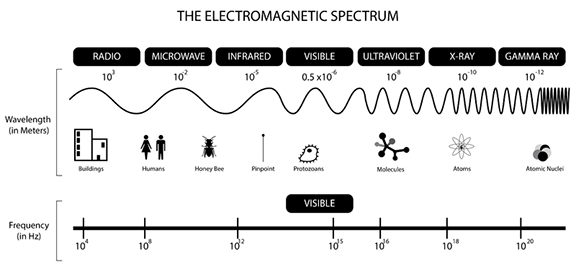
- We call the longest wavelengths or lowest frequency waves radio waves. They are responsible for the transmission of telecommunication data such as television, radio and cell phones. Within the band of radio waves are extreme high-frequency waves with wavelengths from 10 to 1 mm that are called millimeter waves, which are being evaluated to be used in next-generation cellular data service.
- Next in the spectrum are microwaves, which are radio waves of shorter wavelength, about 10 cm to 1 mm. Microwaves can penetrate into materials and transfer their energy below the surface, which is helpful for heating food. They are also often used in radar, satellite communications and wireless networks.
- Infrared waves are characterized by a larger frequency/shorter wavelength than radio waves and are mainly used in thermal imaging.
- Visible light is the smallest range of wavelengths/frequency of the spectrum that humans can detect with their eyes. Visible light contains the colors of the rainbow.
- The next range of wavelengths with higher frequencies/shorter wavelengths is ultraviolet radiation. Ultraviolet waves contain a lot of energy, but not enough to penetrate human bodies. Ultraviolet radiation can damage skin tissue, resulting in sunburns and sometimes skin cancer.
- X-rays have shorter wavelengths or larger frequencies than UV radiation and carry enough energy to penetrate human bodies. They are mainly used in medical imaging.
- Lastly, gamma rays have the largest frequency/shortest wavelength of all electromagnetic radiation, therefore the most energy. Gamma rays are used with telescopes to explore space, to sterilize foods and seeds, for some diagnostic medical imaging, and sometimes for radiation cancer therapy.
The energy of an electromagnetic wave is directly related to its frequency. Since frequency is inversely related to the wavelength, electromagnetic energy behaves in the same fashion. As the frequency of electromagnetic radiation increases, so does the amount of carried energy.
Light—just like all electromagnetic waves—propagates through the electromagnetic fields. Light polarization refers to the alignment of the field disturbances. Light is unpolarized when it vibrates in more than one direction. Light that is emitted from light bulbs, the sun or a candle flame is unpolarized.
It is possible to convert unpolarized light to polarized light through multiple methods: transmission, reflection, refraction and scattering.
- Polarization through transmission is when light passes through a special filter that blocks a specific direction of electromagnetic vibration. This filter is usually called a polaroid.
- Polarization through reflection happens when light hits a non-metallic surface. As light hits the surface plane, the vibrations increase in the same plane, making the light become polarized in that direction.
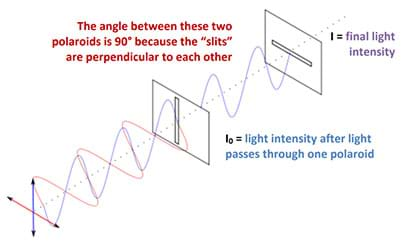
The most common way to polarize light is to use a polaroid filter. Polaroid filters are chemically designed to permit only a specific plane of polarization to pass through (remember this is for simplification), as is illustrated in Figure 3.
When unpolarized light enters a polaroid filter, the light intensity outputs at half as much as it originally was. The alignment of a polaroid filter is called its alignment axis. Polarized light can be polarized again, through one of the methods mentioned earlier. As the light becomes polarized again, its intensity decreases, as described by Malus’ law:

where I is the light intensity after it becomes polarized a second time, I0 is the light intensity after the first polarizer, and θ (theta) represents the angle between the two polarizers.
When the two polaroids are perpendicular to each other, the intensity is 0 W/m2; see Figure 4 as an example. In this case, the angle between the directions of the first and second polaroids is 90˚. When this is substituted into Malus’ law, cos90˚ = 0, which makes the overall final light intensity 0 W/m2.
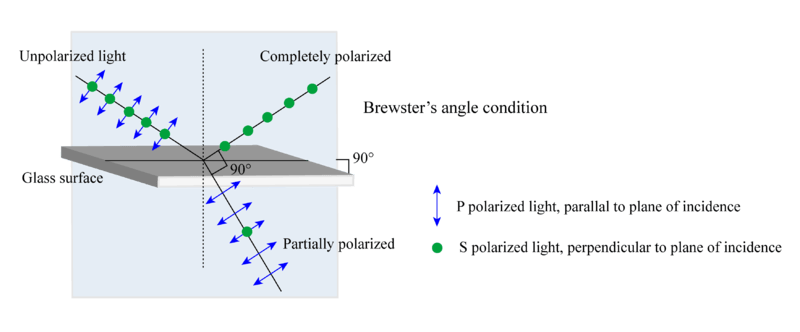
Unpolarized light can also become polarized through reflection off non-metallic surfaces such as a road or water. The extent of polarization depends on the material and the angle at which the incident light strikes its surface. If the light is incident at the polarization angle, also known as Brewster’s angle, then light is perfectly polarized. Brewster’s angle is dependent on the indices of refraction of the two materials. It is calculated by:
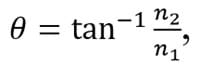
where n2 is the index of refraction of the medium on which the light is hitting and n1 is the index of refraction of the medium on which the light is originally traveling. Typically, light is polarized in the direction parallel with the surface. For instance, if light reflects off of road asphalt, it becomes horizontally polarized, which results in glare when looking at objects through their reflections, as illustrated in Figure 5. By blocking the plane of polarized light, the glare is reduced; that is why the polarization axis of most sunglasses is vertical.
Attenuation is the reduction of intensity of any electromagnetic wave. Electromagnetic radiation attenuates as it passes through different mediums. Both medium and frequency affect how much radiation is attenuated. Sunglasses attenuate sunlight, lead attenuates x-rays, and human bodies attenuate the millimeter wave. The attenuation of electromagnetic waves is due to the absorption and scattering of photons. Some electromagnetic wavelengths are more absorbent than others through different mediums. The frequencies of ultraviolet light, for instance, have very little attenuation through plastic. However, those same frequencies are nearly completely attenuated, or blocked, by using chemicals such as titanium dioxide or zinc oxide.
Instead of visible light and ultraviolet radiation, radio waves are currently being studied in the creation of the 5G data network. The plan is for this network to use 60 GHz radio waves to increase the wireless capacity for data sharing. However, this particular frequency is easily attenuated through the atmosphere, buildings and people. To address this, engineers suggest the use of multi-directional antennas to guide the beams around the blockages. Since electromagnetic waves travel in straight lines, many more antennas will be required in order to reroute the beam in 5G networks.
Associated Activities
- Exploiting Polarization: Designing More Effective Sunglasses - Working as if they are design engineers, students use a light sensor to measure the characteristics of inexpensive, unpolarized sunglasses—the light intensity and UVA/UBV attenuation. Then teams use their own combinations of the provided materials to design and create their own prototype sunglasses that improve upon the original pair by reducing more light and blocking UBA/UVB radiation. After testing and refinement, teams create advertisements to sell their products, using data and graphs to support their claims.
Vocabulary/Definitions
attenuation: The reduction of amplitude of a signal, electric current or other oscillation.
electromagnetic radiation: Waves of the electromagnetic field propagating through space and carrying electromagnetic radiant energy.
light intensity: Essentially, the brightness of light. Intensity is directly related to the energy of light. The rate at which light is received at the surface.
opaque: A material characteristic that blocks the passage of radiant energy. Not transparent or translucent. Not allowing light to pass through.
polarization : Alignment of vibrations in a transverse wave—a wave in which the disturbance is perpendicular to the direction of movement.
polaroid: An optical filter that permits light waves of a specific polarization to pass through while blocking other polarizations. Polaroids can convert beams of light of mixed polarization into well-defined polarizations.
translucent: A material characteristic that transmits and diffuses light so objects on the other side of the medium are not clearly seen.
transparent: A material characteristic that transmits light to completely pass through, so objects on the other side of the medium can clearly be seen.
Assessment
Pre-Lesson Assessment
Bell Work: Sunglasses Analysis: Direct student teams to each carefully examine two pairs of sunglasses, one polarized and one unpolarized. In groups, students compare and contrast them, then share their observations in a class discussion during which their ideas are organized into a two-part Venn diagram in order to arrive at the conclusion that the key difference is that the polarized sunglasses enable you to see a sharper image.
Post-Introduction Assessment
Mini-Activity: During the How Do Sunglasses Work? Presentation, groups each use two polaroid filters and make observations about what happens to light intensity as light passes through just one and then a combination of the two filters. They are directed by three questions on slide 8. Go over students’ answers as a class to gauge their comprehension of the material about polarization by transmission.
Lesson Summary Assessment
Quick Check: Midway through the How Do Sunglasses Work? Presentation (at slide 12), have students answer the six questions on the Quick Check Handout. Students may refer to their notes from the slides. Review their answers to gauge their knowledge of Malus’ law to calculate transmitted intensity, tinted vs. polarizing filters, and how light becomes polarized.
Homework
Homework Problem Set: Assign students to answer the seven questions in the How Do Sunglasses Work? Homework. Students individually demonstrate their knowledge by calculating light intensity as it passes through multiple polaroids, comparing and contrasting tinted and polarizing filters, and evaluating the attenuation of waves through various materials. The last question poses a hypothetical design problem (sunglasses design project), which connects the lesson to its associated activity. Permit students to research their answers, citing source materials.
Lesson Extension Activities
As an extension, have students examine sunscreen ingredients to determine how the ultraviolet frequencies attenuate through each ingredient. Assign them to research which is the active ingredient that protects skin.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn the basic properties of light — the concepts of light absorption, transmission, reflection and refraction, as well as the behavior of light during interference. Lecture information briefly addresses the electromagnetic spectrum and then provides more in-depth information on visible li...

Student groups rotate through four stations to examine light energy behavior: refraction, magnification, prisms and polarization. They see how a beam of light is refracted (bent) through various transparent mediums. While learning how a magnifying glass works, students see how the orientation of an ...
References
“The Electromagnetic and Visible Spectra.” Light Waves and Color – Lesson 2 – Color and Vision, The Physics Classroom. Accessed July 19, 2017. http://www.physicsclassroom.com/class/light/Lesson-2/The-Electromagnetic-and-Visible-Spectra
“Polarization.” Light Waves and Color – Lesson 1 – How Do We Know Light Is a Wave? The Physics Classroom. Accessed July 19, 2017. http://www.physicsclassroom.com/class/light/Lesson-1/Polarization
Rappaport, Theodore S. (2013) NYU WIRELESS. Publication Library, Tandon School of Engineering, NYU. http://wireless.engineering.nyu.edu/
Rappaport, Theodore S. “Millimeter Wave Mobile Communications for 5G Cellular: It Will Work!” (PowerPoint® slide presentation) NYU Wireless and IEEE. http://pimrc2014.ieee-pimrc.org/IEEE%20PIMRC%20Keynote%20Sept%205%202014%20Final%20Ted.pdf
Rappaport, Theodore S., Shu Sun and Rimma Mayzus. “Millimeter Wave Mobile Communications for 5G Cellular: It Will Work!” IEEE Access, Vol. 1, No. 1, pp. 335–349, May 10, 2013. (includes five-minute YouTube video) http://ieeexplore.ieee.org/document/6515173/
Copyright
© 2018 by Regents of the University of Colorado; original © 2017 Michigan State UniversityContributors
Adam Alster; Quan Tran; Drew KimSupporting Program
Smart Sensors and Sensing Systems RET, College of Engineering, Michigan State UniversityAcknowledgements
This curriculum was developed through the Smart Sensors and Sensing Systems research experience for teachers under National Science Foundation RET grant no. CNS 1609339. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: June 6, 2019








User Comments & Tips