Hands-on Activity Acting Like an Algorithm

Learning Objectives

After this activity, students should be able to:

• Explain how the PageRank of a website is determined.
• Understand the general concept of an algorithm, as well as its capabilities of making calculations fast and easy.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• two clear cups
• random selection tool, such as a bag with colored pieces of paper; students draw one piece randomly from the bag when they need to choose a random color
• 20 pom poms, created from yarn, or an equivalent item that can be used for counting (these items do not need to be unique to every group);

To share with the entire class:

• ball (soft like a tennis ball)
• strings of yarn
• pipe cleaners for arrow heads, shown below in Figure 1 (optional)

Worksheets and Attachments

Pre-Req Knowledge

Students should have an understanding about the logic behind Google’s PageRank algorithm, covered in the associated lesson, Algorithms and Everyday Life.

Introduction/Motivation

Scientists and engineers must make use of their time wisely. Algorithms help optimize the time required to complete a task by finding and programming the quickest path to get something done. Take, for example, brushing your teeth. Many of us have a specific routine that we follow when brushing our teeth, so we don’t even need to think about it. Our brain is programmed to naturally follow those specific steps that we created for routine. Algorithms can be used in order to sort a large set of information based on a set of structural rules, or step by step instructions.  For example, usually when you search for something on Google, there are many results, even pages upon pages of results. However, more often than not, you never have to venture off that first page of results, because the most important and relevant items, are on that first page. This is because of a specific algorithm that Google uses to sort through and figure out which websites are the most important.

In the accompanying lesson, Algorithms and Everyday Life, we talked about the logic behind PageRank: websites with links from other important websites are deemed to be the most important. To compute PageRanks, Google uses a very clever computer program that is based on mathematical concepts from a field called “linear algebra”. Linear algebra is a topic that is used widely throughout science and engineering and is taught in college.

In this activity, we’re not going to talk about linear algebra or the actual steps inside Google’s algorithm. Instead, it turns out there is a very fun trick we can use to come up with the same answer as Google’s algorithm. This trick involves simple concepts of probability and randomness. By playing a game, we can determine which websites in a network have the highest PageRank.

I am going to present a couple models in which we will replicate by dividing into groups.

Procedure

Background

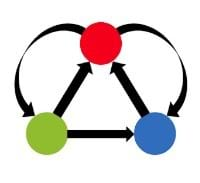
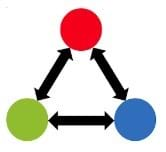
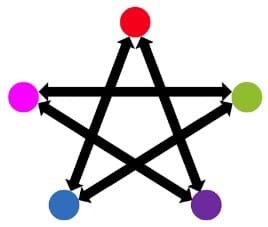
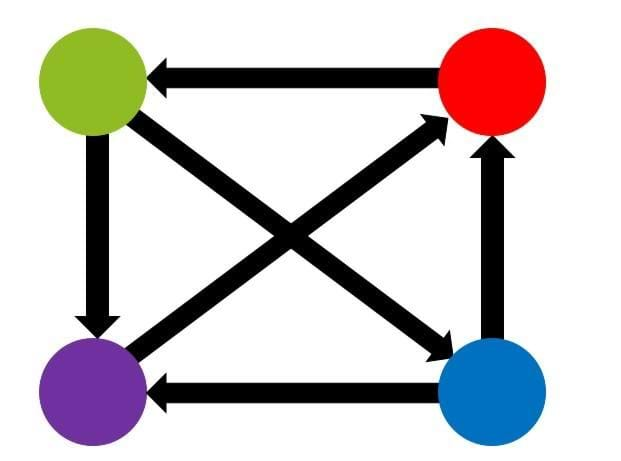
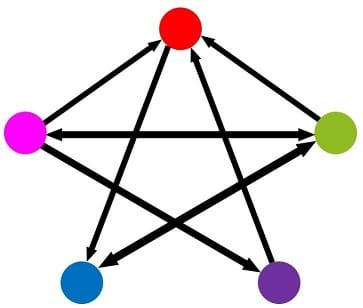
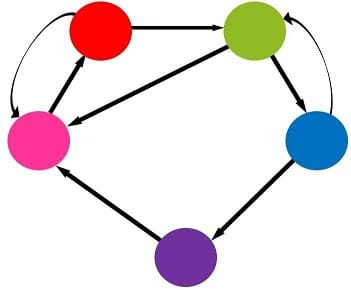
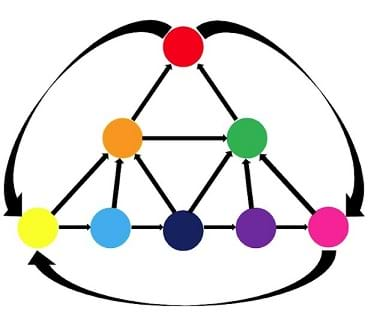
The students will engage in a simple ball game that produces equivalent results to that of the Google PageRank algorithm. Each slide shows a network model (see Figure 2 for an example corresponding to three websites).  In this example, students will break into an equivalent number of groups, in this case three; call them red, green, and blue to correspond with Figure 2. The groups will arrange themselves in the room to correspond with what they see in the diagram and will use yarn stretching from one group to another to indicate a “link” between those two groups. In the case of Figure 2, there would be yarn from the red group to both green and blue groups, and there would be an arrowhead made of pipe cleaner at one end of each link to indicate its direction. Similarly, the blue group would only have one link going out, which would connect to the red group.

Each group will be given two cups; one empty cup and one filled with 20 pom poms. Students will play a game where a ball is tossed around the room, but the ball must follow the links shown in the network diagram. For example, in the case of Figure 2, the red group can throw to either the green or blue groups, but the blue group can only throw to the red group. Each group will keep a count of how many times they receive the ball, by moving one pom-pom each time into the empty cup. When any group runs out of pom poms, the game will end.

A key to this game is that each group must randomly choose which group to throw the ball to next, based on the other groups it links to. This is where the random selection device is used, for example: the red group may have a bag containing one green and one blue piece of paper. Each time they receive the ball, they pick a piece of paper randomly from the bag and throw the ball to that group. Then they replace the paper in the bag. This helps to ensure that groups are being randomly chosen, and students are not playing favorites.

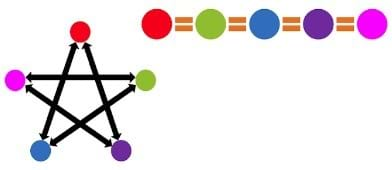
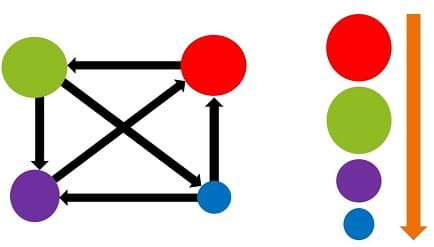
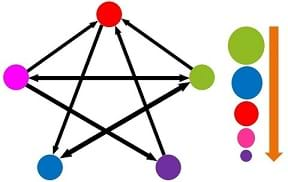
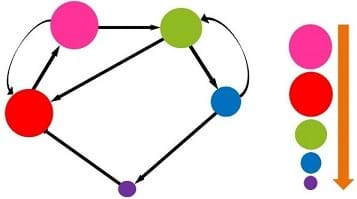
When the game ends, the students can compare how many times each group received the ball, by comparing how many pom-poms they have put into their empty cups. The groups with the most pom-poms will correspond to the websites with the highest PageRanks, and vice versa. Getting perfect results could require playing for a very long time, but if the game ends when one group has received the ball 20 times, that is generally enough to get a good approximation of the true relative PageRanks.

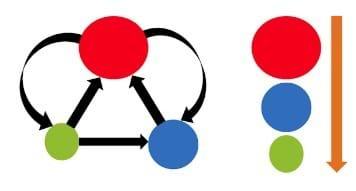
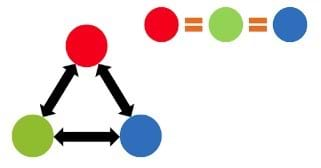
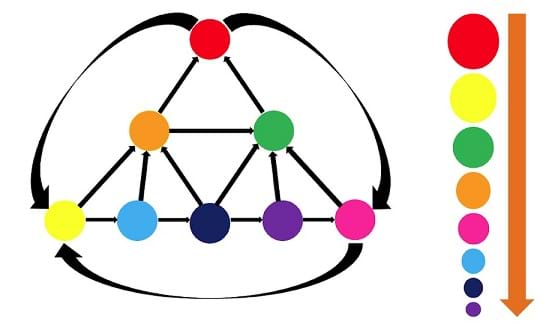
Figure 3 shows the true results for the network from Figure 2. On Figure 3, the sizes of the circles represent their relative importance, and on the right side of the slide they are ordered from highest PageRank (top) to lowest PageRank (bottom). In this case, the red website will have the highest PageRank (they should receive the ball the most times), and the green website will have the lowest PageRank (they should receive the ball the fewest times). It is interesting to discuss with students why this should be the case when looking at the network diagram, and also to have the students try to guess the relative rankings before the game begins.

Before the Activity

• Present the Algorithms and Everyday Life lesson.
• Decide whether to show the Acting Like an Algorithm (for Higher Levels) PowerPoint or the Acting Like an Algorithm (for Lower Levels) PowerPoint, depending on student ability.
• Create at least 16 arrows with yarn and pipe cleaners: tie pipe cleaner arrows to long pieces of string.
• Create 20 pom poms with yarn.
• Create a random selection tool (such as different colored pieces of paper in a bag) for each group, for each activity based on the activity images given on the slides.

For example, if students are acting out the network model of Figure 2, the red group could use a random selection tool with green and blue colored paper.

With the Students

1. Set up the Acting Like an Acting Like an Algorithm (for Higher Levels) PowerPoint or the Acting Like an Algorithm (for Lower Levels) PowerPoint. (The slides include paired activity set-up and results slides.)
2. Divide students into groups based on the images given on the PowerPoint slides; each color dot on the slide should correspond to one group.
3. Give each group a cup already filled with pom poms (it’s good to give each group the same number), and an empty cup with their group color to fill with pom poms, and a random selection tool to determine which group toward which they will throw the ball.
4. Have groups hold string with pipe cleaner arrows to show “connected” groups, as indicated by the PowerPoint slide.
5. Pick a group to start with the ball.
6. Have the first group choose randomly which group to throw to, depending on which other groups they are linked up to.
7. Once the group has chosen, have them throw the ball to that group.
8. The group that receives the ball will place a pom-pom in their empty cup, then repeat steps 4 and 5.
9. Continue the game until any group runs out of pom poms from their supply cup.
10. Have the students line up their colored cups and compare to see how the groups were ranked from most to least.
11. Show and compare the slide with the algorithm’s calculated results with the students’ generated activity. On the slides with results, the sizes of the circles represent their relative importance, and on the right side of the slide they are ordered from highest PageRank (top) to lowest PageRank (bottom).
12. Repeat steps 2 through 10 for the following activity slides in the PowerPoint. There are four activities for students to act out in each level PowerPoint. Figures 2 through 9 show the activity/results images for lower level audiences; Figures 6, 7, and 10 through 15 show the activity/results images for higher level audiences.

Follow Figures 2 through 9 below for lower levels:

Follow Figures 6, 7, and 10 through 15 for higher level audiences:

Vocabulary/Definitions

algorithm: A set of instructions a computer program uses to carry out various tasks to make life easier for scientists and engineers.

PageRank: An algorithm used by Google to sort through various web pages on a web search.

probability: How likely a specific outcome or event will happen.

relativity: How similar or in relation one thing is to another.

Assessment

Pre-Activity Assessment

Probability Prediction: Ask students: “Which group do you think will receive the ball the most? Which group do you think will receive the ball the least?”

• Possible Answers:  Students should make their own predictions to this question. Possible responses could include: “What lead you to those decisions? Let’s see if your predictions are right!” Students might guess that the groups having the fewest incoming links will receive the ball least often, but this is not the case. For example, in Figure 14 the red node has only two incoming links, while the orange node has four incoming links. Yet in the long term, the red node will receive the ball the most.

Activity Embedded Assessment

Networking Assessment: As students go through the different Activity slides, tell them: “Think about how websites go through this process. How many times your group catches the ball is dependent upon what other groups you are connected to. If you only have one link connected to your group, there is a slim chance your group will end up with the most pom-poms, unless the only group you are connected to has many links. The group that ends up with the least amount of pom poms would represent an unpopular website. Before we finish the game, which group seems to be the most popular? What about the least popular, and why?”

• Possible Answers:  Students should make their own inquiry on this question. There are no right or wrong answers! The highest-ranked websites will generally be those with the most links from other highly-ranked websites.

Post-Activity Assessment

Group PageRank Assessment: Have the kids compare each of their pom-pom filled jars. Were they right about their predictions? Have them discuss as a class to try and explain why they were right or wrong.

Algorithm Comparison: If the results of the activity don’t match the results that the actual algorithm came up with, ask the students why they think we were not able to come up with matching results.

• Possible Explanation: We modeled an algorithm that gains results based off an iterative (or repetitive) process. This means that the more this process is played out, the more accurate the results we will be able to achieve. Since we are only human, we are only able to repeat this process until we get tired of doing it. The algorithm that we modeled our game off of is able to do this same process an infinite number of times, therefore achieving much more accurate results. The real PageRank algorithm uses a mathematical shortcut, which boils down to the use of linear algebra equations and processes that compute the eigen values of a matrix in order to come up with these numbers.

Troubleshooting Tips

• If results don’t turn out exactly as expected, explain to students that we are only able to play the game until we run out of pom-poms, whereas the algorithm used to compute the result the ranking order iterates through this process an infinite number of times. Express why this makes algorithms so important to scientists.
• The yarn with arrow heads is not necessary for the activity; however, it helps the students visualize what’s going on.
• Depending on how many students there are in a classroom, the group numbers can be modified to fit the class.
• Prepare the activity beforehand, setting all the elements up correctly takes a little bit of time, and should not be done on the spot.

Activity Extensions

• Have the students come up with their own models to test. Compare the results of the student’s created model to the model generated on a website that is able to determine the PageRank of the different groups, such as this PageRank Simulator.

Activity Scaling

• Cater the group sizes to your classroom. Try to have no more than 3 students to a group, so every student in a group may have their own job. (One student catches the ball, one randomly picks the group to throw to, one adds a pom-pom to the jar when necessary.)
• For lower grades, use the Algorithms and Everyday Life (for Lower Levels) PowerPoint that was intended for younger students. Use the figures intended for younger students for the activity. The activities for younger students involve less nodes in each of the activity figures to make the probability aspect more comprehensible for younger students.
• For higher grades, use the Algorithms and Everyday Life (for Higher Levels) PowerPoint that is intended for older students. Use the figures intended for older students for the activity. The activities for older students involve more nodes in each of the figures to make guessing the probability of each group’s PageRank harder to estimate.

Copyright

Contributors

Supporting Program

Acknowledgements

This curriculum was based upon work supported by the National Science Foundation under CAREER Grant CCF-1149225, NSF Grant CCF-1409258, and NSF Grant CCF-1704204 through the Colorado School of Mines. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.