Lesson Algorithms and Everyday Life

Learning Objectives

After this lesson, students should be able to:

• Explain what algorithms do and how they are useful to us.
• Understand what a website network is, and the relative importance of websites.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Worksheets and Attachments

Introduction/Motivation

[Show students the attached PowerPoint. Choose between Algorithms and Everyday Life (for Higher Levels) PowerPoint and Algorithms and Everyday Life (for Lower Levels) PowerPoint, depending on the level of students.]

In a digitally dependent world, who are the magicians behind the scenes making all of this technology possible? The answer is scientists and engineers. There are many factors that go into the extensive process of making our modern-day technology possible, but one important tool that scientists and engineers use are algorithms. The word ‘algorithm’ might seem scary at first, but it is actually a straightforward concept. People use algorithms all the time in their daily routines for accomplishing tasks, such as brushing your teeth, or making a sandwich!

[The PowerPoint Presentation Script provides a copy of the directions for both PowerPoints. The directions for the Algorithms and Everyday Life (for Higher Levels) PowerPoint are reproduced below.]

• Slide 1: What are algorithms?

Put very simply, algorithms are a set of step-by-step instructions. In the realm of computer science, algorithms are a specific set of instructions and operations that a computer program carries out to accomplish various tasks. For example, a user of a computer program could be asked to enter in 3 random numbers. The program could then follow a set of specific steps in order arrange the numbers from smallest to largest.

Examples of said steps:

• Ask the user to enter 3 numbers. 
• Look at the numbers in the order that the user entered them.
• Is the first number larger than the second number?
• If so, swap the 2 numbers.
• Otherwise, do nothing.
• Is the second number larger than the third number?
• If so, swap the second and third number
• Otherwise do nothing.
• Repeat steps 2-4 until correct order is achieved
• Return new sequence to user

• Slide 2: Why are algorithms important?

o   Scientists and engineers have to make use of their time wisely. Well-built algorithms help optimize time by finding and programming the quickest path to get something done. For example, Instagram uses an algorithm which determines which posts to show you at the top of your feed, based on your browsing habits. This way, you spend less time looking for posts that you might be interested in. Algorithms can be used to sort a large set of information based on a set of structural rules, such as step by step instructions.  For example, usually when you search for something on Google, there are many results, even pages and pages of results. However, more often than not, you never have to venture off that first page of results, because the most important and relevant items are on that first page. This is because of a specific algorithm that Google uses in order to sort through and figure which websites are the most important, based on relevance and website rank. We will go into further depth of this specific algorithm later on.

• Slide 3: First let’s look at a real-life example of an algorithm for a task that doesn’t require a computer at all: making a grilled cheese sandwich. When you make a grilled cheese, you generally follow specific steps to reach the desired outcome. First you need bread, as shown in Figure 1. Then you need to butter the bread, as shown in Figure 2. Cheese is then added, as shown in Figure 3. The final step is to cook the grilled cheese, as shown in Figure 4.

• Slide 4: Only upon completing all of these steps are you able to enjoy the final result, as shown in Figure 5. This is exactly how an algorithm works: it follows steps like these images below:

• Slide 5: Google PageRank is a more complex example of an algorithm. This is the algorithm that Google uses to determine the importance of a website, based on how many websites are linked to that website.

The algorithm assigns each webpage a number, called a PageRank (or PR), on a scale from 1 to 10. Higher numbers correspond to higher importance, which means the higher that webpage will appear in search results.

• Slide 6: The PR is one of the main factors that Google uses to determine what order to show you the search results when you search for a website. Another important factor is relevance. For example, if I were to search for “soccer”, as seen in Figure 6, notice how there are no pictures of bananas in the search results. This is because bananas are not relevant to my search query, but soccer balls, soccer players, and soccer fields are relevant.

In general, Google shows you the most relevant and highest PR websites first. Relevance is actually computed by a separate algorithm used by Google that aids to organize data. The higher a website’s PR is, keeping the relevance of the search in mind, the higher it will be in the search results (if it is relevant to your query).

How does Google determine which websites are the most important, and deserve the highest PR? Interestingly, this is based on looking at how all of the websites link to each other. As you know, when you are visiting a website, you will often see links to other websites. A website reviewing bicycle helmets might include links to Amazon, where you can buy those helmets. An article about a soccer team might include links to ESPN bios for each player. And so on.

In general, important websites should be those that have lots of other websites linking to them. However, PageRank does not merely involve counting how many links are coming into each website. Instead, PageRank says that important websites should be those that have lots of other important websites linking to them.

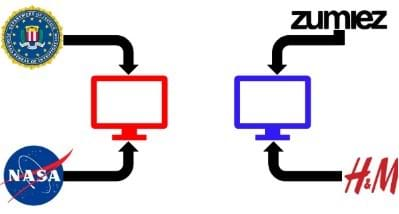
• Slide 7: Consider the example in Figure 7. There we see two websites (one in red and one in blue), each with two other websites linking to them. However, the red website has two very important government websites linking to it, whereas the blue website has two less important online shopping websites linking to it.

• Slide 8: So, in this case, Google’s algorithm should assign a higher PR to the red website. Importance of a website is determined by credibility of that website. Credibility here means how likely it is that the information you are gaining from that source is true or not. For example, if I googled “what kind of fabric are astronaut suits made of?”, Google would give NASA a higher page rank because they would be a more credible source for that information than a clothing store would be.

• Slide 9: Examples of different PRs. Notice how Facebook and YouTube have perfect PageRanks, while the website for the Sweetbriar only has a PR of 1. This is because websites like Facebook and YouTube have many other important websites linking to them, while the Sweetbriar website is from a small organization, so significantly fewer websites link to its website. Warning: Note that a high PR does not automatically mean that a website has good information or is necessarily more credible. All of this is simply determined by which websites link to which other ones.

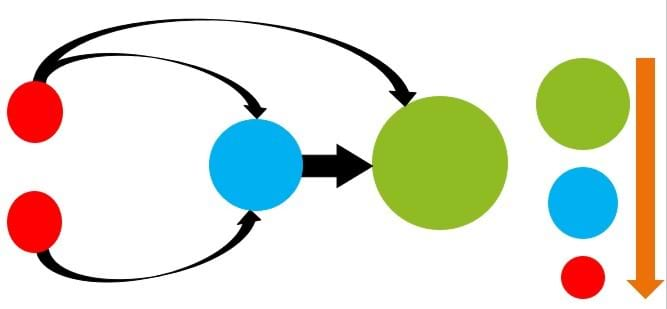
• Slide 10: Figure 8 shows an example of how PR can be determined simply by looking at which websites link to which other ones; these links define how they are connected in a network. In this example, pretend that each circle represents a website, and the arrows represent links from one website to another. Scientists and engineers often use pictures like this to understand networks of interacting machines, websites, etc. So, in this example, both red websites link to the blue one, one red website links to the green one, and the blue website also links to the green one. In this example, the red websites should have the lowest PR, since no other websites link to them. This is indeed the case, and so the red circles are drawn to have the smallest size (the size of each circle represents its PR). The blue website is the next largest (next highest PR), since it has links from two red websites. And the green website is the largest (highest PR) of them all, since it has links from one red and one blue website.

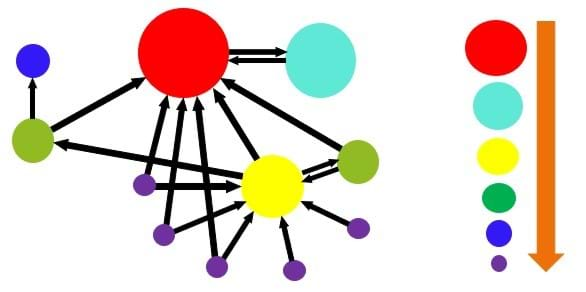
• Slide 11: This can quickly become very complicated! Figure 9 shows a more complex example of a network of websites. Here, the yellow circle has 6 links coming into it, whereas the light blue circle only has one link coming into it; so why does the light blue circle have a larger PR than the yellow circle? It is because the one link to the light blue website is from the red website, which has the highest PR among all of them. This is more important than all of the links to the yellow website from other websites with low PR. Another thing to note is that the number of links coming out of a website does not affect its PR.

• This leads to an interesting problem: to determine a website’s PR, you need to know the PR of the websites that link to it. But to determine the PR of those sites, you need to know the PR of all the websites that link to those, and so on creating a vast hierarchy of interconnected links. This seems like a never-ending process.
• To compute PageRank, Google actually uses a very clever computer program that is based on mathematical concepts from a field called “linear algebra”. Linear algebra is a topic that is used widely throughout science and engineering and is taught in college.
• This lesson continues with an associated activity called “Acting Like an Algorithm”. In that activity, we’re not going to talk about linear algebra or the actual steps inside Google’s algorithm. Instead, it turns out there is a very fun trick we can use to come up with the same answer as Google’s algorithm. This trick involves simple concepts of probability and randomness, combined with the iterative process of a ball game. By playing a game, we can determine which websites in a network have the highest PR.

Lesson Background and Concepts for Teachers

Google PageRank is a way to measure the importance of a website, based on how many other websites are linked to it. This allows Google to place credible websites towards the top of search results and give less attention to the less credible sites. PageRank is useful for both users as well as website owners/companies. Users are able to benefit by gaining ease of access to reliable websites. Companies benefit if their website is on the first page of search results, because users are more likely to visit their webpage.

Put simply, the PageRank of a website can be thought of as a specific ranking for a website between the values of 1 and 10. Websites with a PageRank of 1 can be considered as unimportant websites, and websites with a PageRank of 10 can be considered as really important websites. Each link that a website has leading to it from another webpage, can be considered as a ‘vote’ towards that website’s ranking. For example, if you were to google the term “Ice cream”, you might find a blog that has a link to the Häagen-Dazs website. You might have also found a website for a popular ice cream shop near you, which also has a link to Häagen-Dazs on their website. The more links that Häagen-Dazs has on other websites, leading to their own website, the higher their PageRank will be.

However, not all ‘votes’ are considered to be equally valuable. Websites with a PageRank of 10 carry much more weight when they link to another website, than when the link is coming from a website with a PageRank of 1.  A website with a high PageRank will contribute more to a website that it’s linked to than a website with a lower PageRank will. In general, a government website will have a higher PageRank, because of credibility (good sources come from websites like these, and thus more people are likely to reference this kind of credible source). If a government website, such as NASA, were to have a link to the Häagen-Dazs website, somewhere on their webpage, this link would count much more towards Häagen-Dazs’ overall PageRank, than a link coming from a blog website.

Considering the last example, a website might only have two pages linking to it, yet have a higher PageRank than a website that has 10 websites linking to it. This is possible because the two pages that the first website has linking to it, have much higher PageRanks than that of the 10 websites linking to the second website. Since credibility and reliability are important concepts in Google PageRank, this idea is crucial upon determining the overall PageRank of a website.

Keeping all of the past examples in mind, the actual calculation of a website’s PageRank can get tricky. Not only do we have to know how many web pages link to a website, but also the individual rank of the websites that are linking to the site. Considering this process, the actual calculation could be seemingly never-ending. Luckily, this is where algorithms come into play. Google PageRank uses a simple algorithm based on the mathematical concept of linear algebra. That algorithm is able disregard the value of other pages linking to a website, and instead uses a normalized link matrix and looks at the principal eigenvector of that matrix. This algorithm is able to perform this calculation without knowing the values of the contributing websites because of the iteration process, which helps create the principle eigen vector associated with the matrix. The algorithm loops over this same process a numerous amount of times, only stopping when the results of the calculation start to level out and show consistency between values.

This is one important aspect to keep in mind while having students perform the associated activity. Students will perform a process, in the form of a ball game, in which is reminiscent of the process that the PageRank algorithm follows. However, being that we are only human, we can only play this game for so long. The algorithm associated with Google PageRank is able to run this kind of process almost an infinite number of times, therefore the algorithm can and will achieve much more accurate results for the ranking process.

Associated Activities

• Acting Like an Algorithm - Students engage in an activity which symbolizes the Google PageRank algorithm. Students divide into groups and follow specific steps, in the form of a ball game, in order to match the results of the Google PageRank algorithm. They will gain a general understanding for the functionality of networking on the internet and be able to visualize the fundamental importance of algorithms, which can make calculations fast and easy.

  Watch this activity on YouTube

Vocabulary/Definitions

algorithm: A set of instructions to be followed, specifically by a computer.

Google PageRank: An algorithm Google uses to determine the relative importance of websites.

infinite: Does not stop, goes on forever.

probability: How likely a specific outcome or event will happen.

relevance: How similar or in relation one thing is to another.

Assessment

Pre-Lesson Assessment

Knowledge Inquiry: Ask the students if they have ever heard of an algorithm before. For the students that have, ask them to try and explain what it is.

• Possible answers: A math equation, something a computer program follows, something that follows steps.

Post-Introduction Assessment

Knowledge Inquiry: Get students thinking with a discussion around the question: Can anyone give me an example of a real-life algorithm?

• Possible answers: Anything that is accomplished by following steps.

Lesson Summary Assessment

Algorithm & PageRank Inquiry: Ask students questions to get them thinking about what the lesson covered.

Ask students: Now can someone who didn’t have an idea for an algorithm tell me what it is? Why are they important?

• Possible answers: An algorithm is something (a program) that follows steps. They are important because they can perform the same calculation an infinite amount of times, which allows for more reliable results.

Ask students: What is one factor that goes into determining the PageRank of a website (what determined the size of the circles in the different diagrams)?

• Possible answers: 1. The number of links going into a website (number of arrows going into a circle).

2. How important the links coming into a website are (size of the circles pointing to that circle).

Homework

Reflective Thinking: Have the students go home and come up with at least two “real life” algorithms, such as the example with the grilled cheese.

Lesson Extension Activities

Have students write their own “algorithm” by writing, or illustrating, steps in order to accomplish a certain task.

Additional Multimedia Support

This website allows you to create your own PageRank models and test the outcome. Based on the number of links you create for each block, the website iterates through the blocks with an embedded algorithm that follows a similar process of the PageRank algorithm. Based on the results this algorithm finds, a PageRank is given to each block.

http://faculty.chemeketa.edu/ascholer/cs160/WebApps/PageRank/

References

Copyright

Contributors

Supporting Program

Acknowledgements

This curriculum was based upon work supported by the National Science Foundation under CAREER Grant CCF-1149225, NSF Grant CCF-1409258, and NSF Grant CCF-1704204 through the Colorado School of Mines. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.