Quick Look
Grade Level: 9 (8-9)
Time Required: 3 hours 15 minutes
(four 50-minute periods)
Expendable Cost/Group: US $22.00 See the Materials List for some lower-cost alternatives and the non-expendable (reusable) items needed.
Group Size: 2
Activity Dependency:
Subject Areas: Geometry
NGSS Performance Expectations:

| MS-ETS1-2 |
Summary
Students learn about geometric relationships by solving real mini putt examples on paper and then using putters and golf balls to experiment with the teacher’s pre-made mini put hole(s) framed by 2 x 4s, comparing their calculated (theoretical) results to real-world results. To “solve the holes,” they find the reflections of angles and then solve for those angles. They do this for 1-, 2- and 3-banked hole-in-one shots. Next, students apply their newly learned skills to design, solve and build their own mini putt holes, also made of 2 x 4s and steel corners.
Engineering Connection
Engineers solve geometry-based problems every day, and they use math and science to help them design and build many projects. As they work in their specific fields, engineers get to know the ins and outs of their disciplines in order to create the best design solutions. Often, the real-world implementation of designs and plans vary from the theoretical “on paper” calculations, so engineers always start with prototypes of their designs to test them, discover discrepancies, and then improve them and test again—a process called iteration.
Learning Objectives
After this activity, students should be able to:
- Use geometric tools, such as protractors and Miras, to measure and draw angles.
- Solve for unknown angles of triangles and reflections.
- Use geometry to solve mini putt examples.
- Apply geometry concepts and tools to design, solve and build their own mini putt courses.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ETS1-2. Evaluate competing design solutions using a systematic process to determine how well they meet the criteria and constraints of the problem. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Evaluate competing design solutions based on jointly developed and agreed-upon design criteria. Alignment agreement: | There are systematic processes for evaluating solutions with respect to how well they meet the criteria and constraints of a problem. Alignment agreement: | |
Common Core State Standards - Math
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Use appropriate tools strategically.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the attributes of design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Make formal geometric constructions with a variety of tools and methods.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use geometric shapes, their measures, and their properties to describe objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- protractor
- (optional) Mira
- graph paper and pencils
- straightedge, or ruler with a metal edge
- calculator
- measuring tape
- golf ball (a few can be shared among groups)
- putter (a few can be shared among groups)
- Putt Worksheet, one per student
- Project Requirements and Grading Rubric, one per group
- (optional) computers with Internet access to use GeoGebra to solve problems (instead of paper)
To share with the entire class:
- wood, 2 x 4-inch dimension for hole framing, such as an 8-foot length for ~$3 at Home Depot (see Figure 1); ~16 feet per group
- steel corner joints, ~4 per group, for hole framing, for ~$4 each at Walmart (see Figure 1)
- (if wood is not pre-cut) saw, for cutting wood (for teacher use)
- screws
- drills
Materials note: See Figure 1 for an example student-built mini putt hole made of wood and corner joints. This one-hole mini-putt configuration cost about $22 (~$16 for four joints, ~$6 for wood). Recycled wood and used corner joints work just as well and cost less. To further reduce costs, use hammer and nails instead of steel corner joints, or use duct-taped thick cardboard instead of wood.

Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_geotools_lesson01_activity1] to print or download.Pre-Req Knowledge
- Practice using a protractor, as provided in the associated lesson, Geometry Tools: Angles & Reflections.
- A familiarity with the steps of the engineering design process.
Introduction/Motivation
What do engineers really do? Well, we know that they design, test, create and improve new and existing structures and systems and products. But, it can be hard to understand exactly what engineers do because engineers don’t all do the same thing!
Some practicing engineers complete all phases of the creation process—from the seed of an idea to selling a product in the marketplace—while others are focused on doing just one portion of the design process in depth—such as testing prototypes.
And then, different engineers work on all sorts of different projects—from designing cars to dams to artificial limbs to smartphones to shampoos and bubble gum. Did you know that some engineers design adventure theme parks and mini golf courses? It’s true!
Today, we will take what we have already learned about geometry and geometry tools—such as protractors and Miras—and practice as if we are engineers who design mini putt courses.
How are golf courses and mini putt courses designed? Are they just randomly built areas of sod and AstroTurf with holes, or are math and science accounted for to make the holes challenging but beatable? In designing any golf course hole, engineers need to be creative as well as know how angles, reflections and physics interact. Take a look at this video. (Show students a 59-second video of the “Greatest Mini Golf Hole-in-One Ever,” at https://www.youtube.com/watch?v=b6ppbdJwuVw.)
Creativity alone does not produce products, such as fun mini golf courses. That is why engineers study math, geometry and science in depth. Engineers need to first learn the math and science concepts that relate to the problem they want to solve, then apply their knowledge to design sophisticated models and prototypes of the system or project. They know that their on-paper designs might not work the same or as intended in the real-world, so they test to find out what works and what can be changed. Engineers fail and mess up every day, but they know that failure is a crucial and necessary step to achieving success.
Procedure
Background
On the first day of this activity (Part 1; 50 minutes), students solve mini putt hole problems based on the provided teacher putting hole(s). For the rest of the activity (Part 2; 150 minutes), student groups create their own mini putt holes and problems/solutions to share with the class.
Teacher Instructions and Tips for Making the Mini Putt Holes
- Either use the one of the two example provided hole layouts in the Example Hole Designs and Keys for Teacher, or design your own—but only what you can build; no need to complicate the designs (see Figure 1).
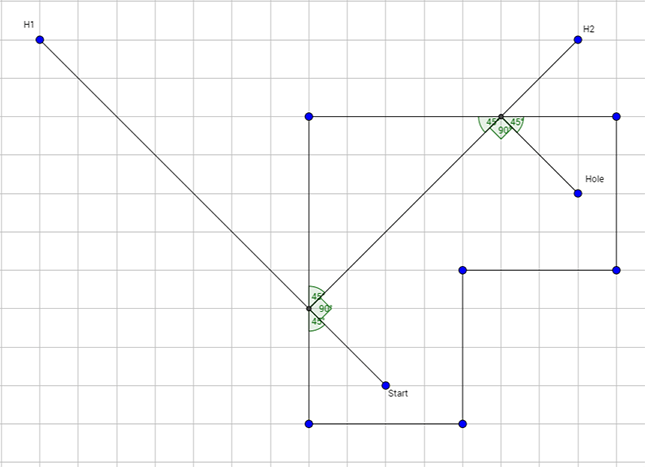
- Once designed, make keys for how to complete each hole with 1-, 2- or 3-banks (ball movement that reflects off the perimeter walls one, two or three times to make a hole-in-one). More than anything, to be able to solve the hole, students will need to know how to make the reflections.
- To simplify the process, use whole numbers (such as 3 feet, 4 feet) when scaling up the design.
- The holes may be simple with just a few walls or more complex with rounded edges and/or obstacles.
- Purchase 2 x 4s and corner joints to fabricate the holes and make precise 90° and 45° angles.
- If you want to have a drop-down hole, then you will need to elevate the hole somehow. Otherwise, it works fine to play on the level ground and use a post (or a plastic water bottle) for the hole; when a golf ball hits the post, it counts as having gone into “the hole.”
If desired, have students use GeoGebra to solve for the problems, rather than doing so on paper. Follow the GeoGebra links below, or refer to the Example Hole Designs and Keys for Teacher. To manipulate in GeoGebra, click the edit pencil in the top right corner, then click the new edit pencil just above the box diagram, and then scroll down to the edit applet. Then have students use the line segment tool, reflect point tool, and measure angle tool to solve problems following the same instructions.
Hole 1: http://ggbtu.be/mUKqXPMC8
Hole 1 Key
Hole 2: http://ggbtu.be/m3049151
Hole 2 Key
Teacher Planning for Day 1
- Gather materials and make copies of the Putt Worksheet.
- Design and build a set of mini putt holes (1-3 holes) for student use. See the instructions above.
- For Day 1, set up the (1-3) pre-made mini putt hole(s) throughout the classroom.
- You may want to prepare to use GeoGebra to show students a problem-solving example.
Teacher Planning for Day 2
- Gather building materials for student teams to construct their own mini putt holes.
- Decide what requirements you want teams to incorporate into their own hole designs, such as hills, bumps, islands, sand pits, angled walls, requiring the ball to bounce off a wall to get a hole-in-one, etc. Modify the Project Requirements and Grading Rubric document to match your requirements and expectations, and make copies of it for a student handout. Or list the requirements on the classroom board.
- (optional) To foster a competitive angle to the project, add to the project requirements a “competition criteria” section so the “best in the class” expectations are clear. For example, the winning design(s) might be based on criteria such as creativity, use of geometric concepts, aesthetics, accuracy, etc.
With the Students: Part 1 (50 minutes)
- Administer the pre-activity knowledge check discussion, as described in the Assessment section.
- Present to the class the Introduction/Motivation content.
- Go through an example problem together. It is helpful to use GeoGebra to show an example.
- Hand out the worksheets and materials needed. Explain to the students what they will be doing today: You will apply what you know about geometry, angles and protractors to solve on paper how to make holes-in-one for these putt-putt golf holes you see in the classroom. That means finding 1-bank, 2-bank and 3-bank solutions for each hole. Then you will test your solutions by playing the holes with putters and golf balls.
- Divide the class into student pairs to work together as groups.
- Help students solve for each hole on paper.
- Direct students to solve the hole(s) by finding the reflections of angles and then solving for those angles.
- Require them to complete 1-, 2- and 3-bank shots on each hole.
- Challenge problem: Solve a 3+ bank shot problem.
- Then review and approve their answers.
- Once they solve the hole(s) on paper, direct groups to play on the real hole(s) to see if their calculated (theoretical) paper solutions work. Have them make comparisons and observations.
- Help them complete the real-life holes by giving tips and asking questions. Example prompt: Why doesn’t the ball bounce at the same exact angle?
- Then have a competition for the best shot.
With the Students: Part 2 (150 minutes)
- Divide the class into student pairs to work together as groups to make their own mini-putt holes.
- Give students building materials and the challenge requirements.
- On blank paper, have student groups brainstorm some possible design options. *At a minimum, make sure the two hole designs used on yesterday’s worksheet are built by at least two groups, so that the built holes can be used to test their worksheet answers. *
- Approve the designs before building commences.
- Help students as needed with cutting and drilling.
- After the designs are built, test the holes. Then determine the winning team(s).
- Conclude by administering the post-activity exit ticket, as described in the Assessment section.
Vocabulary/Definitions
bank: When a ball bounces off a wall or surface.
incidence (geometry): The angle that an incident line or ray makes with a perpendicular to the surface at the point of incidence.
reflection: The angle made by a reflected ray with a perpendicular to the reflecting surface.
Assessment
Pre-Activity Assessment
Prior Knowledge Check: Start class with an open discussion to review topics from the Geometry Tools: Angles & Reflections associated lesson and answer questions. For one minute, ask students come up with questions on their own. Then have them discuss the answers with their neighbors or group. Important concepts for this activity include: reflection, point of reflection, angle of incidence, angle of reflection, angle of reflection is equal to the angle of incidence, angles on a straight line add to 180°, and how to use a protractor. As necessary, go through a few examples to demonstrate these concepts.
Activity Embedded Assessment
Worksheet: Have students complete the Putt Worksheet. Review their answers to look for concept comprehension and accuracy.
Post-Activity Assessment
Exit Ticket: Have students write down and explain the differences between the results they expected from their “on paper” calculations and the results they found in real-life putting, and what might cause the discrepancies. Have them hand in this written analysis as an exit ticket.
Investigating Questions
- Why doesn’t the ball take the same path as your paper solution predicted? (Answers: Wood imperfections, inelastic collision between golf ball and wood, approximations made when creating the model, slight errors in construction.)
- What would you need to have it work perfectly? (Answers: Ideal materials, frictionless surface, precise measurements.)
Safety Issues
- Remind students not to hit the balls too hard since they can easily bounce and hit others.
- Limit cutting and drilling to the teacher. Or, pre-cut wood to the desired lengths in advance.
Troubleshooting Tips
- To clear up any confusion, start with an example on GeoGebra.
- Having a grid on the real-life hole(s) helps to create connections for students. Do this by mounting string above the wooden edges of the mini-putt holes.
- Suggest that students only solve two problems per side of graph paper (such as 1- and 2-bank solutions); more than that results in a confusion of overlapping of lines.
Activity Scaling
- For lower grades, simplify the math by having them only solve for angles of incidence and reflection. Provide solved holes with bank shots, and have students measure the angles.
- For higher grades, use more algebra to solve the problems. Also, create word problems for students to complete. Create more complicated holes for students to attempt to solve.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn about common geometry tools and then learn to use protractors (and Miras, if available) to create and measure angles and reflections. This lesson prepares students to conduct the associated activity in which they “solve the holes” for hole-in-one multiple-banked angle solutions, make ...

Students learn about nondestructive testing, the use of the finite element method (systems of equations) and real-world impacts, and then conduct mini-activities to apply Maxwell’s equations, generate currents, create magnetic fields and solve a system of equations. They see the value of NDE and FEM...
Copyright
© 2016 by Regents of the University of ColoradoContributors
Russell Anderson; Malinda Zarske; Andi Vicksman; Ryan Sullivan; Maia Vadeen; Nathan Coyle; Aaron Lamplugh; Devin RourkeSupporting Program
CU Teach Engineering (a STEM licensure pathway), Engineering Plus Degree Program, University of Colorado BoulderAcknowledgements
This activity was developed by CU Teach Engineering, a pathway to STEM licensure through the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.
Last modified: January 9, 2020






User Comments & Tips