Lesson Geometry Tools:
Angles & Reflections

Learning Objectives

After this lesson, students should be able to:

• Use geometric tools to measure and draw angles.
• Describe how to reflect points and lines using a geometry tool.
• Explain how engineers use geometry tools to design everyday products and infrastructure.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Worksheets and Attachments

Pre-Req Knowledge

A familiarity with angles—what they are, how they are identified and characterized, and examples of how they are used in action sports, architecture, navigation, etc. Students should know that the reflection of a line always has equal angles, that a straight line is 180° and that a right angle is 90°.

Introduction/Motivation

(Have handy a protractor and Mira ready to demonstrate to the class. Make copies of the Angles and Reflections Worksheet and have a supply of protractors for students to individually use. If available, have a Mira for each student, too, although they are not required to complete the worksheet. Be ready to share some real-world examples of how angles are used that your students will find interesting and relatable.)

All the major human-built historical masterpiece were built with great precision by following detailed design plans. Think of some famous ancient structures such as pyramids, coliseums and cathedrals. They were designed and then constructed using tools that are similar to today’s protractor, compass and Mira. These ancient tools, and others similar to them, are the early versions of the modern technology used today for designing and measuring.

While many of you are somewhat familiar with protractors, Miras and compasses, let’s talk more about what you know and do not know about these drawing tools:

• What are the purposes of these tools? (Possible answers: To design buildings, make tools, create art, lay out roads and cities, create inventions.)
• What do these tools do? (Possible answers: Measure angles, reflect objects and lines, create curved lines, arcs and circles.)
• If you have used one of these tools, which one and what have you used it to do?
• Why might engineers use these tools? (Possible answer: Before the invention of computers, these tools were used extensively to create detailed drawings and blueprints—the plans for structures, objects and other creations. These days, they are more likely to be used for quick sketches and designs.)

Writings from as early at 3100 BC in Egypt and Mesopotamia provide evidence that mathematics, and specifically geometrical techniques, were employed primarily for surveying land, constructing buildings and measuring storage containers. Later, in the 6th century BC, the Greeks formalized these early techniques into the subject we now call “geometry,” deriving the term from the Greek geo, meaning “Earth and metron, meaning “measure.”

In the beginning of the 17th century, early versions of protractors were used primarily for sea navigation and land surveying. It wasn’t until later in the 18th century that the protractor became more widely used, showing up in geometry and surveying textbooks.

(Show the class a protractor. Describe its different parts and then model how to read and use it. Remind the class that an acute angle is always the smaller number—less than 90°—and an obtuse angle [also called oblique angle] is always the larger number. Show or name some real-world and everyday examples in which protractors, and thus angles, are used, such as in sports, architecture, engineering and navigation.)

The Mira is a transparent geometry tool that reflects like a mirror. (Compare and contrast the Mira with a regular mirror while talking about the historical use of mirrors.) Before mirrors—like those we are familiar with—were commonly available, water was used for its reflective properties. Ancient mirrors made from polished obsidian have been dated to ~6000 BC. Other early mirrors were made from polished stone (Central and South America, ~2000 BC), copper (Mesopotamia, ~4000 BC) and bronze (China, ~2000 BC). During the Renaissance, mirrors were made by coating glass with metal. It was in 1835 that the modern mirror—glass coated with a thin layer of silver—was invented by German chemist Justus von Liebig. These days, aluminum is often used as the backing, instead of silver, to make mirrors that are more affordable and readily available.

(Show the class a Mira. Describe its different parts and then model how to use it.)

Many modern-day tools accomplish the same tasks as these tools that were used thousands of years ago. For example, computer-aided design software and computerized blueprints are examples of modern versions of ancient tools that performed the same functions. These modern tools provide even greater accuracy and efficiency.

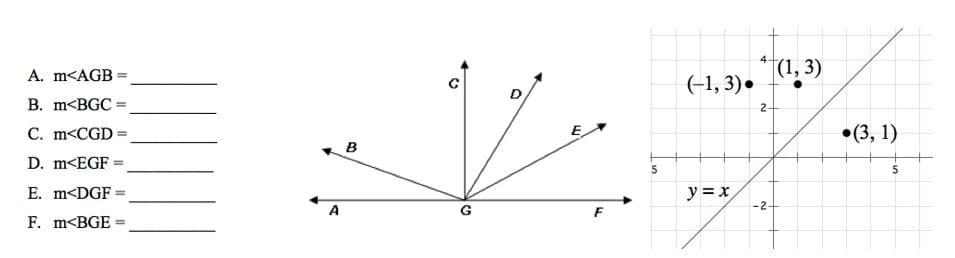
After students are introduced to the protractor and Mira, guide them through some examples, as suggested in Figure 1. Then hand out the worksheets, protractors and Miras. Following the lesson, refer to the fun and hands-on activity, Geometry Solutions: Design and Play Mini-Golf, to have students solidify their understanding.

Lesson Background and Concepts for Teachers

Lead the class through at least two examples of measuring an angle, and reflecting a point and line. See Figure 1 for some ideas of what to write on the classroom board to demonstrate and guide student practice with the tools. Demonstrating how to set up and read a protractor and a Mira correctly gives students some background knowledge on how to solve the worksheet problems.

Associated Activities

• Geometry Solutions: Design and Play Mini-Golf - Students use the tools and angle concepts learned in the lesson to first “solve the holes” for teacher-provided mini-golf course holes. Then, teams design and build their own mini-golf holes (using 2 x 4s) including their own problems and solutions for making 1-, 2- and 3-banked hole-in-one shots. They complete a worksheet to measure angles with a protractor, make angles using a protractor, and make reflections of lines with (or without) a Mira. They test to compare their on-paper predictions to real-world results using putters and golf balls.

  Watch this activity on YouTube

Vocabulary/Definitions

angle: The figure formed by two rays sharing a common endpoint (vertex). The resulting space between the two intersecting lines is often measured in degrees.

compass: A drawing tool used to create arcs and circles (given a center point). It is usually composed of two hinged parts, a spike on one end and a pencil or pen on the other.

Mira: The brand name of a plastic geometry tool (by Nasco) designed to explore and learn math concepts such as symmetry and congruence. The device is transparent yet works as a mirror to reflect points and lines drawn on paper.

protractor : A device used to measure angles.

Assessment

Pre-Lesson Assessment

Concept Evaluation: Through the discussion questions provided in the Introduction/Motivation section, determine students’ base knowledge about angles, protractors, Miras and compasses. Depending on their depth of knowledge, either explain the concepts in greater detail or move on.

Post-Introduction Assessment

Pre-Worksheet Practice Problems: Lead students through a few examples so they learn more about the tools, how to use them, and how to solve basic angle measurement and reflection problems.

Geometry Problems: Have students complete the Angles and Reflections Worksheet problems individually or in pairs. The worksheet has two sections; students use protractors in Part 1, and Miras, if available (although that tool is not required to solve the problems), in Part 2. Walk around the class to ensure students are using the tools correctly and are solving the problems.

Lesson Summary Assessment

Post-Worksheet Exploration: After the worksheets are done, have students (or pairs) share with the class how they solved certain problems, which reveals their depth of comprehension. Lead an open discussion among students, asking them to agree or disagree with the stated solution method(s) for the problem(s). Then answer their questions, correct misconceptions and demonstrate how to solve the problems.

Concluding Discussion: To wrap up the lesson, ask the class the following question. Then listen to their answers and the discussion among students to assess whether they understand the use of these tools and can connect them to their own lives. Offer prompts, as necessary.

• Today, we looked at how to use two geometric tools to solve different problems. How might engineers use these tools today? (Example answer: Architects and engineers use these tools to create the blueprints [detailed plans] for cities, buildings, factory layouts, as well as new equipment and devices, so that these structures, systems and products are constructed and manufactured into stable, efficient and reliable end results for use by people. Some artists and landscapers also use these tools to make geometric art and gardens.)

Lesson Extension Activities

Have students conduct some activities that require the use of both protractors and Miras, such as turning an image completely upside down or creating a “flower” pattern of repeated units of small/large angles.

Additional Multimedia Support

See the "Angles in Real Life" lesson for real-world examples to share with the class; see https://study.com/academy/lesson/angles-real-life-practical-applications-examples.html.

References

Copyright

Contributors

Supporting Program

Acknowledgements

This activity was developed by CU Teach Engineering, a pathway to STEM licensure through the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.