Quick Look
Grade Level: 7 (7-9)
Time Required: 1 hour
Expendable Cost/Group: US $1.00 This activity requires some non-expendable (reusable) snap cubes; see the Materials List for details.
Group Size: 2
Activity Dependency:
Subject Areas: Geometry, Problem Solving
Summary
Students learn about isometric drawings and practice sketching on triangle-dot paper the shapes they make using multiple simple cubes. They also learn how to use coded plans to envision objects and draw them on triangle-dot paper. A PowerPoint® presentation, worksheet and triangle-dot (isometric) paper printout are provided. This activity is part of a multi-activity series towards improving spatial visualization skills.
Engineering Connection
Spatial visualization is an essential skill in taking ideas that initially only exist in the mind to something that can be communicated clearly to other people and eventually turned into products, structures and systems. As such, it is an important skill for professionals within the science, technology, engineering and math (STEM) fields—particularly engineering. Engineers use spatial visualization skills whenever three-dimensional concepts, devices and ideas are being discussed. For example, chemical engineers use spatial visualization when studying three-dimensional molecules, while mechanical engineers use spatial visualization when designing prosthetic limbs that require multiple motors, gears, linkages, bearings and shafts to fit within a single assembly.
Learning Objectives
After this activity, students should be able to:
- Draw a coded plan from an object made of cubes.
- Use a coded plan to build an object made of cubes.
- Define and explain the meaning of isometric.
- Draw a shape on isometric triangle-dot paper.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Draw, construct, and describe geometrical figures and describe the relationships between them.
(Grade
7)
More Details
Do you agree with this alignment?
-
Verify experimentally the properties of rotations, reflections, and translations:
(Grade
8)
More Details
Do you agree with this alignment?
-
Apply geometric concepts in modeling situations
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Visualize relationships between two-dimensional and three-dimensional objects
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Modeling geometric figures and relationships leads to informal spatial reasoning and proof.
(Grade
7)
More Details
Do you agree with this alignment?
-
Verify experimentally the properties of rotations, reflections, and translations.
(Grade
8)
More Details
Do you agree with this alignment?
-
Objects in the real world can be modeled using geometric concepts.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Visualize relationships between two-dimensional and three-dimensional objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 10 snap cubes (interlocking cubes); a set of 100 for $10-13 at https://www.amazon.com/Learning-Resources-LER4285-Mathlink-Cubes-100/dp/B000URL296 or https://www.amazon.com/Learning-Resources-LER7584-Snap-Cubes/dp/B000G3LR9Y
- pencil with eraser, for each student
- Blank Triangle-Dot Paper, two sheets per student
- Isometric Drawing Worksheet, one per student
- (optional) computer with Internet access, to practice using the NCTM online isometric drawing tool at http://illuminations.nctm.org/Activity.aspx?id=4182
To share with the entire class:
- (optional) computer with projector to show examples as provided in the Spatial Visualization Presentation, a PowerPoint® file; alternatively, draw or print out the examples for students
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_spatviz_lesson01_activity1] to print or download.Pre-Req Knowledge
Before taking part in this spatial visualization activity, students should have taken the Spatial Visualization Practice Quiz and learned about spatial visualization in the associated lesson, Let’s Learn about Spatial Viz!
Introduction/Motivation
(Have the slide presentation up and displayed to the class, starting with slide 3.) Spatial visualization is useful for practicing engineers, has been shown to be a significant predictor of success for students in engineering, and is also a learned skill. That means we can improve our spatial visualization skills by practicing. Today, we are going develop our skills in drawing three-dimensional objects. Spatial visualization skills help you in many subjects and hobbies that require the imagination of three-dimensional shapes, such as geometry, chemistry, physics, athletics (like tennis and gymnastics) and various computer games. Practicing spatial visualization enables you to understand three-dimensional figures and representations more readily and perform better in these subjects and hobbies.
Part 1: Isometric Drawings
In the planning phase of any engineering project, an engineer needs to be able to take the vision of a new design from inside their head and illustrate it on a piece of paper or a computer screen. This process—visualizing the item as a three-dimensional object—includes the dimensions of depth, width and height. Without spatial visualization skills, engineers would be unable to envision new ideas and communicate these ideas to others.
Isometric views are useful for displaying three-dimensional objects on a two-dimensional piece of paper. More specifically, we use triangle-dot paper to draw objects isometrically. (Display slide 4, which is the same as Figure 1.) This image shows a 3-D cube depicted in two different ways. On the left, the cube is drawn non-isometrically in that the angles in the corners are not equal and the sides each have different areas. However, on the right, the cube is drawn such that the sides of the cube connect at a “corner,” making equal angles of 120°. We call this an isometric view of the cube. Also notice that in the illustration on the right, all the sides of the cube are the same size. During this activity, we are going to practice drawing shapes isometrically. (Slide 5, same as Figure 4, shows a house depicted isometrically using AutoCAD.)
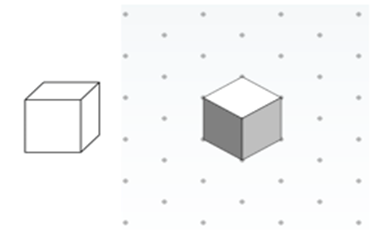
Part 2: Coded Plans
Next, we are going to learn about coded plans. Before explaining coded plans, let’s do an activity that demonstrates the importance of using coded plans. First, team up with a person next to you.
(Direct the class through the following exercise: Have partner #1 close their eyes. Show all partner #2 students the left image in slide 6, which is the same as Figure 2. Inform partner #1 to keep their eyes closed while partner #2 describes the image. Let the object description continue for a couple of minutes. When finished, have partner #1 draw the object as accurately as possible.)
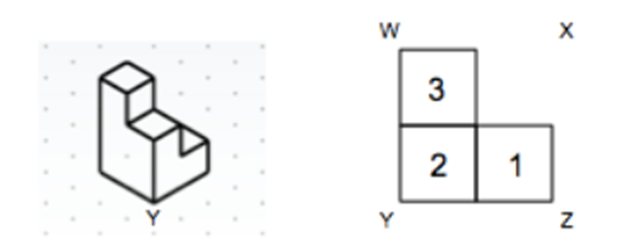
For such a simple-appearing object, that was pretty challenging, right? Perhaps you described the object using phrases like these:
- It is made of six cubes.
- Three cubes are stacked, one on top of the other. Next to that are two cubes, also stacked one on top of the other. Next to that stack is one single cube.
Even with this explanation, it is possible that your partner incorrectly envisioned the object. Imagine if you were an engineer who needed to design a much more complicated object than the one you tried to describe—it would be even more difficult! This is precisely why we use coded plans in engineering drawings. Coded plans are a type of tool used by engineers to express three-dimensional objects on two-dimensional surfaces. A coded plan defines the shape of a structure or object composed of blocks. (Click to reveal the right side of slide 6, which is the same as the right side of Figure 2—a coded plan of the same image just described and drawn by students.) For instance, a coded plan is shown here. Notice that the corners of the object are labeled by letters. Notice also that the numbers inside the squares represent the number of cubes that are stacked on top of each other. Next, we will do some activities to practice making coded plans and isometric drawings.
Procedure
Background
The term “isometric” literally means “equal measure.” In other words, when we isometrically draw an object composed of multiple cubes, the cube faces are all the same area and the corner angles are all equal and 120°. Triangle-dot paper is useful because the dots are situated 120° from each other, which facilitates drawing 3-D objects. For students just starting to practice spatial visualization, it is beneficial to use toy blocks with the ability to interlock and form larger shapes composed of the cubes (such as the recommended “snap cubes” in the Materials List; see Figure 3.)

Engineers use computer-aided drafting software programs such as AutoCAD® to create blueprints and design plans. Figure 4 (also on slide 5) shows a house that was depicted isometrically using AutoCAD.
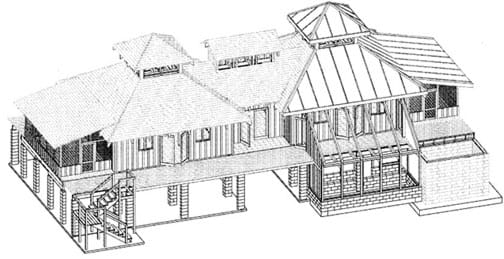
Before the Activity
- Gather materials and make copies of the Blank Triangle-Dot Paper and Isometric Drawing Worksheet.
- (optional) Decide if you want to incorporate having students practice with the NCTM online isometric drawing tool that enables them to draw their own isometric objects and rotate the objects around the x-, y- and z-planes.) If so, arrange for and set up computer and Internet access to do so.
- Prepare to project the Spatial Visualization Presentation, a PowerPoint® file, and use its content to aid in your instruction, as makes sense for your class. Slides 3-11 support this activity. The slides are animated so a mouse or keyboard click brings up the next graphic or text.
With the Students: Introduction
- Present to the class the Introduction/Motivation content, supported by slides 3-6. Also ask the pre-assessment question, as described in the Assessment section.
- Divide the class into groups of two students each.
- Hand out two pieces of triangle dot paper to each student and 10 cubes to each pair. Explain that students are to share their interlocking cubes with their partners, primarily work independently on their drawings, but feel free to share their drawings and troubleshoot with their partners. Instruct students to work on one piece of triangle-dot paper until it is full.
Part 1. Basics of Drawing Cubes on Triangle-Dot Paper
- As a class, direct students to each put one cube on the desk in front of themselves. Ask the students to draw their cubes on isometric paper (individually). To begin with, direct them to move sequentially through the drawing using the following steps. (As makes sense, also show the drawing tips on slide 7.)
- Draw a dot representing a corner of the cube.
- Draw lines that represent the edges of the cube that connect to that corner.
- Draw a single surface of the cube.
- Complete all other surfaces of the cube.
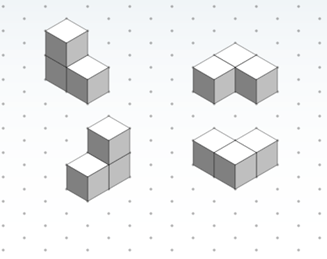
- Once finished, have students share their drawings with their partners. Expect the drawings to resemble the left-most image in slide 8 (same as Figure 5-far left; click the mouse/keyboard to reveal it).
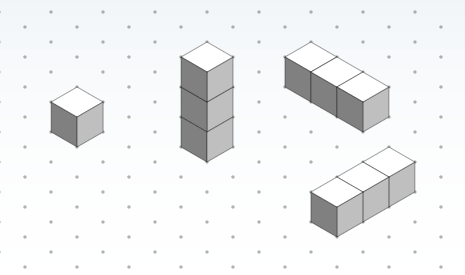
Figure 5. Various cube shapes drawn on triangle-dot paper. -
Have students stack two blocks on top of the original block to form a three-cube “tower.” Ask them to draw the stacked cubes on isometric paper and then share with their partners. Expect their drawings to resemble the center image in slide 8 (same as Figure 5-center; click the mouse/keyboard to reveal it).
-
Finally, have students turn their towers on their sides so that three cubes are touching the desk/table surface. Now, ask the students to draw the stacked tower at this angle on isometric paper. Expect their drawings to resemble one of the two images on the right side of slide 8 (same as Figure 5-far right; click the mouse/keyboard to reveal it), depending on which way they oriented the object.
-
At this point, stop and make sure that all students are getting the hang of drawing on isometric triangle-dot paper. If students are struggling, spend more time on the first three steps. If necessary, display the answers for the class and/or demonstrate how to draw each of the three images. Notice how the faces in between the cubes and the backside/bottom of each cube are not drawn directly; we know that those sides are part of the cubes, but the isometric drawing cannot depict all details of a 3-D object.
Part 2. Drawing Shapes of Increased Complexity on Triangle-Dot Paper
- Direct the students to each use four blocks to make a shape of their choosing.
- Ask the students to individually draw the shapes of their objects on isometric paper.
- Have partners switch objects and draw the shape of their partners’ objects.
- Once both partners are finished drawing the objects they created, as well as the objects created by their partners, have them cross-check their drawings to make sure that they are correct.
- Have students repeat the four previous steps, adding one more block to their shapes for each iteration. Permit students to continue working for about five minutes. If they are working through these steps quickly, see the Extension Activities section for ways to challenge them further.
- Assign students to complete the worksheet. Observe and assist as necessary.
(optional) Part 3. Drawing Isometric Views from Coded Plans
As an optional/extra credit assignment, present to students the following peer teach exercise:
- Still in pairs, show students the drawing tips on slide 9.
- Then show students the coded plan shown to the far left on slide 10 (same as Figure 6-far left. Ask them to draw two different isometric views of the coded plan. It may be necessary to rotate a sample cube shape to help students to understand this challenge. Click on slide 10 to reveal the solutions to the four possible isometric views.
- Once each student has drawn two isometric views, have student pairs explain to each other how they produced their drawings.
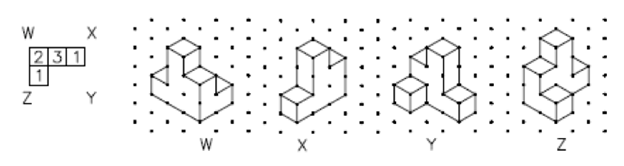
Vocabulary/Definitions
coded plan: A spatial visualization term that refers to a method of describing a three-dimensional shape two-dimensionally.
isometric: Of or having equal dimensions. The isometric view of an object is the angle at which an equal angle (120°) exists between all axes (such as looking down a corner of the object).
spatial visualization: The ability to mentally manipulate two- and three-dimensional objects. It is typically measured with cognitive tests and is a predictor of success in STEM fields. Also referred to as visual-spatial ability.
triangle-dot paper: A grid of dots arranged equidistant from one another. Used in making isometric sketches. Also called isometric paper.
Assessment
Pre-Activity Assessment
Question/Answer: Ask students: Why are isometric drawings important to engineers? (Point to make: Isometric drawings represent three-dimensional objects on a two-dimensional surface. By doing this, engineers can depict complicated 3-D objects in a way that is easy to share and describe. Without isometric drawings, engineers would require 3-D models of each idea/concept, which would be costly, cumbersome and inconvenient.)
Activity Embedded Assessment
Worksheet: After completing the classroom instruction on isometric drawing, assign students to complete the Isometric Drawing Worksheet. Observe whether students are able to draw the rotated objects or if they are struggling. Assist them if necessary. Review their answers to gauge their depth of understanding.
Post-Activity Assessment
Discussion: Ask students to explain and describe their drawings with specific focus on the isometric concept. What strategies did they use to draw their cube shapes? What were the limitations they experienced, if any? How did students solve any drawing challenges? Since everyone has worked through the same exercises, group sharing of their challenges and approaches informs the teacher of students’ depth of understanding and provides their peers with relevant ideas and tips.
Activity Extensions
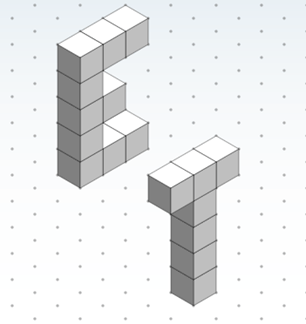
- Have students rotate one of their snap block objects to see how many new angles they can draw it from. Show slide 11 (same as Figure 7) as an example.
- Have students rotate a shape in their minds and draw it on triangle-dot paper without physically rotating any cubes/shapes.
- Have each partner use four cubes to make a shape and place the object under their partners’ chairs without showing the shape. Then, have students reach under their chairs and feel the objects (without looking at them) and draw the shapes they felt. Once finished, have them compare their drawings to the objects.
- Have students draw the capital letters E and T in isometric view; show slide 11 as an example (same as Figure 8).
- Ask students to calculate the volume and surface area of one of the shapes they drew. To help with the challenge, tell them that the length of one side of a cube is 5 cm.
Activity Scaling
- For lower grades, guide students through drawing the cube shapes by using an overhead projector. Depending on how much guidance is needed, repeat Part 1 for other very simple shapes.
- For higher grades, challenge students to conduct all the Activity Extensions.
Additional Multimedia Support
Have students practice with the NCTM online isometric drawing tool to draw isometric objects and rotate the objects around the X, Y and Z planes: http://illuminations.nctm.org/Activity.aspx?id=4182.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn how to create two-dimensional representations of three-dimensional objects by utilizing orthographic projection techniques. They build shapes using cube blocks and then draw orthographic and isometric views of those shapes—which are the side views, such as top, front, right—with no de...

In this lesson, students are introduced to the concept of spatial visualization and measure their spatial visualization skills by taking the provided 12-question quiz. Following the lesson, students complete the four associated spatial visualization activities and then re-take the quiz to see how mu...

Students learn about one-axis rotations, and specifically how to rotate objects both physically and mentally to understand the concept. They practice drawing one-axis rotations through a group exercise using cube blocks to create shapes and then drawing those shapes from various x-, y- and z-axis ro...

Students learn about two-axis rotations, and specifically how to rotate objects both physically and mentally about two axes. Students practice drawing two-axis rotations through an exercise using simple cube blocks to create shapes, and then drawing on triangle-dot paper the shapes from various x-, ...
Copyright
© 2011 by Regents of the University of ColoradoContributors
Emily C. Gill; Jacob Segil; Emily BreidtSupporting Program
Engineering Plus Degree Program, University of Colorado BoulderAcknowledgements
This activity was developed by the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.
This lesson plan and its associated activities were derived from a summer workshop taught by Jacob Segil for undergraduate engineers at the University of Colorado Boulder. The activities have been adapted to suit the skill level of middle school students, with suggestions on how to adapt activities to elementary or, in some instances, high school level.
Last modified: October 21, 2020









User Comments & Tips