Quick Look
Grade Level: 7 (7-9)
Time Required: 1 hour
Expendable Cost/Group: US $1.20
Group Size: 2
Activity Dependency:
Subject Areas: Geometry, Problem Solving

Summary
Students learn about two-axis rotations, and specifically how to rotate objects both physically and mentally about two axes. A two-axis rotation is a rotation of an object about a combination of x, y or z-axes, as opposed to a single-axis rotation, which is about a single x, y or z-axis. Students practice drawing two-axis rotations through an exercise using simple cube blocks to create shapes, and then drawing on triangle-dot paper the shapes from various x-, y- and z-axis rotation perspectives. They use the right-hand rule to explore the rotations of objects. A worksheet is provided. This activity is part of a multi-activity series towards improving spatial visualization skills. At activity end, students re-take the 12-question quiz they took in the associated lesson (before conducting four associated activities) to measure how their spatial visualizations skills improved.Engineering Connection
Rotating objects is a spatial visualization technique that enables engineers to visualize complicated assemblies in mechanisms and other systems in a fields such as physics, chemistry, mathematics and engineering. Spatial visualization is an essential and learnable skill that engineers use to clearly communicate their ideas to other people so the ideas can ultimately be turned into real-world products, structures and systems.
Many engineering applications require the depiction of objects from multiple viewpoints, such as mechanical drawings used to manufacture components, architectural drawings, and depictions of chemical compounds. In order to produce these views, an object must be rotated across multiple axes, called two-axis rotations. This skill is similar to lifting up an object and looking at it from all sides, which is not always possible since some objects/components may be too large, heavy or inaccessible for physical manipulation. Instead, engineers must be able to visualize what various viewpoints look like without physically manipulating objects. Typically, engineers use computer-aided design (CAD) software to help visualize complicated rotations of objects. This activity helps students develop two-axis rotation skills.
Learning Objectives
After this activity, students should be able to:
- Rotate objects about two axes.
- Translate the rotation of one block to a second block.
- Use the right-hand rule to explore rotations of objects.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Draw, construct, and describe geometrical figures and describe the relationships between them.
(Grade
7)
More Details
Do you agree with this alignment?
-
Apply geometric concepts in modeling situations
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Visualize relationships between two-dimensional and three-dimensional objects
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Modeling geometric figures and relationships leads to informal spatial reasoning and proof.
(Grade
7)
More Details
Do you agree with this alignment?
-
Objects in the real world can be modeled using geometric concepts.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Visualize relationships between two-dimensional and three-dimensional objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 8 snap cubes (interlocking cubes); a set of 100 at https://www.amazon.com/Learning-Resources-LER4285-Mathlink-Cubes-100/dp/B000URL296 or https://www.amazon.com/Learning-Resources-LER7584-Snap-Cubes/dp/B000G3LR9Y
- pencil with eraser, for each student
- Blank Triangle-Dot Paper, two sheets per student
- Rotations Practice Worksheet, one per student
- Spatial Visualization Practice Quiz, one per student
To share with the entire class:
- (optional) computer and projector to show examples as provided in the Spatial Visualization Rotations Presentation, a PowerPoint® file; alternatively, draw the examples for students

Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_spatviz_lesson01_activity4] to print or download.Pre-Req Knowledge
Before taking part in this spatial visualization activity, students should have taken the Spatial Visualization Practice Quiz and learned about spatial visualization in the associated lesson, Let’s Learn about Spatial Viz! They should know about isometric drawing, how to use triangle-dot paper and coded plans (as can be learned in the associated activity, Connect the Dots: Isometric Drawing and Coded Plans), orthographic views (as can be learned in the associated activity, Seeing All Sides: Orthographic Views), and have been introduced to rotations (as can be learned in the associated activity, Let’s Take a Spin: One-Axis Rotations).
Introduction/Motivation
(Have the slide presentation up and displayed to the class, starting with slide 26.) Today we are going to explore rotations about two axes. You experience two-axis rotations throughout your everyday lives. How many times do you rotate a USB stick before getting it to correctly insert into a computer? How many different ways can you put on a t-shirt? But first, let’s quickly review one-axis rotations. Objects can be rotated about the three axes: x, y and z and any combination of the three.
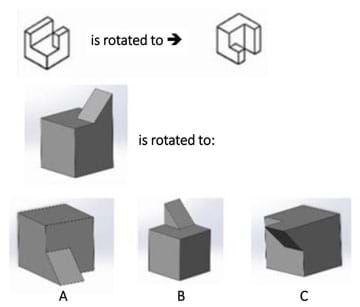
(Show students slide 27; same as Figure 1.) Do you see that the first block on the top left is the same block as on the top right? We are simply looking at it from another angle. How would you describe this rotation? Take a look at this figure and determine what you think the answer is. Now explain to a partner what you think is the correct answer and why. What are some methods you used to determine how the block was rotated? How would you define the rotation in terms of a positive or negative rotation about the x, y and/or z axes? (Answer: Negative rotation about the y-axis, negative rotation about the z-axis.)
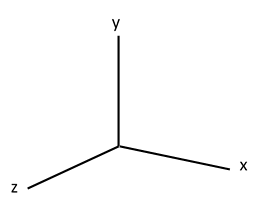
Now, let’s do a quick recap of the right-hand rule (refer to slide 24 as a review from the previous associated activity). It works as follows: point your thumb parallel to the axis you are rotating about and curve your fingers naturally towards the palm of your hand. Your fingers will move in the same way that the object will move. The axes shown in slide 23 (same as Figure 2) are the positive axes, and if you flip each axis 180°, you get the negative axes.
Procedure
Before the Activity
- Gather materials and make copies of the Blank Triangle-Dot Paper, Rotations Practice Worksheet and Spatial Visualization Practice Quiz.
- Prepare to project the Spatial Visualization Presentation, a PowerPoint® file, and use its content to aid in your instruction, as makes sense for your class. Slides 26-29 support this activity, with review slides 23-24 from the previous associated activity. The slides are animated so a mouse or keyboard click brings up the next image, text or slide.
With the Students
- Present to the class the Introduction/Motivation content. Also ask the pre-assessment question, as described in the Assessment section.
- Hand out to each student the cubes and triangle-dot paper.
- Have each student build a three-block-long rectangular object.
- Have students draw the Cartesian coordinate system on triangle-dot paper.
- Direct students to draw the object before and after a positive x rotation followed by a positive y rotation. (Expect each student to finish with three consecutive drawings. As necessary, show students slides 27-29 and their tips: Use the right-hand rule; clockwise = negative rotation; counter-clockwise = positive rotation; two-axis rotation is not commutative [order matters!], and the “write a rule” approach to take note of their own logic and methods.)
- Share and compare students’ drawings with the class.
- Divide the class into student pairs.
- Have students complete the Block-n-Swap Relay as follows:
- Have students sit with their partners.
- Have each student use the cubes to build an object and then proceed to define a rotation about two axes.
- Have each student draw the original isometric view of the object and then draw the object after the defined rotation.
- After a few minutes, have students pass each object and defined rotation to their partners.
- Then the partners draw the rotated views of the objects.
- Have partners compare the isometric drawings with each other.
- Discuss as a class, as described in the Assessment section.
- Assign students to complete the worksheet. Observe and assist as necessary.
- Re-administer the Spatial Visualization Practice Quiz, as described in the Assessment section.
Vocabulary/Definitions
right-hand rule : A useful memory tool in the rotation of objects that uses a person’s right hand and fingers to help in understanding orientation conventions for vectors in three dimensions. Often used in physics and math.
spatial visualization: The ability to mentally manipulate two- and three-dimensional objects. It is typically measured with cognitive tests and is a predictor of success in STEM fields. Also referred to as visual-spatial ability.
triangle-dot paper: A grid of dots arranged equidistant from one another. Used in making isometric sketches. Also called isometric paper.
Assessment
Pre-Activity Assessment
Question/Answer: Ask students: Why are two-axis rotations are important to engineers? Why would a biomedical engineers designing a new heart valve need to see it from different views? Why is it important to see these different views? (Point to make: Our 3-D world is difficult to represent on 2-D screens and paper. The ability to rotate an object around in one’s mind helps complex, real-life challenges be understood more clearly. It is important for engineers to be able to visualize 3-D objects in order to make design decisions that will work effectively in the 3-D world in which our designs, products and inventions must operate.)
Activity Embedded Assessment
Block-n-Swap: During the Block-n-Swap Relay, observe students to make sure they are able to draw the rotated objects. If they are struggling, assist them as necessary.
Worksheet: After students complete the Block-n-Swap Relay exercise, assign them to complete the Rotations Practice Worksheet. Observe whether students are able to draw the rotated objects or if they are struggling. Assist them as necessary. Review their answers to gauge their depth of understanding.
Post-Activity Assessment
Discussion: Ask students to explain and describe their drawings with specific focus on two-axis rotational views. What strategies did they use to draw their cube shapes? What were the limitations they experienced, if any? How did students solve any drawing challenges? Since everyone has worked through the same exercises, group sharing of their challenges and approaches informs the teacher of students’ depth of understanding and provides their peers with relevant ideas and tips.
Spatial Visualization Post-Quiz: To conclude the series of four spatial visualization practice activities, re-administer the Spatial Visualization Practice Quiz, which students took as a pre-assessment during the associated lesson. Now that they have practiced their spatial visualization skills throughout four activities, show them how much they have improved! A “passing score” is any score over eight points (out of 12 possible). However, it is most important to emphasize individual student improvement gains.
Activity Extensions
To further challenge students, direct them to draw the rotation views of various objects without looking at the blocks.
Activity Scaling
- For lower grades, provide students with a longer time on the Block-n-Swap Relay. Also, spend more time introducing the concept by having the entire class make the same object, define a rotation and draw the rotation isometrically. Then, go over the correct answer with students. This provides less-advanced students with more time to fully practice and grasp the topic before branching off in pairs.
- For higher grades, have students use more blocks to make more complicated objects, and during the Block-n-Swap Relay, do not permit students to use the blocks to visually aid in their rotation drawings. Adjust the time allotment as needed.
Additional Multimedia Support
As an additional or alternative test, you may want to purchase for $25 a license to use a scanned digital version of the Purdue Spatial Visualization Test: Rotations from Educational Testing Service at https://www.spatiallearning.org/tools/revised-purdue-spatial-visualization-test-revised-psvtr-visualization-of-rotations.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn about one-axis rotations, and specifically how to rotate objects both physically and mentally to understand the concept. They practice drawing one-axis rotations through a group exercise using cube blocks to create shapes and then drawing those shapes from various x-, y- and z-axis ro...

In this lesson, students are introduced to the concept of spatial visualization and measure their spatial visualization skills by taking the provided 12-question quiz. Following the lesson, students complete the four associated spatial visualization activities and then re-take the quiz to see how mu...

Students learn about isometric drawings and practice sketching on triangle-dot paper the shapes they make using multiple simple cubes. They also learn how to use coded plans to envision objects and draw them on triangle-dot paper.

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...
Copyright
© 2011 by Regents of the University of ColoradoContributors
Emily C. Gill; Jacob Segil; Emily BreidtSupporting Program
Engineering Plus Degree Program, University of Colorado BoulderAcknowledgements
This activity was developed by the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.
This lesson plan and its associated activities were derived from a summer workshop taught by Jacob Segil for undergraduate engineers at the University of Colorado Boulder. The activities have been adapted to suit the skill level of middle school students, with suggestions on how to adapt activities to elementary or, in some instances, high school level.
Last modified: August 8, 2025









User Comments & Tips