Quick Look
Grade Level: 7 (6-8)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 Requires the use of non-expendable (reusable) LEGO® MINDSTORMS® kits with sensors and other supplies, estimated at $428 per group; see the Materials List for details.
Group Size: 4
Activity Dependency: None
Subject Areas: Measurement, Physics
NGSS Performance Expectations:

| MS-ETS1-4 |

Summary
Students measure different types of small-sized beams and calculate their respective moments of inertia. They compare the calculations to how much the beams bend when loads are placed on them, gaining insight into the ideal geometry and material for load-bearing beams.Engineering Connection
Civil and mechanical engineers design structures for buildings and machines to make sure that the structures hold up under the various loading conditions that they are expected to encounter. Engineers use different types of materials and designs to achieve durable structures. Beam stiffness is essential to consider, which entails an understanding of beam material and geometry. Thus, the measurement and testing of beams, similar to students' explorations in this activity, is very important to successful structure design.
Learning Objectives
After this activity, students should be able to:
- Define a beam.
- Describe beam shapes and materials that should be used for various structures.
- Explain how a beam's area moment of inertia relates to the amount of deflection that the beam allows.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ETS1-4. Develop a model to generate data for iterative testing and modification of a proposed object, tool, or process such that an optimal design can be achieved. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop a model to generate data to test ideas about designed systems, including those representing inputs and outputs. Alignment agreement: | Models of all kinds are important for testing solutions. Alignment agreement: The iterative process of testing the most promising solutions and modifying what is proposed on the basis of the test results leads to greater refinement and ultimately to an optimal solution.Alignment agreement: | |
Common Core State Standards - Math
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
(Grade
7)
More Details
Do you agree with this alignment?
-
Describe qualitatively the functional relationship between two quantities by analyzing a graph (e.g., where the function is increasing or decreasing, linear or nonlinear). Sketch a graph that exhibits the qualitative features of a function that has been described verbally.
(Grade
8)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
The selection of designs for structures is based on factors such as building laws and codes, style, convenience, cost, climate, and function.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
(Grade
7)
More Details
Do you agree with this alignment?
-
Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
(Grade
7)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
-
Describe qualitatively the functional relationship between two quantities by analyzing a graph (e.g., where the function is increasing or decreasing, linear or nonlinear). Sketch a graph that exhibits the qualitative features of a function that has been described verbally.
(Grade
8)
More Details
Do you agree with this alignment?
New York - Science
-
Develop a model to generate data for iterative testing and modification of a proposed object, tool, or process such that an optimal design can be achieved.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
- LEGO EV3 Intelligent Brick available at https://www.amazon.com/LEGO-Mindstorms-EV3-Intelligent-Brick/dp/B00G1L0278
- various rectangular model beams, at least 2 feet long and 1/2 in thick:
- 3 (or more) wooden beams with square cross-sections, one slightly larger than the others
- 1 metal beam (steel or aluminum) with a square cross-section, same size as one of the wooden beams
- 1 cardboard sheet or stiff stationery to fold and create a basket of 4 in × 2 in × 2 in (10.16 cm x 5.08 cm x 5.08 cm) dimensions (Note: The cardboard sheet can be of any size; the dimensions of the basket are what matters.)
- 9 - 18 AA batteries, or small weights (Note: AA batteries for the basket are preferable; however, AAA batteries or any type of weight can be used, as long as the beam deflection is noticeable enough to be read by the ultrasonic sensor.)
- 2 clamps
- 1 ruler or caliper
- tape, scotch or any cellophane type (amount depends on user preference as long as hanging platform is above the EV3 sensor)
- Test-a-Beam Graphing Worksheet, one per student
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set and the Intelligent Brick
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_beam_activity1] to print or download.Pre-Req Knowledge
A familiarity with basic geometrical shapes, decimals, area calculation, displacement concepts and graphing.
Introduction/Motivation
Imagine that you are exploring a city, and you notice many building construction sites. At one site, you see many people wearing hard hats, carrying materials and big machines; they are all working to build a skyscraper. At the moment, it doesn't look like much of a building, but you see what looks like huge, long metal "sticks" that are somehow being put together (Draw a building frame on the board or show a photograph of a building being framed up.) You may not realize it at that moment, but those "sticks" are really important when it comes to making sure the building stands up and stays up.
Those long "sticks" are referred to as beams (Draw a beam on the board with dimensions.) A beam, by definition, is a long structure whose length is several times longer than any of its cross-sectional dimensions.
Beams can be made of many different shapes and sizes, as well as different materials, such as wood, metals, and in some machines, even plastics.
Depending on what is being built, engineers choose to use certain kinds of materials with specified sizes, all of which can affect the stiffness of the beam, since the beam will undergo a certain amount of deflection when weight is placed on it.
But how do engineers know what size and/or what materials are best to use for each situation? How do structural engineers know that what they design and create will not move too much when a load (weight) is put on it? That question is what we are going to investigate today.
Procedure
Before the Activity
- Gather materials and make copies of the worksheet.
- Set up group stations with at least two clamps at each.
- Make a cardboard basket for each station, or have students cut out and make the baskets.
- Set up a deflection measurement device using an ultrasonic sensor along with the EV3 brick.
- Use the same amount of weight for each station, using batteries or experimental weights.
- For each station, use tape to place the cardboard basket on one of the beams, attached at the very tip.
- Divide the class into groups of four students each.
- Present the following information to students:
To get a sense of how rigid a beam is and what can influence its rigidity, let's consider a flexible plastic ruler. If you bend it when it is flat, it becomes easier to bend. However, if you turn it on its edge and bend it, then it doesn't bend much. Notice that the ruler has the same cross-sectional area in both cases. So if it is not area that affects the ruler's rigidity, then what could it be?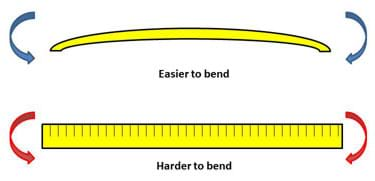
Just by turning the ruler and bending it along its edge, we increased the ruler's area moment of inertia. It might seem like a complicated term, but all it means is that because of the ruler's cross-sectional shape and dimensions, the bendability of the ruler can change when you bend it in a different direction (or orientation). To calculate the area moment of inertia (I) of a square cross-section, we use the equation below: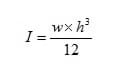
The letters w and h represent the width and the height of the beam, respectively. As a first example, let's say the ruler you bent has a rectangular cross section. If its width was 0.1 inches and its height was 1 inch, then the calculation would be carried out as follows: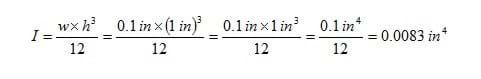
But, if you flipped the ruler on its side, then its width would be its height, and vice versa. The calculation would be shown as follows: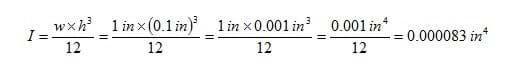
Just because you flipped the ruler, you can bend it easier, since the area moment of inertia is less in that orientation. Now, how about we try bending beams of our own?
For this activity, we have wooden beams of different sizes, and we are going to measure the width and height of their cross-section. This is important, because you will use these measurements to calculate the area moment of inertia of the beam. We are also going to tape a platform at the tip of each beam and hang a certain amount of weight on the platform. We are also going to put the same amount of weight on the tips of each of those beams, and measure how much the tip moves by using a LEGO EV3 set-up with a sensor. Then you can draw a graph of area moment of inertia vs. deflection, and see what you get. Once you are done with that, you can take a metal beam and take a wooden beam of the same cross-section, and repeat what was done with the wooden beams before. Let's see what conclusions you can come up with when it comes to beam size and material type!
With the Students
Part 1: Using wooden beams only:
- Have each student clamp the wooden beam in place at its table, with 2 feet of beam length overhanging from the tabletop. Place one clamp on the back end of the beam touching the table, and the other clamp where the beam starts to hang over the table. Refer to Figures 1 and 2 for the set-up.

Figure 1. Beam with load. - Have students turn on the EV3 and record the initial position of the basket on the beam. This is done by using the "View" option in the EV3 and selecting "Ultrasonic Sensor – cm" to view readings of the ultrasonic sensor. To start distance measurements, select the port that the sensor is connected.

Figure 2. Place the weighted basket directly above the ultrasonic sensor. - Have students place weight (AA batteries or small weights) in the basket and record the position of the basket after the weight is placed. Keep track of the amount of batteries used to weigh down the beam; then use the same amount of weight for all beams tested.
- Have students calculate the displacement for each differently-sized beam. Also, have them use the ruler or caliper to calculate the area moment of inertia of each beam.
- Using the obtained (and calculated) data, have students create graphs of area moment of inertia (y-axis) vs. deflection (x-axis) for the set of beams on the Test-a-Beam Graphing Worksheet. Each beam will deflect a certain amount under a constant weight.
- Ask students for interpretation: What do they think the graph tells us about the beams tested?
Part 2: Using wooden and steel beams of same cross-section:
- Repeat steps 1-5 above.
- Have students compare deflection and area moment of inertia values for the wood and steel beams. Are they different? How and why?
Vocabulary/Definitions
area moment of inertia: Value that depends on cross-sectional shape and dimensions, which tells how much a beam will resist bending. (Square Cross-Section: I=bh^3/12; Circular Cross-Section: I=(pi)d^4/64)
beam: A basic structure whose length is several times larger than its cross-sectional dimensions.
deflection: Change in position of a point along a structure. (Fixed End Beams With End Load: y=FL^3/(EI) where y equals distance deflected, F is force on beam, L is length of beam up to fixed portion, E is elastic modulus, and I is moment of inertia)
sensor: A device that measures or "senses" a specific quantity (temperature, distance, level of light/darkness).
stiffness: A material or structure's resistance to change of shape.
Assessment
Pre-Activity Assessment
What Can I Bend Easily? As a warm-up to the activity, have students find ordinary, everyday, pliable and safe objects from around the classroom and notice the size, shape, and material of each (examples: eraser, pencil, ruler, book). Have each student slightly bend an object in one orientation, and then bend it sideways. Ask students what they notice, especially if the object is not shaped the same on all sides. (Answer can be found under question 1 in Test-a-Beam Assessment Sample Answers)
Activity Embedded Assessment
What Happens When...? Evaluate students on two criteria: conducting experimental measurements and the interpretation of graphical data. When conducting experimental measurements, expect groups to have similar displacement results, given that the same-size beams are being used. When interpreting data, expect students to be able to interpret what is seen on a graph that is plotted from their own obtained results. This opens the way to them having more insight into engineering design in terms of structures. What happens when the area moment of inertia increases? What happens when a metal is used to hold weight instead of wood? (Answer can be found under question 2 in Test-a-Beam Assessment Sample Answers)
Post-Activity Assessment
Discussion: Discuss how beams are designed today, and in what new structures they may be used. What beam shapes have you seen? What do they look like? Why do you think the cross section of modern beams look the way they do (particularly the typical I-beam section)? What beam shape and material would you use for a house? What would you use for a large building? Why? (Answer can be found under question 3 in Test-a-Beam Assessment Sample Answers)
Safety Issues
- Slowly load and unload the weights to ensure beams do not flail out and hit anyone.
Troubleshooting Tips
- To improve accuracy when taking displacement measurements, make sure that the hanging weight is absolutely still.
- If the ultrasonic sensor is not sensitive enough to detect small differences in deflection, try measurement using the centimeter scale, and/or increasing the overhang length of the beam.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!Copyright
© 2013 by Regents of the University of Colorado; original © 2010 Polytechnic Institute of New York UniversityContributors
Ronald PovedaSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed under the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.
Additional support was provided by the Central Brooklyn STEM Initiative (CBSI), funded by six philanthropic organizations.
Last modified: May 17, 2023





User Comments & Tips