Hands-on Activity Designing an Elliptical Pool Table

Learning Objectives

After this activity, students should be able to:

• Use the equation of an ellipse to calculate the various properties of an ellipse.
• Design an elliptical pool table that ensures players can always make the shot.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• access to an assortment of building materials from which to make an elliptical pool table
• 1 marker, to mark the ellipse foci
• circular wooden dowels, 1-1.5 inch diameter, to serve as cue sticks to hit the balls
• 2-4 small balls such as golf balls, pool balls or table tennis balls; golf balls are often ideal
• access to a computer with Internet access, to do online research

To share with the entire class:

• an assortment of building materials from which groups choose (as their hypothetical budgets permit) to make their elliptical pool tables; suggested materials for the table surface/base: wood, strong cardboard; suggested materials for the table border: wood, cardboard, rubber bands, chopsticks, (foam swimming) pool noodles or other materials requested by groups (as the teacher permits)
• felt, enough for each group to have a piece to cover its table, which could be 1 x 2 feet minimum to 2 x 2 feet maximum
• an assortment of tools such as scissors, markers, tape, hot glue gun and glue sticks
• computer with Internet connection and projector to show the class an online video clip and the Ellipses Presentation, a PowerPoint® file

For the (optional) drawing exercise (see slide 5), each student needs:

• graph paper and pencil
• 2 push pins
• string

Worksheets and Attachments

Introduction/Motivation

Imagine you are traveling with your family and end up in an elliptical-shaped room. You are standing next to and talking to a family member. During the conversation, you get distracted by something at the other end of the room and begin to walk away. While walking away, your family member’s voice becomes fainter until s/he can no longer be heard. Then, at a certain point in the room, you can hear your family member perfectly clear again! Then, if you move away from that location, you can no longer hear the family member.

What is going on? (Give students two minutes to discuss with their neighbors their ideas that explain this phenomenon. Then, for three to five minutes, have students share their explanations for how and why this could be possible. Then provide students with the explanation.)

In some buildings, you can experience this phenomenon, which is caused by the unique design of the elliptical structure. An ellipse has the property that if light or sound waves emanate from one focus, they are reflected to the other focus. Take a look at this example of a whispering gallery in the U.S. Capitol building in Washington, DC. (Play the 1:13-minute video at https://www.youtube.com/watch?v=FX6rUU_74kk.) 

(Next, show students the PowerPoint® presentation to cover the math and characteristics that define ellipses [slides 1-4]. If time permits, have students draw ellipses using pencils, graph paper, push pins and string [slide 5]. Then introduce the engineering design project for this activity with the text below, including a diagram that shows the steps of the engineering design process [slide 7] and a listing of the design constraints [slide 8]. Walk students through the engineering design process with an emphasis on planning and redesign. Slides 9-11 provide photographs of student example projects—for the teacher.)

During today’s activity, we are going to explore the different characteristics and properties of ellipses.

• A focus is one of two points that define the shape and size of an ellipse.
• If light or sound waves emanate from one focus of an ellipse, they are reflected to the other focus.
• People have used this ellipse property to create whispering galleries, which are structures that allow someone who is whispering in one area to be heard clearly by someone in another area, but not by anyone else.

In today’s project, you will apply what you have learned to create an elliptical pool table and follow the steps of the engineering design process to guide you. This is your engineering design challenge: Your client says the game of pool has become too mundane and is too simple. As engineers, you are challenged to create an elliptical pool table with one pocket, in which one focal point is the pocket and the other focal point is the break spot. The table must be at least 1 x 2 feet and no larger than 2 x 2 feet and each team has a $10 budget.

Procedure

Before the Activity

• Gather an assortment of building materials and tools.
• Decide on the team budget (such as $10 per group) and assign dollar values to the building materials. For example, $3 for a pool noodle, $2 for felt, $1 for 20 rubber bands, $1 for two sets of chopsticks. You may want to vary the budget, depending on the available materials or other considerations.
• Be ready to show the class the eight-slide Ellipses Presentation, a PowerPoint® file. For the teacher’s reference, slides 9-11 show photographs of some example student-created pool tables.

With the Students

1. Administer the pre-activity math problem, as described in the Assessment section.
2. Present to the class the Introduction/Motivation content, which includes playing a quick online video of a whispering gallery and then showing the eight slides to cover the math and special characteristics of ellipses, make pencil drawing of ellipses, introduce the engineering design challenge (the pool table project), review the steps of the engineering design process and clarify the project constraints.
3. Divide the class into engineering teams of three students each.
4. Inform groups of the $10 budget. Tell them that they are free to use any of the instructor-provided materials for their pool table designs—as much as the budget allows.
5. Have students brainstorm and discuss within their groups how they want to build an elliptical pool table, its size, what materials they would use and why they want to use those materials.
6. Students design their own elliptical pool tables. Encourage them to be creative in the design and materials. Remind them of the constraints, including the budget and size limitation.
7. In their groups, students sketch their plans and decide what materials to use.
8. Students begin building to finish up the remainder of the class period.
9. During the second class period, students continue to build their prototype pool tables.

10. Students test and iterate. Provide at least 20 minutes at the end of class for students to test other groups’ tables. Test procedure: Using a cue, hit a ball from one focal point towards the pool table bumper to see if it ends up in the pocket (the second focal point). As time permits, let groups make improvements to their prototype designs.
11. Give each group a few minutes to demonstrate its elliptical pool table to the rest of the class.
12. Conclude with a class discussion to prompt students to reflect on the project. Refer to the suggested question provided in the Assessment section.

Vocabulary/Definitions

constraint: A limitation or restriction. For engineers, design constraints are the requirements and limitations that final design solutions must meet.

ellipse: A geometric figure defined as a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. A circle is a special type of an ellipse in which both focal points are at the same location.

focus: A point used to specify a curve, such as a conic section or other plane curve. For two given points, called the foci, an ellipse is the locus of points such that the sum of the distance to each focus is constant. Plural is foci.

reflexive property: When a ray of light originating from one of the foci reflects off the inner curved surface of an ellipse, it always passes through the other focus. When it meets the point on the ellipse, it reflects off of the tangent to the ellipse and then passes through the other focus.

Assessment

Pre-Activity Assessment

Math Problem: To verify student understanding of the ellipse’s property, have them work in groups to solve the following math problem: Two girls are standing in a whispering gallery shaped like a semi-elliptical arch. The arch height is 30 feet and the width is 100 feet. How far from the center of the room should whispering dishes be placed so that the girls can whisper to each other? (Hint: Whispering dishes are placed at ellipse foci.)

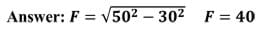
Research: Have students research to find real-life applications that take advantage of or demonstrate the ellipse’s reflection property. Have them take notes so they can report back to the class. Possible examples:

• A machine called lithotripter that is used to crush kidney stones by using shockwaves
• Elliptical reflectors in lamps, such as those used in dentist lamps

Activity Embedded Assessment

Real-Life Applications: Ask students to describe any real-life applications they discovered from their research. Then introduce them to a practical application of an ellipse—an elliptical pool table. Ask them how they might take advantage of the reflective property of an ellipse in order not to miss a shot. Then, ask them to discuss with their team members how they can build an elliptical pool, its size, what materials they would use and why. Have them document the math calculations they use to create their pool tables.

Post-Activity Assessment

Project Reflection: After students test their elliptical pool tables and present them to the class, lead a concluding discussion. Have students consider the following:

• Why did you choose that specific table/ellipse size? (Example answer: With these dimensions, the foci were integers. Answers will vary by group.)
• What effect does the table size have? (Example answer: Larger tables provide many more points on the ellipse curve in which the ball can rebound into the hole. Answer: Expect students to realize that the size and material had no effect.)
• Do any of you have questions to ask other groups about their design decisions and logic?
• What materials did you choose and what effect did they have? What materials worked well? Which did not? What other design decisions were successful or not successful? (Example answers: Our table bumper is too stiff or not stiff enough, causing the ball to rebound inaccurately. Answer: Expect students to realize that the size and material had no effect.)
• How could you apply this in real life, besides a pool table? (Answers: The mathematical and reflexive principles of ellipses can be applied to the creation of whisper chambers and to the explanation of planetary motion. Ask students to use their imaginations and come up with some new ideas, perhaps variations of whispering halls for different purposes or building fun pool table games for kids.)

Activity Scaling

For lower grades, permit students to use more materials, have a larger budget and/or make pool tables larger.

Additional Multimedia Support

As part of the Introduction/Motivation presentation, show students the 1:13-minute online video clip of the whispering gallery in the U.S. Capitol building in Washington DC, at https://www.youtube.com/watch?v=FX6rUU_74kk.

Copyright

Contributors

Supporting Program

Acknowledgements

Created through the University of Houston’s Cullen College of Engineering's NSF Research Experience for Teachers (RET) Program, grant no. EEC 1130006. However, these contents do not necessarily represent the policies of the National Science Foundation and you should not assume endorsement by the federal government.