Hands-on Activity Forces and Graphing

Learning Objectives

After this activity, students should be able to:

• Explain basic concepts about static (not moving) reaction forces.
• Use data analysis tools and explain concepts of plotting engineering data.
• Analyze graphs to determine relationships between variables and rates of change.
• Describe the basic steps in designing an experiment and interpreting results.
• Determine the slope and equation of a line.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• 2-in x 4-in wooden board, 4 feet long
• 2 analog bathroom scales (not digital)
• 2 wooden blocks of the same thickness, each about 6-inches long
• ruler or yardstick
• masking tape
• graph paper
• (optional) Microsoft Excel and computer

Pre-Req Knowledge

Students should know how to:

• Use variables to write a mathematical expression in symbolic form.
• Use equations to represent relationships.
• Analyze patterns and functions by means of words, tables and graphs.

Introduction/Motivation

Some engineers design bridges, skyscrapers and other structures that must support very heavy loads. These loads can be caused by natural phenomena, such as strong winds, the weight of snow or earthquakes. They can also be caused by the use of the structure, such as large trucks that drive across bridges. The loads can also be caused by the weight of the structure itself, such as the weight of the top floor of a building pushing down on the bottom floor. Structural engineers aim to design structures that won't fall down, even when the heaviest loads imaginable are applied. To do this, they make precise predictions and measurements of the loads applied to structures, how forces are distributed inside structures, and how forces are transmitted to the ground. The study of forces on structures that do not move is called statics.

Have you ever seen a weigh station along a highway? Did you ever wonder how they weigh those big 18-wheeler trucks? They don't use a giant scale. Instead, they use several scales and combine the measurements. One-stop axle weighing of a truck uses several scales that work together to determine the axle weight plus the total weight. Each axle (set of wheels) is parked on top of its own scale. The weights recorded by each scale are added together, and the result is the total weight of the truck. You can do the same kind of thing with your car or a table, even if you have only one scale. Put the scale under one wheel/leg, and then record the weight. Then move it to each of the other three wheels/legs, recording the weight applied by each to the ground. When you add up the four weights, you get the total weight of the car/table.

Can you give another example of how math and science relate to engineering? Newton's third law of motion states: "To every action, there is an equal and opposite reaction." The statement means that when one object applies a force on a second object, the second object applies a force on the first of the same size but with opposite direction. Can you relate this law to the work of structural engineers who design bridges? If the bridge is supported by a number of columns, then the bridge applies a downward force to each column. Each column, in response, applies an equal force to the bridge, but in the upward direction. These upward forces are what keep the bridge from falling down. If you add all of the upward forces applied by the columns together, you get a value that is equal to the total weight of the bridge and all the cars and people on it.

Procedure

Before the Activity

• Gather materials
• Practice being able to create charts in Microsfot Excel to represent data.
• Read the article at http://www.Howstuffworks.com to understand a practical application of reaction forces in truck weigh stations.

With the Students

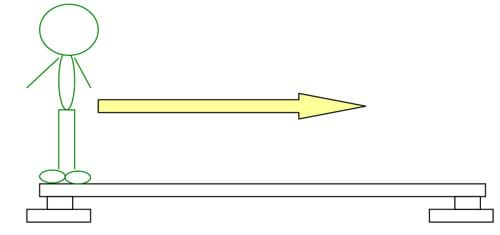
1. Assemble one complete experimental setup with the ends of a 2 x 4 beam resting on two blocks that each rest on a scale, as shown below.

2. Describe the purpose of the experimental set up (for example: "this is the beam") and student expectations. Involve them in a discussion with questions such as:

• Where would I have to stand on this beam if I wanted both scales to read the same value? (Answer: The middle of the beam.) Where would I have to stand if I wanted one scale to read zero? (Answer: Directly over the other scale.) If one scale reads zero, what will the other scale read? (Answer: The person's full weight.)
• We are going to investigate how the forces measured by the scales change when the location of the person on the beam changes. What is the independent variable? (Answer: The position of the person.) What are the dependent variables or what variables respond to changes in the independent variable? (Answer: The forces measured by the scales.)
• An engineer would call the weight of the person the "applied force" or the "load." An engineer would also call the forces measured by the scales the "reaction forces" since they are caused by the load. What shall we call these things?
• Can you predict what will happen to the reaction forces as the load moves from one end of the beam to the other? (Answer: The further the load is located from a scale, the smaller the size of the reaction force measured by that scale.)
• How can a table or graph help us understand the results of our experiments and draw conclusions? (Answer: Tables are used to organize data by categories. Each category may represent an independent or dependent variable. For every value of the independent variable, a corresponding value exists for each of the dependent variables. These are the x and y coordinates, respectively, that can be plotted as a point on the graph. This is how a graph is plotted for each value from the table. Graphs are a useful visual aid in analyzing data since they clearly indicate trends in the data for every dependent variable as well as relationships between these dependent variables.)

3. Tell students that the objective is to "determine how the position of the load affects the reaction forces."
4. Divide the class into groups of 3-5 students each. One student stands on the beam acting as the load, another student helps the "load" person remain steady and balanced on the beam, another student (or two, if available) reads each scale and reports the readings to the data recorder, the fourth member of the team. Each group needs an experimental setup.
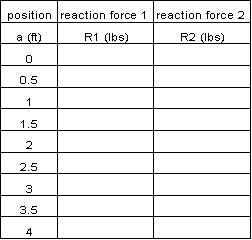
5. Have students create data tables, such as the example in Figure 1.

• Students are not given a worksheet before the experiment is conducted when the purpose is to make them come up with their own table of variables after they have been introduced to the experiment and involved in the preliminary discussions.
• In addition to recording data in tables and drawing graphs, make sure students also understand that they should write down conclusions about the relationship between the variables, trends in the data and predictions about what might happen if the experiment is changed.

6. To conduct the experiment, direct groups to:

• Use a ruler or yardstick to measure the beam and to put a piece of tape on the top of the beam every 6 inches (these marks will be used for measuring load location).
• Place 1 block on the middle of each scale.
• Place the beam onto the blocks.
• Zero the scales. Most analog scales have a wheel to adjust the initial offset of the reading that is due to the weight of the beam. If your scale cannot be zeroed, then record the initial reading and later subtract it from measured values when the load is applied.

7. Ask one person in each group to volunteer to be the load. Have the "load" stand at one end of the beam, and have the rest of the group record the reaction forces. Then, have the load move in 6-inch increments towards the other end of the beam. Record the reaction forces R1, R2, etc., at each location.

8. Create a graph with your data showing load position (a) vs. reaction forces (R1 and R2). What does the graph tell you? Do you notice any patterns in your data? You may have noticed a relationship between R1, R2 and position. How could you show that on the graph? This step can be done by hand using graph paper or on the computer using Mircosoft Excel. It is beneficial for students to approximate a trend line and an equation for each line they graph.

Typical Results

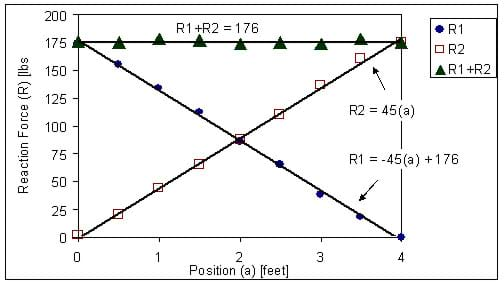
The following results were obtained using a load of 176 lbs. The experimental data obtained is shown in Table 1. In theory, the two reactions add together to give the total weight of the person, regardless of where the person stands. The table shows that some experimental error exists because the total values vary from 175 to 178 lbs. This error may be attributed to problems in reading the scales because it is difficult for the person loading the beam to hold still, and the scales tend to bounce around some. From the data in the table, one can see that as the person moves away from a scale, the value of that reaction force decreases while the other reaction force increases. The same trends are found for different loads.

The data in Table 1 is also shown in the three lines of Graph 1. The first reaction force line starts at a force of 176 lbs. and slopes down toward zero. The second reaction force line starts at zero and increases to 176 lbs. The two lines intersect at around a = 2 ft, which is the midpoint of the beam. This tells us that the reaction forces are equal to each other when the load is placed in the middle of the beam. The third line is the sum of the two reaction forces; it is a horizontal line, indicating that the force of 176 lbs. is approximately constant.

The lines on this graph are trend lines that Microsoft Excel can draw through experimental data. The equations for each line on the graph were obtained from the trend line. For the reaction force R1, the slope of the line is 45 lbs/in and the intercept is 0 lbs. For the reaction force R2, the slope of the line is -45 lbs/in and the intercept is 176 lbs. The slope of reaction force 2 is the negative of the slope of reaction force 1. The lines also have opposite slopes, which tells us that the rate of change is the same for both, but one is increasing and the other is decreasing.

Assessment

Pre-Activity Assessment

Discussion Questions: Solicit, integrate and summarize student responses to the questions in step 2 of the Procedure to assess students' preconceptions. Additional pre-activity assessment questions are:

• What is the difference between weight and mass of an object? (Answer: The force of gravity acting upon an object is sometimes referred to as the weight of an object. The mass of an object refers to the amount of matter that is contained by the object.)
• Newton's third law of motion comes into play when a flying bird strikes an airplane. The bird hits the airplane and the airplane hits the bird. Which of the two forces is greater: the force on the bird or the force on the airplane? (Answer: Each force is the same size/magnitude. The fact that the bird gets injured only means that with its smaller mass, it is less able to endure the greater acceleration forces from the interaction.)

Activity Embedded Assessment

Student Progress: Inspect individual students' tables and charts for completeness.

Post-Activity Assessment

True/False: Ask a true/false question and have students raise their hands if they think the statement is true. Tally the votes and subtract the number from the total number of students to obtain the number who thought the question contains a wrong statement. Write the totals on the board and give the right answer.

• True or False: When a person stood at different positions along the length of the board, the applied force changed. (Answer: False. The applied force is the weight of the person distributed along the beam.)
• True or False: When a person stood at different positions along the length of the board, the reaction forces changed. (Answer: True. The further the load is located from the scale, the smaller the reaction force measured by the scale.)
• True of False: The sum of the two reaction forces is equal to the applied force. (Answer: True. This is a direct application of Newton's third law of motion: "For every action force there is an equal [in size] and opposite [in direction] reaction force." )
• True or False: The trend of the data for the two scale values (reaction forces vs. the position of the load on the beam) from our experiment is linear. (Answer: True. The two reaction forces change proportionately to changes in position.)
• True or False: Weight is a force that is always directed toward the center of the Earth. (Answer: True. Weight is equivalent to the force of gravity, which is directed toward the center of the Earth.)

Open-Ended Questions: Solicit, integrate and summarize student responses to the following open-ended questions:

• Why does a person standing on a beam not fall despite the force of gravity? (Answer: Two forces are acting upon the person. One force, the Earth's gravitational pull, exerts a downward force. The other force, the push of the beam on the person, exerts an upward force. Since these two forces have the same size but opposite direction, they balance each other and the person is at equilibrium.)
• Knowing the difference between mass and weight and that the center of mass of an object is a point at which the mass of the object is concentrated, what is the center of gravity of an object? (Answer: The center of gravity of an object is the place where the weight of an object is concentrated.)

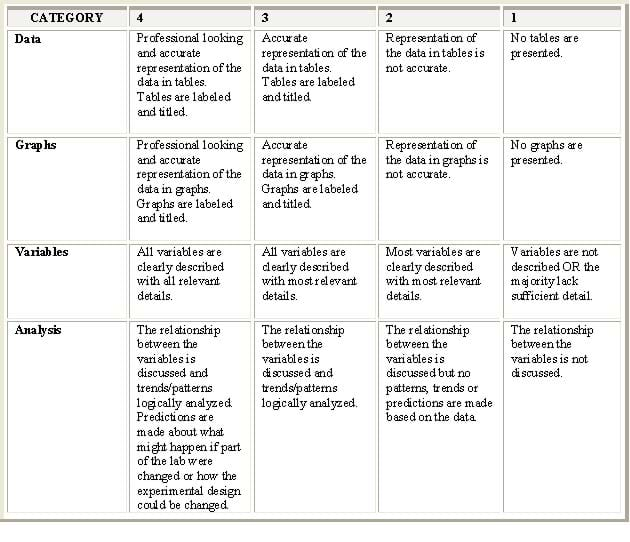
Evaluation Rubric: In addition to the true/false and open-ended questions, use the Table 2 scoring rubric to determine the effectiveness of student work. The rubric is designed to evaluate students' understanding of the purpose of the experiment and the relationship between the variables, organization of data in tables and graphs, and analysis of the results.

Troubleshooting Tips

Not all students may want to be weighed, so ask each group for a volunteer to be the "load" person.

Use analog scales since digital scales automatically switch off after a period of inactivity.

Make sure the person standing on the beam does not lean excessively on a supporting person since this may cause inaccurate measurements by the scales.

If an 8-foot beam is used instead of a 4-foot beam, use more than one block to raise each scale or the beam will bend to the floor under the load.

Activity Extensions

Require students to predict trends in the data before repeating the experiment with beams of different length or thickness. Will the results change if we use an 8-foot instead of a 4-foot beam? After each experiment repetition, compare predictions with actual results.

Additionally, ask students to predict what the graph of the data would be like if the experiment is repeated with a student of a different weight. After each experiment repetition, compare predictions with actual results.

Invite a structural or civil engineer to discuss designing buildings that remain structurally safe and sound during windstorms and tornadoes, or a mechanical engineer to discuss designing automobiles that remain strong and safe during road accidents.

Activity Scaling

• For older or more advanced students, require them to derive the equations for the slope of the lines and their intercept. They could do this in Excel or with graph paper.
• For younger or less advanced students, require them to only graph their results without finding the slope of the lines and their intercept. Then discuss how "steep" the line is and the range of the data, as well as which line is decreasing and which line is increasing.

References

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under National Science Foundation GK-12 grant nos. DGE 0086427 and DGE 0440568. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.