Quick Look
Grade Level: 10 (9-12)
Time Required: 1 hours 45 minutes
(can be split into two 50-minute sessions)
Expendable Cost/Group: US $0.00 This activity requires non-expendable (reusable) coil gun pistols to serve as projectile launchers; see the Materials List for details.
Group Size: 4
Activity Dependency: None
Subject Areas: Physics
NGSS Performance Expectations:

| HS-ETS1-2 |
| HS-PS2-5 |

Summary
Students explore electromagnetism and engineering concepts using optimization techniques to design an efficient magnetic launcher. Groups start by algebraically solving the equations of motion for the velocity at the time when a projectile leaves a launcher. Then they test three different launchers, in which the number of coils used is different, measuring the range and comparing the three designs. Based on these observations, students record similarities and differences and hypothesize on the underling physics. They are introduced to Faraday's law and Lenz's law to explain the physics behind the launcher. Students brainstorm how these principals might be applied to real-world engineering problems.Engineering Connection
This activity introduces students to the idea of goal experimentation. In this case, the goal is to determine the time required to launch a projectile. In the process, students derive equations for analyzing experimental results, test different models for best performance, and then estimate how long it takes to launch the projectile. Then they relate these concepts to real-world engineering challenges.
Learning Objectives
After this activity, students should be able to:
- Find the direction of the magnetic field if the direction of the current is known.
- Determine the direction of an induced current if the direction changing magnetic field is known.
- Determine the time required to launch a projectile.
- Brainstorm real-world engineering applications of these principals.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-2. Design a solution to a complex real-world problem by breaking it down into smaller, more manageable problems that can be solved through engineering. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | Criteria may need to be broken down into simpler ones that can be approached systematically, and decisions about the priority of certain criteria over others (trade-offs) may be needed. Alignment agreement: | |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-5. Plan and conduct an investigation to provide evidence that an electric current can produce a magnetic field and that a changing magnetic field can produce an electric current. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan and conduct an investigation individually and collaboratively to produce data to serve as the basis for evidence, and in the design: decide on types, how much, and accuracy of data needed to produce reliable measurements and consider limitations on the precision of the data (e.g., number of trials, cost, risk, time), and refine the design accordingly. Alignment agreement: | Forces at a distance are explained by fields (gravitational, electric, and magnetic) permeating space that can transfer energy through space. Magnets or electric currents cause magnetic fields; electric charges or changing magnetic fields cause electric fields. Alignment agreement: …and "electrical energy" may mean energy stored in a battery or energy transmitted by electric currents.Alignment agreement: | Empirical evidence is required to differentiate between cause and correlation and make claims about specific causes and effects. Alignment agreement: |
Common Core State Standards - Math
-
Interpret parts of an expression, such as terms, factors, and coefficients.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Factor a quadratic expression to reveal the zeros of the function it defines.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rewrite simple rational expressions in different forms; write a(x /b(x) in the form q(x) + r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division, or, for the more complicated examples, a computer algebra system.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, starting from the assumption that the original equation has a solution. Construct a viable argument to justify a solution method.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve quadratic equations by inspection (e.g., for x² = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a ± bi for real numbers a and b.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve a simple system consisting of a linear equation and a quadratic equation in two variables algebraically and graphically.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use statistics appropriate to the shape of the data distribution to compare center (median, mean) and spread (interquartile range, standard deviation) of two or more different data sets.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy can be grouped into major forms: thermal, radiant, electrical, mechanical, chemical, nuclear, and others.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Analyze how technology transfer occurs when a user applies an existing innovation developed for one function to a different purpose.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- tape measure
- safety glasses, one pair per student
- Magnetic Launcher Worksheet, one per student
To share with the entire class:
- 3 launchers with 30.5 turns
- 3 launchers with 40.5 turns
- 3 launchers with 50.5 turns
- Note: Magnetic launcher (coil gun pistol) kits (and assembly instructions) are available for ~$90 each from Information Unlimited at http://www.amazing1.com/ or http://www.amazing1.com/electric-guns.htm
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/wsu_magnetic_launcher_activity1] to print or download.Introduction/Motivation
(Note to teacher on cultural relevance: Electromagnetism is a staple component of today's society and culture. Magnetic induction is utilized in a variety of technologies and allows magnetic fields to be generated. Solenoids are a technology that runs current through loops of wire to make a strong uniform magnetic field in the middle. One common use of solenoids is in switches; solenoids are used in car starters to temporarily turn on the starter. This project is a hands-on introduction to magnetic fields, spring boarding from a topic everyone is familiar with—projectile motion. Projectile motion occurs whether you kick a ball, throw anything or launch things. This motion is typified by quadratic motion in the y direction while velocity is constant in the x direction.)
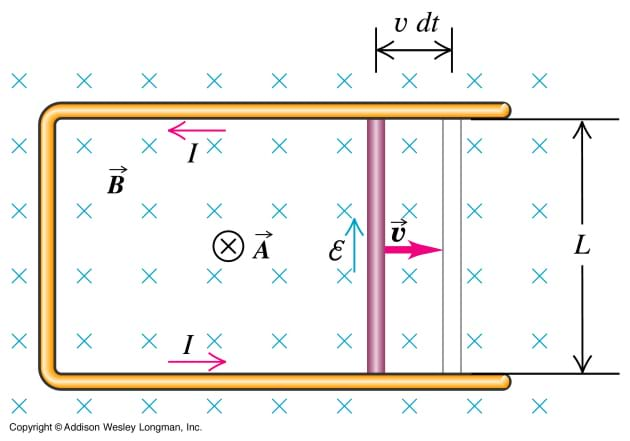
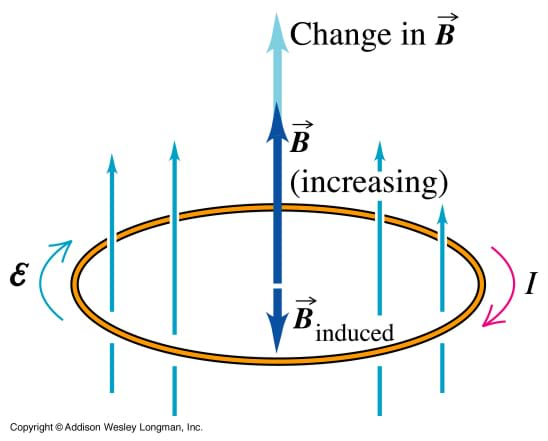
Who can tell me about Michael Faraday and what we call Faraday's law? (Listen to student responses.) Michael Faraday (1791-1867) is a key figure in the study of electricity and an example of one of history's finest experimenters. Faraday's law states that a changing magnetic flux induces a electromotive force and the reverse is true that an electromotive force is proportional to rate of change in the magnetic flux. (For this activity, the focus can be on current and the fact that the current induces a magnetic field and changing magnetic field induces a current.)
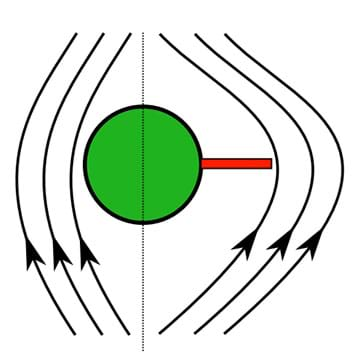
Who can tell me about Heinrich Lenz and what we call Lenz' law? (Listen to student responses.) Russian Heinrich Friedrich Emil Lenz (1804-1865) was a man of many interestes who traveled around the world three times and studied climatic conditions and the physical properties of seawater before focusing on electromagnetism. Lenz's law of electrodynamics states that the direction of the current will be such as to induce a magnetic field in the opposite direction as the magnetic field that induced the current. Lenz's law simply gives direction to the induced current from a changing magnetic field.
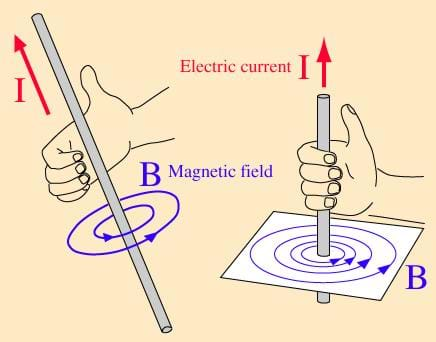
What is the "right-hand rule"? (See if students know.) The right-hand rule is a standard method of relating vectors. We use the right-hand-rule to establish the coordinates in a 3D coordinate system. In other words, it is a quick way to determine the direction of the magnetic field when the current is known (or the opposite). For example, place your fingers in the direction of the x-coordinate with your hand flat, then curl your fingers toward the y-coordinate. The direction of the thumb indicates the positive direction of the z-coordinate.
Procedure
Background
This activity uses electricity, instead of mechanical energy, to launch projectiles. The goal is to have students work with and interact with magnetic. This activity is not meant to be a course in electromagnetism, but rather a way to motivate students to explore what electricity can be used for and get the interested in pursuing a further education in STEM fields. Students are introduced to magnetic induction, induced currents, and some vector basics. They start with the equations of motion to find the initial velocity and then use the launchers and take the experimental data needed to find the initial velocity. Once the initial velocity has been calculated, the initial energy is calculated, and then the acceleration time is calculated.
Moving charges induce a magnetic field. Conversely, changing magnetic fields induce moving charges. This is mathematically explained with Faraday's law, which is described in the Vocabulary section. (One standard form is∇×E ⃗=-(∂B ⃗)/∂t ) Current is a measure of moving charges and has units of coulomb/sec. Lenz's law is used to determine the direction the current is in when induced from a changing magnetic field. These are fundamentally a three-dimensional phenomena, which is why the use of vectors and the right-hand-rule (described above) are needed.
Before the Activity
- Gather materials and make copies of the Magnetic Launcher Worksheet, one per student.
- Assemble the launchers.
With the Students
- Briefly introduce the activity to students, including the goals (see below).
- Hand out the worksheets and let students know that safety glasses are required during experimentation.
- Divide the class into groups of four students each.
- Start by having the students derive an equation for the initial velocity. This is easy once they learn that the initial velocity in the y direction is zero so the velocity in the x direction is equal to the initial velocity.
- Once the equation has been derived, have students start experimentation (see detailed instructions in the next section) and collect data. During the transition from the derivation to the experimentation, ask students what they need in order to calculate the initial velocity. Make sure they understand the connection between the equation they derived and the experiment they are about to perform.
- After students have collected data, have them finish the tables by calculating the initial velocity and then the initial kinetic energy of the projectile. Have students start on the last page of the worksheet.
- Once all students are done with the worksheets, have them talk about Faraday's law and Lenz's law. Ask: Does it make sense? What direction was the current induced in the figures? What was the sequence of events that lead to the launch of the projectile?
- Then, have students talk about the calculated time required for launching the projectile. Ask: What assumptions were made? What things would they change?
- Finally, have students describe how their calculations, experimental data and conclusions can be applied to real-world engineering problems. Provide examples to generate a class discussion.
With the Students -Specific Experimentation Steps
- Start by explaining the two project goals. First, students will learn about projectile motion and the equations that govern projectile motion. Second, they will use magnetic induction to launch projectiles. It is not necessary to talk about how the aluminum rings are launched; this can be done after the experimentation is concluded, or when students start asking how the projectiles are being launched. Prior to going outside and getting data, have students derive an equation for the initial velocity of the projectile given the equations of motion provided below.

There are many ways to solve the equations for the range so that you do not need time. For example, a general solution can be found by solving for time in the stared y equation and then substitute the solution for time into the stared x equation. Then for the case when you fire horizontally, the initial velocity in the y direction is zero and if you start measuring the range from the end of the barrel, x0=0 as well. The final height y=0 and the initial height y0 will be need to be measured while outside. The general range solution is:
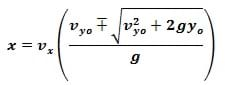
For the case when the projectile is launched horizontally vyo is zero and vx is equal to the initial velocity of the projectile. The range solution reduces to:
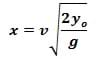
To find the velocity, rearrarnge the equation above for the velocity.
- Go outside and have students measure the range three times for each of the different launchers. Keep in mind that students should fire the launchers horizontally and record the height from the barrel to the ground. Choosing x0 to be zero, measure the range from the end of the barrel to where the projectile first hits the ground.
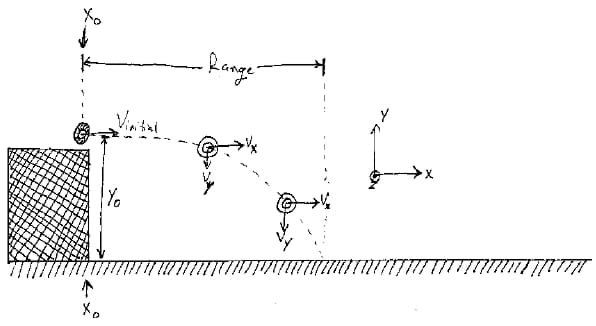
- Go back inside and have students calculate the initial velocity using the equation that they derived earlier. Using the initial velocity, students can calculate the energy deposited into the projectile from the induced current by calculating the initial kinetic energy (K).
![K = 1/2 mv^2 [joules] K = 1/2 mv^2 [joules]](/content/wsu_/activities/wsu_magnetic_launch_activity1/eqn4.jpg)
- Now, talk to the class about how the projectiles were launched. Although the mathematics behind the magnetic induction is somewhat complicated, the idea is not. The launcher stores charge in the two capacitors. When you push the fire button, the charge travels through the coil that is around the barrel. This moving charge, or current, induces a changing magnetic field. Aluminum is a non-magnetic metal, but aluminum is very conductive. The changing magnetic field in the middle of the aluminum ring induces a current. This induced current is such that the magnetic field from this induced current is in the opposite direction as the magnetic field induced from the discharging of the capacitors. Essentially, the aluminum ring is launched by trying to put two magnets together with similar poles.
- The topic of induced currents and magnetic fields can be complicated, but one of the goals is to get students interested in science and engineering. Encourage them to brainstorm examples of how engineers might need to use equations to predict what will happen when launching an object. Have them brainstorm ways engineers might apply what they know about magnetic fields and electric currents. Many online resources provide more about this. The following helpful website has a number of interactive computer simulations that enable students to explore and visualize the phenomena: http://phet.colorado.edu/en/simulations/category/physics/electricity-magnets-and-circuits
Vocabulary/Definitions
electromagnetism: A fundamental force. The study of interactions between electrically charged particles.
Faraday's law: A changing magnetic flux induces a electromotive force and the reverse is true that an electromotive force is proportional to rate of change in the magnetic flux. One standard form is∇×E ⃗=-(∂B ⃗)/∂t, of course for the purpose of this activity, the focus can be on current and the fact that the current induces a magnetic field and changing magnetic field induces a current.
Lenz's law: The direction of the current will be such as to induce a magnetic field in the opposite direction as the magnetic field that induced the current. Lenz's law simply gives direction to the induced current from a changing magnetic field.
right-hand rule: A standard method of relating vectors. Used to determine the direction of the magnetic field when the current is known or the opposite. To determine the direction of the magnetic field, place the right thumb in the direction of the current (I) and the directions the fingers curl indicates the direction of the magnetic field.
Assessment
Worksheet: Have students complete the Magnetic Launcher Worksheet as they work through the calculations, experimentation and analysis. Review their answers to gauge their comprehension of the material.
Investigating Questions
- Why did one launcher work better than the others?
- What engineering design modifications could be made to improve the launch?
- Could more than one coil be used and if so how could that be implemented?
- Is there a better way to calculate the initial velocity?
- Is the projectile accelerated at a constant rate while on the steel rod?
Safety Issues
- All students should wear safety glasses while the magnetic launcher is being used.
- The launchers are electrically safe as long as the black cover is not removed. Do not allow students to remove the magnetic launcher cover.
- When the light becomes illuminated, immediately fire the projectile, otherwise the capacitors continue to charge and this eventually leads to the failure of the magnetic launcher. In addition, this may give inconsistent results when taking measurements of the range.
Troubleshooting Tips
Do not remove the cover while the unit is powered. If the cover needs to be removed for inspection, press the fire button after removing the power and before removing the cover.
Activity Extensions
Once the initial velocity is known, students could change the launch angle from zero and estimate the range and then test.
Activity Scaling
- For lower grades, provide guidance on how to derive some of the equations.
- For upper grades, provide a more through introduction to vectors and a demonstration on how Faraday's law can be expanded and applied to the magnetic launcher.
Additional Multimedia Support
Some very nice interactive simulations are provided at: http://phet.colorado.edu. One in particular looks at Faraday's law and helps students visualize how a magnetic field is being generated: http://phet.colorado.edu/simulations/sims.php?sim=Faradays_Electromagnetic_Lab
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students induce EMF in a coil of wire using magnetic fields. Students review the cross product with respect to magnetic force and introduce magnetic flux, Faraday's law of Induction, Lenz's law, eddy currents, motional EMF and Induced EMF.

Students learn about nondestructive testing, the use of the finite element method (systems of equations) and real-world impacts, and then conduct mini-activities to apply Maxwell’s equations, generate currents, create magnetic fields and solve a system of equations. They see the value of NDE and FEM...
References
Iannini, Bob. Electronic Gadgets for the Evil Genius: 28 Do-It-Yourself Projects. USA: McGraw-Hill, 2004.
Copyright
© 2013 by Regents of the University of Colorado; original © 2009 Board of Regents, Washington State UniversityContributors
Erik WemlingerSupporting Program
CREAM GK-12 Program, Engineering Education Research Center, College of Engineering and Architecture, Washington State UniversityAcknowledgements
This content was developed by the Culturally Relevant Engineering Application in Mathematics (CREAM) Program in the Engineering Education Research Center, College of Engineering and Architecture at Washington State University under National Science Foundation GK-12 grant no. DGE 0538652. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: August 8, 2025





User Comments & Tips