Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Lesson Dependency: None
Subject Areas: Physical Science, Science and Technology
NGSS Performance Expectations:

| MS-PS3-5 |
Summary
Investigating a waterwheel illustrates to students the physical properties of energy. They learn that the concept of work, force acting over a distance, differs from power, which is defined as force acting over a distance over some period of time. Students create a model waterwheel and use it to calculate the amount of power produced and work done.Engineering Connection
While designing elevators, power plants or race cars, mechanical engineers take into consideration the concepts of both work and power. Engineers who design automobile engines consider whether the engine will be used in a high-performance or economical car. A high-performance engine is able to quickly accelerate and has a high power rating; it is also more expensive to manufacture. Thus, an engineer designs an engine for an economical car with a lower power rating to reduce the overall manufacturing cost of the car.
Learning Objectives
After this lesson, students should be able to:
- Make a connection between the concepts of power and work and engineering design.
- Describe how a waterwheel can produce mechanical and electrical power.
- Explain how the concept of the conservation of energy applies to real-world scenarios.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS3-5. Construct, use, and present arguments to support the claim that when the kinetic energy of an object changes, energy is transferred to or from the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Construct, use, and present oral and written arguments supported by empirical evidence and scientific reasoning to support or refute an explanation or a model for a phenomenon. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | When the motion energy of an object changes, there is inevitably some other change in energy at the same time. Alignment agreement: | Energy may take different forms (e.g. energy in fields, thermal energy, energy of motion). Alignment agreement: |
Common Core State Standards - Math
-
Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
(Grade
6)
More Details
Do you agree with this alignment?
-
Evaluate expressions at specific values of their variables. Include expressions that arise from formulas used in real-world problems. Perform arithmetic operations, including those involving whole-number exponents, in the conventional order when there are no parentheses to specify a particular order (Order of Operations).
(Grade
6)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve quadratic equations by inspection (e.g., for x² = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a ± bi for real numbers a and b.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy is the capacity to do work.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Power is the rate at which energy is converted from one form to another or transferred from one place to another, or the rate at which work is done.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Use mathematical expressions to describe the movement of an object
(Grade
8)
More Details
Do you agree with this alignment?
-
Use research-based models to describe energy transfer mechanisms, and predict amounts of energy transferred
(Grade
8)
More Details
Do you agree with this alignment?
Introduction/Motivation
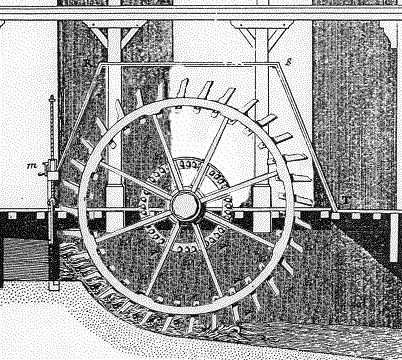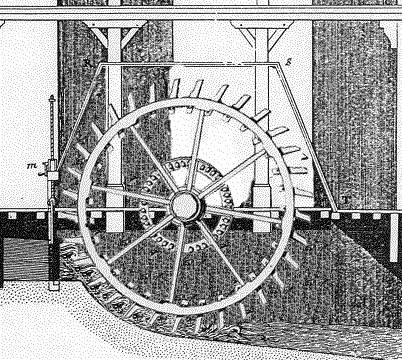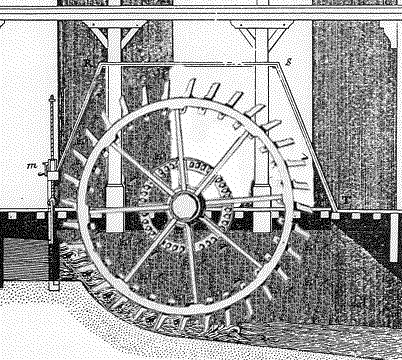
To start this lesson, show the class pictures of waterwheels. Explain that in the past, waterwheels were used to grind grain into flour and saw timber. These processes take advantage of the mechanical energy produced by the spinning axle. Modern hydroelectric power plants use the same waterwheel concept to spin turbines in a dam to produce electricity. Figure 1 shows how flowing water in a dam can spin a rotor.
You can illustrate the concept of using mechanical energy to produce electricity by using a hand generator to power a light bulb. The turbines in a dam provide energy to a generator in the same way and can provide energy for entire cities.
Explain that engineers calculate the power produced by a dam by examining the amount and speed of the flowing water. They can determine how much electricity the turbine can produce and how large an area it can reliably supply with energy. Introduce the associated activity Power, Work and the Waterwheel and explain that the students will do a similar exercise to determine the amount of work a model waterwheel can do and how much power it can generate. Before the activity, present and explain the formulas for work and power that are presented in the Lesson Background section.
Lesson Background and Concepts for Teachers
A brief review of the concepts of potential and kinetic energy (covered in detail in the previous lesson) and work and power, is provided below.
Potential energy is the energy that an object has because of its position. Potential energy can also be thought of as stored energy — energy that an object has, as an inherent characteristic, but is not in use. It is sometimes called gravitational potential energy (PE). It can be expressed mathematically as follows:
PE = mass x g x height
where PE is the potential energy measured in Joules (J) and g is the acceleration due to gravity. At sea level, g = 9.81 meters/sec2. An example of potential energy is a book resting on the edge of a table. If you were to nudge it off the edge of the table, the book would fall to the floor and make a loud noise. This is an expression of kinetic energy. Kinetic energy is the energy an object has because of its motion; any object that is moving has kinetic energy. The falling book in this example is an illustration of kinetic energy. The kinetic energy depends on both mass and velocity and can be expressed mathematically as follows:
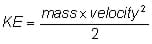
Two new concepts that will be discussed in this lesson are work and power. Work is force acting over a distance and can be expressed as:
Work = force x distance
A Newton (N) is the unit of force in the metric system. To find the weight, or downward force, of an object, simply multiply its mass by gravity. For instance, an object with a mass of 10 kilograms would relate to the following weight:
10 kilograms x 9.81 meters/second2 = 98.1 kilograms*meters/sec2 = 98.1 Newtons.
Now, if a force of 10 Newtons was used to move an object 20 meters, we can determine the work involved. You can visualize this as a person pushing against a big box and sliding it across the floor.
Work = 10 Newtons x 20 meters = 200 Newton*meters = 200 Joules.
A Joule (J) is the unit of work and is the same thing as Newton meter.
Power is work done over a period of time and has units of Watts (W), or Joules/sec. An illustration of power is described in the following example. Two piles of bricks need to be moved across a street. Mary carries two bricks at a time and takes two days to complete the job, while Elizabeth, who is driving a backhoe, does the job in 15 minutes. Mary and Elizabeth both do exactly the same amount of work. However, the amount of power expended is much different. If this job requires 20,000 Joules of work, we can calculate the power of the backhoe. First convert 15 minutes into seconds:
15 min x 60 sec/min = 900 sec.
Then, divide the number of Joules required by the number of seconds:
20,000 Joules ÷ 900 sec = 22.2 Watts.
Elizabeth would then be producing 22.2 Watts of power. On the other hand, Mary would only produce 0.116 Watts of power. Thus, if more power is generated, the quicker the work is performed.
The concepts of work and power are very important to engineers. For example, the power rating of an engine describes how fast a car can accelerate. All cars can go 60 mph, but a sports car such as a Corvette, which has twice the power of most cars, will accelerate to 60 mph very quickly. Engineers need to determine how powerful an engine must be so the car drives well on hills and curves, as well as passes other cars quickly on a freeway. However, powerful engines are costly and if the engine is too expensive, not as many people will buy the car.
Power is also very important in electricity generation. Water will force turbine blades to move and the power of the water will determine the amount of power generated. Engineers can calculate how much power a hydroelectric plant can generate and therefore how large an area or how large a city it can supply with electricity. Power is also important in simpler systems like the operation of building elevators. The amount of power used will determine how quickly an elevator can rise and the maximum weight the elevator can lift.
Associated Activities
- Power, Work and the Waterwheel - Students construct a model waterwheel to generate both power and work.
Lesson Closure

Briefly review the differences between the concepts of power and work. Reiterate that different amounts of power will do the same amount of work over different periods of time (that is, less power takes longer). Show a photograph of a famous dam, like the Hoover Dam, and point out how much potential energy exists at the top of the dam. Talk about the work done by the water on the turbines and the power generated to meet the needs of cities like Phoenix and Las Vegas.
Explain how engineers of all disciplines are needed to work on projects like dams. Civil engineers design and construct the dam, geotechnical engineers monitor the earth that the dam is built upon, environmental engineers monitor the effects of the dam and mitigate the impact of the dam upon the environment, mechanical engineers construct turbines for the wells, and electrical engineers monitor and construct a power grid to provide energy to surrounding cities.
Vocabulary/Definitions
energy: Energy is the capacity to do work (units = Joules).
power: Power is work over a period of time (units = Watts).
work: A force on an object that causes it to move a distance (units = Joules).
Assessment
Pre-Lesson Assessment
Voting: Ask the students to vote on the following questions.
- If a book falls off a table and crashes to the floor, is work done? (Answer: Yes, a force [gravity] acts over a distance [the height of the table].) While just sitting on the table, does a book have potential energy?" (Answer: Yes.) When the book is falling, what kind of energy does it have? (Answer: Kinetic energy.)
- Maria and Jessica are very strong twins. Who does more work: Maria who lifts one block of 100 pounds over a certain distance at a certain speed or Jessica who lifts 10 blocks of 10 pounds over that same distance at the same speed (one at a time)? (Answer: This is a trick question. They both do the same amount of work. The person lifting 10 blocks only uses 1/10th the amount of force to lift the blocks, but travels 10 times as far.)
- Note: For these simplified examples of work, we're not taking into consideration any complicating factors, such as air resistance in moving one's body or when lifting items.
Post-Introduction Assessment
Brainstorming: In small groups, have the students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask the students:
- What might be typical design constraints engineers encounter while trying to decide how powerful they should design a car or elevator system? (Example considerations: How fast does it need to go? What is the heaviest load it will carry? How much will people pay for it? How big can it be? How much fuel or electricity will it use?)
Lesson Summary Assessment
Calculating: Have students practice problems solving for potential energy, kinetic energy, and work:
- If a mass that weighs 8 kg is held at a height of 10 m, what is its potential energy? (Answer: PE = (8 kg)*(9.8 m/s2)*(10 m) = 784 kg*m2/s2 = 784 J)
- Now consider an object with a kinetic energy of 800 J and a mass of 12 kg. What is its velocity? (Answer: v = sqrt(2*KE/m) = sqrt((2 * 800 J)/12 kg) = 11.55 m/s)
- If a force of 20 Newtons is acting over a distance of 6 m, how much work is being done? (Answer: W = 20 N * 6 m = 120 N m)
Question/Answer: Have students answer the following question in a short paragraph in their journals or on a sheet of paper:
- Using the unloading-the-car example in the Pre-Lesson Assessment section, How would you figure out who had more power unloading their grocery bags? (Answer: It depends... whoever finished first had more power.)
Lesson Extension Activities
The following website provides a good description of work and power and also includes interactive exercises: http://www.physicsclassroom.com/Class/energy/U5L1e.html. Have the students read the lessons and work the problems, and check their answers.
Hydroelectric power provides an efficient alternative to traditional electricity sources such as coal and other fossil fuels. Have the students discuss another possible alternative energy source, wind power. Discuss the similarities between wind power and hydroelectric power (i.e., water spins a turbine blade, wind turns a blade on the windmill). Discuss the advantages and disadvantages of these alternative energy sources. Relate that although alternative energy sources are becoming more cost-effective, they are usually more expensive than using fossil fuels. Hydroelectric power, however, is currently cost competitive and cost of wind power is becoming competitive in some regions. An advantage of alternative energy sources is that they are renewable (the sources of fuel do not get used up). Another advantage is that they do not produce pollution like burning fossil fuels do. However, there are some environmental impacts by both wind and water sources. Dams can destroy the ecosystem of a river by changing flows, preventing normal river behavior such as silting and flooding, and preventing fish from getting safely upstream. Wind turbines often spin too fast for birds to see and the birds fly into the turbines and die. Compare the risks of pollution by fossil fuels to the environmental impact of these cleaner fuel sources. The following link provides more detailed information on renewable energy: https://www.nrel.gov/.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

On the topic of energy related to motion, this summary lesson ties together the concepts introduced in the previous four lessons and show how the concepts are interconnected in everyday applications. A hands-on activity demonstrates this idea and reinforces students' math skills in calculating energ...

Students are introduced to both potential energy and kinetic energy as forms of mechanical energy. A hands-on activity demonstrates how potential energy can change into kinetic energy by swinging a pendulum, illustrating the concept of conservation of energy.

Students learn about wind as a source of renewable energy and explore the advantages and disadvantages wind turbines and wind farms. They also learn about the effectiveness of wind turbines in varying weather conditions and how engineers work to create wind power that is cheaper, more reliable and s...

This lesson introduces the concepts of momentum, elastic and inelastic collisions. Many sports and games, such as baseball and ping-pong, illustrate the ideas of momentum and collisions. Students explore these concepts by bouncing assorted balls on different surfaces and calculating the momentum for...
References
Kahan, Peter. Science Explorer: Motion, Forces, and Energy, Upper Saddle River, NJ: Prentice Hall, 2000.
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Bailey Jones; Matt Lundberg; Chris Yakacki; Malinda Schaefer Zarske; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: July 3, 2019









User Comments & Tips