Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| MS-PS3-5 |

Summary
On the topic of energy related to motion, this summary lesson ties together the concepts introduced in the previous four lessons and show how the concepts are interconnected in everyday applications. A hands-on activity demonstrates this idea and reinforces students' math skills in calculating energy, momentum and frictional forces.Engineering Connection
For safety, when designing recreation and transportation vehicles, engineers take into account all of the energy of motion concepts. An engineer designing a scooter cannot focus on one concept, such as momentum, and ignore the effects of friction, mechanical energy or work on the scooter. No one would want to ride a scooter that overcomes friction so well that is does not stop! Consumers benefit from engineers who have a superb understanding of potential energy, kinetic energy, work, power, momentum, collisions, friction and drag.
Learning Objectives
After this lesson, students should be able to:
- Explain the concepts of kinetic and potential energy.
- Explain that energy can change from one form into another.
- Explain the difference between the scientific concepts of power and work.
- Differentiate the different types of friction: static friction, kinetic friction and drag.
- Describe energy, momentum, power and work and friction by equations.
- Calculate the amount of mechanical energy, momentum, power and work and friction in a system.
- Explain why energy of motion concepts are so fundamental to engineering design.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS3-5. Construct, use, and present arguments to support the claim that when the kinetic energy of an object changes, energy is transferred to or from the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Construct, use, and present oral and written arguments supported by empirical evidence and scientific reasoning to support or refute an explanation or a model for a phenomenon. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | When the motion energy of an object changes, there is inevitably some other change in energy at the same time. Alignment agreement: | Energy may take different forms (e.g. energy in fields, thermal energy, energy of motion). Alignment agreement: |
Common Core State Standards - Math
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
(Grade
7)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy is the capacity to do work.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Power is the rate at which energy is converted from one form to another or transferred from one place to another, or the rate at which work is done.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Use mathematical expressions to describe the movement of an object
(Grade
8)
More Details
Do you agree with this alignment?
-
Develop a research-based analysis of different forms of energy and energy transfer
(Grade
8)
More Details
Do you agree with this alignment?
Pre-Req Knowledge
A basic understanding of the concepts of mechanical energy, work and power, momentum, and friction.
Introduction/Motivation
The previous lessons and activities in this unit provided examples that demonstrate the physical science concepts of mechanical energy, work and power, momentum and collisions, and friction and drag, while waterwheels were used as a demonstration of work and power, if you look deeper into a waterwheel system, you will see aspects of mechanical energy, momentum, and friction as well. Water turns the wheel by going from a high potential energy to kinetic energy. Also, if no load existed on the waterwheel and the water supply ran out, the wheel would keep turning, showing signs of momentum. However, friction would eventually bring the wheel to a stop.
In real-world physical systems, these energy of motion concepts are commonly interconnected with each other. Much of our everyday lives and safety depend on engineers designing vehicles and structures with a firm understanding of these concepts and their interaction. Imagine how these concepts interact in the use of skateboards, scooters, roller coasters, trains, cars, planes, trucks, bicycles, elevators, etc. In this lesson, we put all of these concepts together to understand how they work collectively in a hands-on, inclined ramp associated activity Energy in Collisions: Rolling Ramp and Review. (Refer to the associated activity Energy in Collisions: Rolling Ramp and Review (for High School) for more advanced engagement.)
Lesson Background and Concepts for Teachers

PE = mass x g x height and 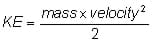
where g is gravity measured as 9.81 meters/sec2 (32.2 feet/sec2) at sea level.
As an object goes from a high to a low position or height, its potential energy is converted into kinetic energy. Naturally, as kinetic energy increases, the objects velocity increases and the object gains momentum. Momentum is defined as:
Momentum = mass x velocity
with units measured in kg-meter/sec. With momentum, two types of collisions exist: elastic collisions, in which momentum is conserved, and inelastic collisions, in which momentum is not conserved. A rubber ball and a ball of silly putty are good examples of objects that experience elastic and inelastic collisions. A rubber ball experiences elastic collisions and the silly putty experiences inelastic collisions.
Imagine you are on a skateboard, coming down a steep hill. You are converting your potential energy into kinetic while gaining momentum. How might you slow down and safely come to a stop without having an inelastic collision with the ground? (Ouch!) Friction and drag could be used to slow you down until you can safely step off of the board. Drag could be maximized by facing your body forward and outstretching your arms (silly looking, but definitely not aerodynamic). If you were a little more daring and needed to stop faster, you could press down on the back of the skateboard so the lip would grind against the ground to take advantage of friction. The force of friction on an object moving on a flat surface is defined as:
FF = μ × W
where FF is the force of friction measured in newtons (N) or pounds (lbs), μ is the coefficient of friction which is unit-less, and W is the weight of the object. μs and μk are used in the cases of static friction and kinetic friction. Work and power were also discussed in previous lessons. Work is defined as force acting over a distance, or:
Work = force × distance
and power is defined as work divided by time, or:
Power = force × distance ÷ time
In the case of the skateboard coming to a stop, friction and drag do the work to bring you to a stop. However, this is a special case because the frictional forces would be acting in a direction opposite to your motion. Normally the force and distance are going in the same direction, which gives a positive value of work. Conversely, the value of work is negative for frictional forces.
Associated Activities
- Energy in Collisions: Rolling Ramp and Review - Students take measurements from a ball and ramp activity that demonstrates the concepts of mechanical energy, work and power, momentum, and friction. They use equations that describe these concepts to calculate unknown variables, and review the relationships between them.
- Energy in Collisions: Rolling Ramp and Review (for High School) - Same experimental activity as the Ramp and Review activity, but with more complexity in the explanations and worksheet problems.
Lesson Closure
Engineers learn these principles of physical science in order to design vehicles for recreation and transportation. From skateboards and scooters to roller coasters and light rail trains, engineers must understand these concepts to design for safety. You would not want a scooter with wheels that do not provide any friction, or climb on a roller coaster that does not have enough momentum to make it back to the start of the ride. On a larger scale, you would not want to be on a train that has too much momentum to stop, or in a car that does not provide an inelastic collision during an accident. You would not want to fly a plane that does not have enough power to take off on the runway, or creates too much drag and runs out of fuel. Much of our everyday lives and safety depends on engineers designing with an understanding of these energy of motion concepts.
Vocabulary/Definitions
coefficient of friction: An experimentally determined value that helps determine the amount of friction experienced between two objects.
conservation of momentum: The amount of momentum in a system remains the same after a collision.
drag: The frictional force that a fluid exerts upon an object traveling though it.
elastic collision: A collision in which all of the momentum is conserved. For example, a ball that bounces back up to its original height.
energy: The capacity to do work. (units = joules)
friction: The force that resists the motion of two objects pressed against each other.
inelastic collision: A collision in which the kinetic energy is not conserved. For example, a ball that only bounces partially to its original height.
kinetic energy: The energy of motion.
kinetic friction: The resistance against an object already moving or sliding.
mechanical energy: Energy composed of both potential energy and kinetic energy.
momentum: Mass in motion. (units = kg-meter/sec)
potential energy: The energy of position, or stored energy.
power: Work over a period of time. (units = watts)
static friction: The resistance against an object to start moving or sliding.
Assessment
Pre-Lesson Assessment
Matching: Create a list of all the equations used in this lesson. Randomly write the left sides of the equations on the left side of the board and the right sides of the equations on the right side of the board. As a class, have the students match the correct sides together. For example,
Momentum mass × g × height
Potential energy force × distance
Vocabulary: Ask students to write down the vocabulary words and definitions on a sheet of paper or in their science journals.
Question/Answer: Have students answer the following questions to gauge their understanding of the lesson concepts.
- What is the relationship between potential and kinetic energy of a falling object? (Answer: The object's potential energy is converted into kinetic as it falls.)
- Does an object's momentum increase while falling? (Answer: Yes)
- What kind of friction does a falling object experience? (Answer: Drag)
Post-Introduction Assessment
Discussion Question: Ask students and discuss as a class how the waterwheel was an example activity that showed a combination of energy, work and power, momentum, and friction. Ask students to suggest another example from the previous energy of motion lessons and activities that also shows a combination of energy, work and power, momentum, and friction. (Example answer: In lesson 4, bobsledders were cited as real-life example of minimizing friction and drag. While going down the track, bobsledders also convert potential energy into kinetic energy. They also gain momentum to carry them through the turns and must have a powerful start when pushing the sled to help decrease their time.)
Lesson Summary Assessment
Pairs Check: Have students work in pairs to answer the following questions.
- If a .2 kg frisbee is 2 meters off the ground and flying at 3 meters/sec, how much total mechanical energy and momentum does it have? (Answer: Mechanical energy = 4.824 Joules. Momentum = .6 kg-m/s. See work, below.) ME = PE + KE = (m × g × h) + (½ × m × V2) ME = (.2 kg × 9.81 m/s2 × 2 m) + (½ × .2 kg × [3 m/s]2) ME = 3.924 J + .9 J ME = 4.824 Joules Momentum = m x V = .2 kg x 3 m/s = .6 kg-m/s
- If it took 66.7 Newtons of force to pick up your cat and place him on a ledge 2 meters high in 3 seconds, how much work did you do? How much power did you have? (Answer: Work = 133.4 Joules. Power = 44.47 Watts. See work, below.) Work = Force × distance = 66.7 N × 2 m = 133.4 Joules Power = Work ÷ time = 133.4 ÷ 3 = 44.47 Watts
- If your cat weighs 66.7 Newtons (or 15 pounds) he has a mass of 6.8 kg. How much potential energy does your cat now have at 2 meters high? (Answer: 133.4 Joules. See work, below.) PE = m × g × h = 6.8 kg × 9.81 m/s2 × 2 m = 133.4 Joules
- Does it make sense that if you exert 133.4 Joules of work to lift your cat 2 meters, that she now has 133.4 Joules of potential energy? (Answer: It should.)
- If you weigh 500 Newtons and are sliding on ice, which has a coefficient of friction of .1 (μ), how much frictional force do your feet feel? (Answer: 50 Newtons. See work, below.) FF = μ × W = .1 × 500 N = 50 Newtons
- Why is work done by friction considered to be negative? (Answer: Work is positive when the force and distance are in the same direction. With friction, the force is always in the opposite direction of motion, hence a negative value of work.)
Lesson Extension Activities
As an open-ended design activity, propose to students that they are engineers hired by an amusement park to design a new roller coaster. Have them sketch their designs and explain how they took mechanical energy, momentum, work and power, and friction into consideration. Remind students that too much or too little of one thing may be disastrous. For example, too much friction, too little momentum or too little potential energy in the beginning cause the ride to stop in the middle of the track. However, too much momentum or kinetic energy might cause the ride to jump off of the track.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

This lesson introduces the concepts of momentum, elastic and inelastic collisions. Many sports and games, such as baseball and ping-pong, illustrate the ideas of momentum and collisions. Students explore these concepts by bouncing assorted balls on different surfaces and calculating the momentum for...

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Students also investigate the psychological phenomenon of momentum; they see how the "big mo" of the bandwagon effect contributes to the development of fads and manias, and how modern technology and mass media accelerate and intensify the effect.
References
Asimov, Isaac. The History of Physics. New York, NY: Walker & Co., 1984.
Jones, Edwin R. and Richard L. Childers. Contemporary College Physics. Reading, MA: Addison-Wesley Publishing Co., 1993.
Kahan, Peter. Science Explorer: Motion, Forces, and Energy. Upper Saddle River, NJ: Prentice Hall, 2000.
Investigation Water Wheel activity. Railroad Commission of Texas. Accessed 2004. http://www.rrc.state.tx.us
The Physics Classroom: Momentum and Its Conservation. Accessed 2004. http://www.physicsclassroom.com/Class/momentum/momtoc.html
Waterwheel Factory. Accessed 2004. http://www.waterwheelfactory.com
Copyright
© 2004 by Regents of the University of ColoradoContributors
Chris Yakacki; Malinda Schaefer Zarske; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under grants from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation (GK-12 grant no. 0338326). However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: June 30, 2019





User Comments & Tips