Quick Look
Grade Level: 10 (9-11)
Time Required: 45 minutes
Expendable Cost/Group: US $5.00
Group Size: 3
Activity Dependency: None
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| HS-PS2-2 |
Summary
In this activity, students examine how different balls react when colliding with different surfaces. Also, they will have plenty of opportunity to learn how to calculate momentum and understand the principle of conservation of momentum.
Engineering Connection
Sports engineering is becoming a popular specialty field of study. While some engineers dedicate their research to understanding collisions between balls and bats, others study the effects of a golf ball colliding with the head of a golf club. And, mechanical engineers consider momentum and collisions when designing vehicles. Learning how the human body and equipment interacts with the ball during impact or how the human body interacts with the inside of a car during a crash, helps engineers design better sports equipment and safer vehicles.
Learning Objectives
After this activity, students should be able to:
- Understand that momentum depends on both mass and velocity.
- Recognize that different surfaces and materials promote different types of collisions.
- Collect data to solve equations.
- Learn that understanding material properties is an important aspect of engineering design
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-2. Use mathematical representations to support the claim that the total momentum of a system of objects is conserved when there is no net force on the system. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use mathematical representations of phenomena to describe explanations. Alignment agreement: | Momentum is defined for a particular frame of reference; it is the mass times the velocity of the object. Alignment agreement: If a system interacts with objects outside itself, the total momentum of the system can change; however, any such change is balanced by changes in the momentum of objects outside the system.Alignment agreement: | When investigating or describing a system, the boundaries and initial conditions of the system need to be defined. Alignment agreement: |
Common Core State Standards - Math
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Reason quantitatively and use units to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve quadratic equations in one variable.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Energy cannot be created nor destroyed; however, it can be converted from one form to another.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Reason quantitatively and use units to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve quadratic equations in one variable.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Gather, analyze and interpret data and create graphs regarding position, velocity and acceleration of moving objects
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Develop, communicate and justify an evidence-based scientific prediction regarding the effects of the action-reaction force pairs on the motion of two interacting objects
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 3 different balls (suggestions: ping-pong ball, tennis ball, racquetball, golf ball, baseball, super ball, clay, billiards ball)
- 3 different bouncing surfaces (suggestions: tile floor, linoleum floor, carpeted floor, wooden block, cinder block)
- kilogram or gram scale
- meter stick
- 3 copies of the Bouncing Balls Worksheet (one per student)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_energy_lesson03_activity3] to print or download.Introduction/Motivation
Momentum can be thought of as mass in motion and is given by the expression:
Momentum = mass x velocity
The amount of momentum an object has depends both on its mass and how fast it is going. For example, a heavier object going the same speed as a lighter object would have greater momentum. Sometimes when moving objects collide into each other, momentum can be transferred from one object to another. There are two types of collisions that relate to momentum: elastic and inelastic.
An elastic collision follows the Law of Conservation of Momentum, which states "the total amount of momentum before a collision is equal to the total amount of momentum after a collision." In addition, the total kinetic energy of the system (all the objects that collide) is conserved during an elastic collision. An elastic collision example might involve a super-bouncy ball; if you were to drop it, it would bounce all the way back up to the original height from which it was dropped. Another elastic collision example may be observed in a game of pool. Watch a moving cue ball hit a resting pool ball. At impact, the cue ball stops, but transfers all of its momentum to the other ball, resulting in the hit ball rolling with the initial speed of the cue ball.
In an inelastic collision, the total momentum of the system is conserved, but the total kinetic energy of the system is not conserved. Instead, the kinetic energy is transferred to another kind of energy such as heat or internal energy. A dropped ball of clay demonstrates an extremely inelastic collision. It does not bounce at all and loses its momentum. Instead, all the energy goes into deforming the ball into a flat blob.
In the real world, there are no purely elastic or inelastic collisions. Rubber balls, pool balls (hitting each other), and ping-pong balls may be assumed extremely elastic, but there is still some bit of inelasticity in their collisions. If there were not, rubber balls would bounce forever. The degree to which something is elastic or inelastic is dependent on the material of the object (see Figure 1).
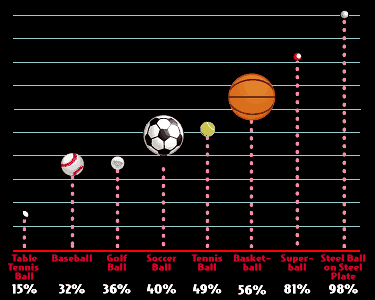
Another way to understand collisions is through Newton's 3rd Law, which tells us that "for every action, there is an equal and opposite reaction". When a cue ball collides with another pool ball, the cue ball exerts a force on the stationary pool ball in the direction that the cue ball is traveling, while the stationary pool ball exerts an equal and opposite force on the cue ball. This is the reason that after the cue ball collides with a stationary pool ball, it sometimes moves in a new direction, sometimes leading to a "scratch". Understanding Newton's 3rd Law, momentum and elastic and inelastic collisions provides a new understanding of our physical world that is full of motion and collisions.
In order to complete this activity, you will also need to have an understanding of the motion of an object. Following are the Kinematics equations:
d = (Vf + Vi) * t
Vf = Vi + at
d = Vi * t + ½ * a * t2
Vf2 = Vi2 + 2 * a * d
Where d is the displacement of an object, Vi is the initial velocity of the object, Vf is the final velocity, a is the acceleration of the object, and t is the interval of time the object traveled. For example, if a ball is rolled off of a table 1 meter above the ground, we can find the velocity with which it hits the floor and the time it takes to do so:
d = 1 m Vi = 0 m/s a = 9.81 m/s2 Vf = ? t = ?
d = Vi * t + ½ * a * t2
¬1 m = 0 m/s * t + ½ * 9.81 m/s2 * t2
t = 0.45 s
Vf2 = Vi2 + 2 * a * d
Vf2 = 0 m/s + 2 * 9.81 m/s2 * 1 m
Vf = 4.43 m/s
If we have three known values, then we must choose equations that use the three values that actually we do have to find the ones that we do not. You also have to read between the lines sometimes to get three known values. For example, in the problem stated previously, the value of acceleration is not given but the object is in free fall, meaning its acceleration is that of gravity.
Procedure
Before the Activity
- Gather materials.
- Make enough copies of the Bouncing Balls Worksheet so that each student has one.
With the Students
- Determine the mass in kilograms of each ball and record it on the data sheet.
- Drop each ball from a distance of 1 meter onto the surface and record how high it bounces in meters (example: 0.46 meters).
- Note whether the ball and surface showed more of an elastic or inelastic collision.
- If the ball bounces up more than .5 meters, then it is more elastic.
- If it bounces up less than .5 meters, then it is more inelastic.
- Repeat steps 1, 2 and 3 for the two other surfaces.
- Calculate the velocity for each ball right before it bounces (question 2) and right after it bounces (question 3).
- Calculate the momentum for each ball right before it bounces (question 4) and right after (question 5).
- Calculate the percentage of momentum lost for each case (question 6).
- Answer the Further Learning questions on the worksheet based on your answers. (Note: Have students complete question 11 as a group.)
- Once the class is finished with the Bouncing Balls Worksheet, discuss which balls had the best elastic collisions on each surface. Also, if time permits go over some of the Further Learning questions as a class.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have the students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask the students:
- What are sports examples of transfer and conservation of momentum? (Possible answers: Hitting a baseball with a bat, hitting the cue ball with a pool stick, the cue ball bouncing off another ball, striking a golf ball with a club or driver, or hitting a tennis ball with a racquet.)
Activity Embedded Assessment
Voting: Ask the students to vote to rank the sports (named above) from those having the greatest momentum to those having the least momentum. While the students will have to use their own judgment, remind them that momentum depends equally on mass and velocity.
Post-Activity Assessment
Problem Solving: Present the class with the following cases:
- Case 1: A big-time slugger hits a baseball 60 meters/sec (134 mph).
- Case 2: Johnny knocks down four pins at the Bowl-a-Rena by rolling a 15-pound bowling ball 1.34 meters/sec (3 mph).
Ask students which ball would bounce higher if each were thrown onto a trampoline with the given velocities. What about on concrete? (Answer: The bowling ball would bounce higher on the trampoline, while the baseball would bounce higher off of concrete.)
Discuss as a class why this is the case. Notice that the trampoline responds with a higher bounce to objects of greater mass, while the concrete causes objects with greater elasticity to bounce higher.
Safety Issues
Be sure the students do not use the balls as projectiles.
Troubleshooting Tips
This activity is best done in groups, because while one person drops the ball, another person must watch the ball and meter stick to note how high the ball bounces. Additional team members could hold the meter stick steady and/or record the data. It is difficult to get an accurate measurement for how high the ball bounces since it is in constant motion. Therefore, have students drop each ball on each surface several times, or until they have a consistent measurement.
Some balls are greatly affected by wind resistance, such as wiffle balls. Therefore, try to pick balls that will not have much influence from wind resistance since this experiment is done under the assumption there exists no wind resistance.
If students have never seen the kinematics equations, this can be a good introduction. Help the students figure out the exact equations they will need to use and walk them through the parts of the worksheets that involve the kinematics equations.
Activity Extensions
Students could investigate the materials used to make balls as a way to better understand why they bounce the way they do. For example, if you cut open a golf ball, you will find a mass of rubber bands wound around a core that is also usually rubber. All that rubber (and the hard plastic cover) explains its bounciness. A baseball has a similar construction, but with very different materials. A baseball's inside is a mass of yarn wound around a cork core, and its cover material is leather. These materials make for a less bouncy ball. (Note: safety precautions should be taken when opening these balls and should be done under adult supervision.)
Activity Scaling
- If there is not enough time to complete the worksheet, have students finish it for homework.
- If students are new to the material and still unfamiliar with the equations they need for this activity, provide them the necessary equations.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students also investigate the psychological phenomenon of momentum; they see how the "big mo" of the bandwagon effect contributes to the development of fads and manias, and how modern technology and mass media accelerate and intensify the effect.

This lesson introduces the concepts of momentum, elastic and inelastic collisions. Many sports and games, such as baseball and ping-pong, illustrate the ideas of momentum and collisions. Students explore these concepts by bouncing assorted balls on different surfaces and calculating the momentum for...

Students examine how different balls react when colliding with different surfaces, giving plenty of opportunity for them to see the difference between elastic and inelastic collisions, learn how to calculate momentum, and understand the principle of conservation of momentum.

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...
References
The Physics Classroom and Mathsoft Engineering & Education, Inc., 2004, accessed May 30, 2007. http://www.physicsclassroom.com/Class/momentum/momtoc.html
Momentum and energy loss of balls colliding against different surfaces, accessed May 30, 2007. http://www.iit.edu/~smile/ph8709.html
The Exploratorium, Science of Baseball, accessed May 30, 2007. http://www.exploratorium.edu/baseball/index.html
The Exploratorium, Science of Baseball, accessed May 30, 2007. http://www.exploratorium.edu/baseball/howfar7.html
The Exploratorium, Science of Baseball, accessed May 30, 2007. http://www.exploratorium.edu/baseball/howfar5.html
Other Related Information
Browse the NGSS Engineering-aligned Physics Curriculum hub for additional Physics and Physical Science curriculum featuring Engineering.
Copyright
© 2007 by Regents of the University of Colorado.Contributors
Bailey Jones; Matt Lundberg; Chris Yakacki; Malinda Schaefer Zarske; Denise Carlson; Ben Sprague; Janet YowellSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: January 14, 2021









User Comments & Tips