Quick Look
Grade Level: 8 (6-8)
Time Required: 45 minutes
Expendable Cost/Group: US $5.00
Group Size: 3
Activity Dependency: None
Subject Areas: Physical Science, Physics
Summary
Students examine how different balls react when colliding with different surfaces, giving plenty of opportunity for them to see the difference between elastic and inelastic collisions, learn how to calculate momentum, and understand the principle of conservation of momentum.
Engineering Connection
Sports engineering is becoming a popular specialty field of study. Some engineers dedicate their research to understanding collisions between balls and bats; others study the effects of a golf ball colliding with the head of a golf club. Mechanical engineers consider momentum and collisions when designing vehicles. Learning how the human body and equipment interacts with the ball during impact or how the human body interacts with the inside of a car during a crash, helps engineers design better sports equipment and safer vehicles.
Learning Objectives
After this activity, students should be able to:
- Understand that momentum depends on both mass and velocity.
- Recognize that difference surfaces and materials promote different types of collisions.
- Collect data to solve equations.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
For any pair of interacting objects, the force exerted by the first object on the second object is equal in strength to the force that the second object exerts on the first, but in the opposite direction (Newton's third law).
(Grades 6 - 8)
More Details
Do you agree with this alignment?
-
Models can be used to represent systems and their interactions—such as inputs, processes and outputs—and energy and matter flows within systems.
(Grades 6 - 8)
More Details
Do you agree with this alignment?
-
The motion of an object is determined by the sum of the forces acting on it; if the total force on the object is not zero, its motion will change. The greater the mass of the object, the greater the force needed to achieve the same change in motion. For any given object, a larger force causes a larger change in motion.
(Grades 6 - 8)
More Details
Do you agree with this alignment?
Common Core State Standards - Math
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Display numerical data in plots on a number line, including dot plots, histograms, and box plots.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations in one variable.
(Grade
8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Fluently add, subtract, multiply, and divide multidigit decimals using standard algorithms for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Display numerical data in plots on a number line, including dot plots, histograms, and box plots.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations in one variable.
(Grade
8)
More Details
Do you agree with this alignment?
Colorado - Science
-
Predict and evaluate the movement of an object by examining the forces applied to it
(Grade
8)
More Details
Do you agree with this alignment?
-
Use mathematical expressions to describe the movement of an object
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 3 different balls (Suggestions: ping-pong ball, tennis ball, racquetball, golf ball, baseball, super ball, clay, billiards ball)
- 3 different bouncing surfaces (Suggestions: tile floor, linoleum floor, carpeted floor, wooden block, cinder block)
- kilogram or gram scale
- meter stick
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_energy_lesson03_activity1] to print or download.Introduction/Motivation
Momentum can be thought of as 'mass in motion' and is given by the expression:
Momentum = mass x velocity
The amount of momentum an object has depends both on its mass and how fast it is going. For example, a heavier object going the same speed as a lighter object would have greater momentum. Sometimes when moving objects collide into each other, momentum can be transferred from one object to another. There are two types of collisions that relate to momentum: elastic and inelastic.
An elastic collision follows the Law of Conservation of Momentum, which states "the total amount of momentum before a collision is equal to the total amount of momentum after a collision." In addition, the total kinetic energy of the system (all the objects that collide) is conserved during an elastic collision. An elastic collision example might involve a super-bouncy ball; if you were to drop it, it would bounce all the way back up to the original height from which it was dropped. Another elastic collision example may be observed in a game of pool. Watch a moving cue ball hit a resting pool ball. At impact, the cue ball stops, but transfers all of its momentum to the other ball, resulting in the hit ball rolling with the initial speed of the cue ball.
In an inelastic collision, the total momentum of the system is conserved, but the total kinetic energy of the system is not conserved. Instead, the kinetic energy is transferred to another kind of energy such as heat or internal energy. A dropped ball of clay demonstrates an extremely inelastic collision. It does not bounce at all and loses its kinetic energy. Instead, all the energy goes into deforming the ball into a flat blob.
In the real world, there are no purely elastic or inelastic collisions. Rubber balls, pool balls (hitting each other), and ping-pong balls may be assumed extremely elastic, but there is still some bit of inelasticity in their collisions. If there were not, rubber balls would bounce forever. The degree to which something is elastic or inelastic is dependent on the material of the object.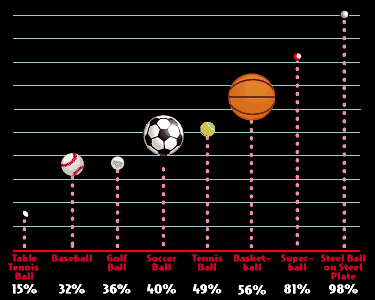
Many sports incorporate collisions and momentum as part of game play. Can you think of some? Certain sports rely primarily on elastic collisions that conserve momentum, such as pool or billiards, while others use inelastic collisions to make the game more challenging. What would happen if a baseball and a bat had an elastic collision like a golf ball and club? (Answer: There would be a lot more home runs during a game!) Another way to understand collisions is through Newton's 3rd Law, which tells us that "for every action, there is an equal and opposite reaction". When a cue ball collides with another pool ball, the cue ball exerts a force on the stationary pool ball in the direction that the cue ball is traveling, while the stationary pool ball exerts an equal and opposite force on the cue ball. This is the reason that after the cue ball collides with a stationary pool ball, it sometimes moves in a new direction, sometimes leading to a "scratch". Understanding Newton's 3rd Law, momentum and elastic and inelastic collisions provides a new understanding of our physical world that is full of motion and collisions.
Procedure
Before the Activity
- Gather materials.
- Print enough for one Bouncing Balls Worksheet per group.
With the Students
- Determine the mass in kilograms of each ball and record it on the data sheet.
- Drop each ball from a distance of 1 meter onto the surface and record how high it bounces in meters (Example: .46 meters).
- Note whether the ball and surface showed more of an elastic or inelastic collision.
- If the ball bounces up more than .5 meter then, it is more elastic.
- If it bounces up less than .5 meter, then it is more inelastic.
- Repeat steps 1, 2 and 3 for the two other surfaces.
- Calculate the momentum for each ball at the point that it bounces, and record on the worksheet. Do one example calculation as a class.
- Note: The momentum calculation is independent of the bouncing surface, so it only needs to be calculated once for each ball.
- Equation: Momentum = mass x velocity
Use the mass determined in step 1. In this example, use .05 kilograms for the mass. Next, determine the velocity of the object when it hits the ground. Velocity of a falling object can be described as:
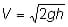
where g is gravity (9.81 m/s2) and h is height (1 m).
Momentum = .05 kilograms x 4.43 meters/second = .222 kg•m/s.
Note: All the balls will have the same velocity because any object dropped from the same height will fall at the same constant rate due to gravity. So, for this activity, the velocity is: 4.43 m/s.
- Once the class is finished with the worksheets, discuss which balls had the best elastic collisions on each surface. Finally, ask the students if they think elastic collisions are more determined by the surface or the momentum.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have the students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask the students:
- What are sports examples of transfer (and conservation) of momentum. (Possible answers: Hitting a baseball with a bat, hitting the cue ball with a pool stick, the cue ball bouncing off another ball, striking a golf ball with a club or driver, or hitting a tennis ball with a racquet.)
Activity Embedded Assessment
Voting: Ask the students to vote to rank the sports (named above) from those having the greatest momentum to those having the least momentum. While the students will have to use their own judgment, remind them that momentum depends equally on mass and velocity.
Post-Activity Assessment
Graphing: As a class make two separate bar graphs—one for momentum and one for velocity. Put the surface type on the x-axis, and the velocity and momentum on the y-axis (for each respective graph). Then make three different colored plots on each graph representing the different ball types. Use these graphs to visually represent which balls had the most elastic collisions and on which surface they occurred.
Problem Solving: Present the class with the following problems and ask the students to calculate which case has the greater momentum.
- Case 1: A big-time slugger hits a 0.14 kilogram (5 ounce) baseball 45 meters/sec (100 mph). (Answer: Momentum = mass x velocity = .14 kg x 45 m/s = 6.3 kg•m/s.)
- Case 2: Uncle Cracker knocks down four pins at the Bowl-a-Rena by rolling a 7.3 kilogram (16 pound) ball 4.5 meters/sec (10 mph). (Answer: Momentum = mass x velocity = 7.3 kg x 4.5 m/s = 32.9 kg•m/s.)
- Solution: Uncle Cracker gave the bowling ball much more momentum.
Safety Issues
Be sure the students do not use the balls as projectiles.
Troubleshooting Tips
This activity is best done in groups, because while one person drops the ball, another person must watch the ball and meter stick to note how high the ball bounces. Additional team members could hold the meter stick steady and/or record the data.
For the momentum calculation, note that all the balls will have the same velocity because any object dropped from the same height will fall at the same constant rate due to gravity.
Activity Extensions
Students could investigate the materials used to make balls as a way to better understand why they bounce the way they do. For example, if you cut open a golf ball, you will find a mass of rubber bands wound around a core that is also usually rubber. All that rubber (and the hard plastic cover) explains its bounciness. A baseball has a similar construction, but with very different materials. A baseball's inside is a mass of yarn wound around a cork core, and its cover material is leather. These materials make for a less bouncy ball. (Note: safety precautions should be taken when opening these balls and should be done under adult supervision.)
Activity Scaling
- For lower grades, leave out the part where the students calculate momentum in the activity and focus more on elastic and inelastic collisions. Students should still understand the concept of momentum without actually calculating it. As a class, work the simpler examples in the Assessment section on the board, or have the students complete them individually or with a calculator.
- For upper grades, calculate the momentum in the activity as an individual exercise. Have the students write out their steps when solving the mathematical equations. Assign the students to work the problems in the Assessment section individually.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

This lesson introduces the concepts of momentum, elastic and inelastic collisions. Many sports and games, such as baseball and ping-pong, illustrate the ideas of momentum and collisions. Students explore these concepts by bouncing assorted balls on different surfaces and calculating the momentum for...

In this activity, students examine how different balls react when colliding with different surfaces. They learn how to calculate momentum and understand the principle of conservation of momentum.

Students also investigate the psychological phenomenon of momentum; they see how the "big mo" of the bandwagon effect contributes to the development of fads and manias, and how modern technology and mass media accelerate and intensify the effect.

On the topic of energy related to motion, this summary lesson ties together the concepts introduced in the previous four lessons and show how the concepts are interconnected in everyday applications. A hands-on activity demonstrates this idea and reinforces students' math skills in calculating energ...
References
Momentum:http://www.physicsclassroom.com/Class/momentum/momtoc.html
Momentum and energy loss of balls colliding against different surfaces: http://www.iit.edu/~smile/ph8709.html
Science of Baseball, The Exploratorium: http://www.exploratorium.edu/baseball/index.html
Science of Baseball, The Exploratorium: http://www.exploratorium.edu/baseball/howfar7.html
Science of Baseball, The Exploratorium: http://www.exploratorium.edu/baseball/howfar5.html
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Bailey Jones; Matt Lundberg; Chris Yakacki; Malinda Schaefer Zarske; Denise CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: August 28, 2023






User Comments & Tips