Quick Look
Grade Level: 7 (6-8)
Time Required: 1 hour
Expendable Cost/Group: US $7.00
Group Size: 3
Activity Dependency: None
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| MS-PS3-5 |

Summary
In this hands-on activity—rolling a ball down an incline and having it collide into a cup—the concepts of mechanical energy, work and power, momentum, and friction are all demonstrated. During the activity, students take measurements and use equations that describe these energy of motion concepts to calculate unknown variables, and review the relationships between these concepts.Engineering Connection
Light rail trains are a modern form of public transportation powered by overhead electrical lines that travel along dedicated pathway of steel rails. To design these trains to be quiet, efficient and safe, engineers consider all of the energy of motion concepts: the work required to convert the mechanical energy when the train goes from a stopped position to forward/backward motion, how much momentum the train acquires between stations, and the power required to overcome the friction between the train's wheels and the effects of drag.
Learning Objectives
After this activity, students should be able to:
- Identify components of mechanical energy, work and power, momentum, and friction and how they interrelate.
- Construct a model to demonstrate potential and kinetic energy, work, power, momentum and friction.
- Use multiple equations to solve for unknown variables.
- Explain how the concepts of mechanical energy, work, power, momentum, and friction play an important role in everyday life
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS3-5. Construct, use, and present arguments to support the claim that when the kinetic energy of an object changes, energy is transferred to or from the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Construct, use, and present oral and written arguments supported by empirical evidence and scientific reasoning to support or refute an explanation or a model for a phenomenon. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | When the motion energy of an object changes, there is inevitably some other change in energy at the same time. Alignment agreement: | Energy may take different forms (e.g. energy in fields, thermal energy, energy of motion). Alignment agreement: |
Common Core State Standards - Math
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-life and mathematical problems using numerical and algebraic expressions and equations.
(Grade
7)
More Details
Do you agree with this alignment?
-
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations in one variable.
(Grade
8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy is the capacity to do work.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Fluently add, subtract, multiply, and divide multidigit decimals using standard algorithms for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Variables are used to represent unknown quantities within equations and inequalities.
(Grade
6)
More Details
Do you agree with this alignment?
-
Equations and expressions model quantitative relationships and phenomena.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations in one variable.
(Grade
8)
More Details
Do you agree with this alignment?
Colorado - Science
-
Predict and evaluate the movement of an object by examining the forces applied to it
(Grade
8)
More Details
Do you agree with this alignment?
-
Gather, analyze, and interpret data to describe the different forms of energy and energy transfer
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- yardstick (for the activity setup)
- metric ruler (for measuring distance)
- 4 dowel rods, 3 ft long, ¼-inch thick
- golf ball (or similar sized ball)
- plastic or Styrofoam cup (must be lightweight, not heavy)
- scale (to weigh the golf ball)
- tape
- paper towels or tissues
- Ramp and Review Worksheet
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_energy_lesson05_activity1] to print or download.Introduction/Motivation
Picture yourself atop a big hill with a scooter. Do you know how much potential energy you have? How fast will you be going when you reach the bottom? How much momentum will you have at the bottom? If you press hard on your brakes and slide to a stop, how much work will friction have done? Today's activity models this scenario and helps you answer these questions.
Procedure
Before the Activity
- Gather materials and make copies of the Ramp and Review Worksheet, one per group.
- (optional) Set up a demo test station to help students visualize how the pieces go together.
With the Students

- Divide the class into teams of two to four students each. Hand out the materials.
- Tape a dowel rod to each side of a yardstick, approximately 1-inch apart from each other. This serves as a track for the golf ball to roll down.
- Prop the yardstick against a wall or desk to create a slope for the ball to roll down.
- Place a small amount of crushed paper towels or tissues inside the cup to absorb the impact of the ball and keep the ball in the cup.
- Place the cup at the end of the yardstick ramp to catch the ball at the end of the incline.
- Tape the other two dowel rods a few inches apart to create a track for the cup to slide along.
- On the worksheet, complete questions 1 and 2 (measure the height of yardstick and weight of golf ball).
- Place the ball at the top of the ramp and let it go.
- Measure the distance the cup travels at the end of the ramp and record that for question 3 on the worksheet.
- Complete the calculations on the worksheet.
- Conclude with a class discussion. See the Assessment section for details.
Assessment
Pre-Activity Assessment
Brainstorming: Have students engage in open discussion. Remind them that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask students to think of situations that involve a combination of mechanical energy, momentum and collisions, work and power, and friction. (Example answer: Going down a slide. Potential energy turns into kinetic energy. Friction from sliding. As you gain velocity, you gain momentum.)
Activity Embedded Assessment
Worksheet: Have students use the Ramp and Review Worksheet to record measurements and follow along with the activity. After teams have finished their worksheets, have them compare answers with their peers.
Hypothesize: Ask each group what would happen if a heavier glass cup was used instead of a lightweight cup. (Answer: The heavier cup would slow the overall speed of the ball and cup to conserve momentum. Since the lightweight cup is used, the ball and cup will barely slow down to conserve momentum.)
Post-Activity Assessment
Worksheet Discussion: As a class, review and discuss the worksheet answers. Student answers reveal their level of mastery of the concepts.
Discussion Questions: As a class, solicit, integrate and summarize student responses to the following wrap-up questions, which refer to question 8 on the worksheet:
- Why is work expressed as a negative value? (Answer: Work is defined as "force acting over a distance." When the force and distance traveled are in the same direction, the value of work is positive. However, in this case of friction, the force is acting in the opposite direction of the sliding cup, hence a negative value of work.)
- How did the friction, momentum, kinetic and potential energy, and work and power all come together to make the cup move? How does this relate to activities you do every day? (Answer: To make the cup move, first we built up momentum by giving the ball potential energy and converting it into kinetic energy. When the ball reached the bottom of the track, it collided with the cup and conserved momentum. Once the cup started sliding, friction came into play to bring the cup to a stop. The power of friction was related to how fast the cup stopped. This is very similar to riding down a hill with a bicycle, skateboard or scooter and braking to come to a stop.)
Troubleshooting Tips
If the ball falls out of the cup,
- A small amount of wadded tissues or paper towels in the bottom of the cup helps to catch the ball and keep it in the cup
- Adjust the slide rails so that the cup does not turn around while sliding.
- Make sure the cup is placed on a smooth surface and not on carpet.
- If the yardstick is angled too high or too low, the cup will not slide as well as it could. Adjust the yardstick to approximately a 30˚ – 40˚ angle.
Activity Extensions
Another form of mechanical energy is rotational energy, which has not been discussed in this unit. In actuality, as the ball rolls down the incline, some of the potential energy is turned into rotational energy, while the rest is turned into kinetic energy. This decreases the ball's velocity as it rolls down the incline and makes our calculated value of velocity slightly higher than it really is. Have students search the Internet to find out more about rotational energy and why it causes certain objects to roll slower down inclines. Start with the rotational energy article at Wikipedia: https://en.wikipedia.org/wiki/Rotational_energy.
Activity Scaling
- For lower grades, have students complete at least one trial of how far the cup slides and record that on the worksheet as their distance (question 3). Also, you may want to run through the equations (on the bottom of the worksheet) as a class. Worksheet question 6 may be difficult, so solve it together.
- For upper grades, have students solve for velocity using the kinetic energy equation on their own. (Conduct the high school version of this activity.) For example,
K.E. = ½ ∙ m ∙ V2 → 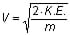
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

In this hands-on activity—rolling a ball down an incline and having it collide into a cup—the concepts of mechanical energy, work and power, momentum, and friction are all demonstrated. During the activity, students take measurements and use equations that describe these energy of motion concepts to...

On the topic of energy related to motion, this summary lesson ties together the concepts introduced in the previous four lessons and show how the concepts are interconnected in everyday applications. A hands-on activity demonstrates this idea and reinforces students' math skills in calculating energ...

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...
Copyright
© 2004 by Regents of the University of ColoradoContributors
Chris Yakacki; Malinda Schaefer Zarske; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under grants from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation (GK-12 grant no. 0338326). However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: January 23, 2020









User Comments & Tips