Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Lesson Dependency: None
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| HS-PS2-2 |

Summary
As a continuation of the theme of potential and kinetic energy, this lesson introduces the concepts of momentum, elastic and inelastic collisions. Many sports and games, such as baseball and ping-pong, illustrate the ideas of momentum and collisions. Students can use the associated activities to explore these concepts by bouncing assorted balls on different surfaces and calculating the momentum for each ball.Engineering Connection
Crunch! That is the sound that you hear when two cars crash into each other. This unnerving sound can be a good thing if it is the sound of a wonderful safety innovation developed by engineers, called the crumple zone. Mechanical engineers consider momentum and collisions when designing vehicles. A crumple zone is designed into motor vehicles to absorb the main impact of the energy being transferred during a crash, so the people inside don't get hurt. Airbags are another engineering safety improvement to protect passengers from the impact of collisions.
Learning Objectives
After this lesson, students should be able to:
- Calculate the momentum of a moving object.
- Recognize that momentum is proportional to mass and velocity.
- Explain that in a closed system, momentum is conserved in both elastic and inelastic collisions.
- Describe how collisions and momentum play an important role in the design of safe automobiles.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-2. Use mathematical representations to support the claim that the total momentum of a system of objects is conserved when there is no net force on the system. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use mathematical representations of phenomena to describe explanations. Alignment agreement: | Momentum is defined for a particular frame of reference; it is the mass times the velocity of the object. Alignment agreement: If a system interacts with objects outside itself, the total momentum of the system can change; however, any such change is balanced by changes in the momentum of objects outside the system.Alignment agreement: | When investigating or describing a system, the boundaries and initial conditions of the system need to be defined. Alignment agreement: |
Common Core State Standards - Math
-
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations in one variable.
(Grade
8)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Use mathematical expressions to describe the movement of an object
(Grade
8)
More Details
Do you agree with this alignment?
-
Gather, analyze, and interpret data to describe the different forms of energy and energy transfer
(Grade
8)
More Details
Do you agree with this alignment?
Introduction/Motivation
The concept of momentum is often used in sports. An announcer might say, "The Denver Nuggets really have some momentum going into the fourth quarter!" or a newspaper headline might read, "The Colorado Avalanche pick up momentum!" What this means is that the team is sticking together and moving ahead as a whole rather than playing as individuals and not getting anywhere. In the engineering and physics world, momentum refers to the quality of motion that an object has, and it depends on the mass and velocity of the object:
Momentum = mass x velocity
So, if the Colorado Avalanche were all skating together in a close group at a fast speed, they would have a lot of momentum, physically.
Show the class a ping-pong ball and a golf ball. Although they are about the same size, the golf ball is heavier. Explain that if you threw each ball the same speed, the golf ball would have greater momentum. This becomes painfully obvious with an example. Ask the students if they have ever played "dodge ball" or a similar game. Ask the students if they would rather play with the ping-pong ball or the golf ball. As students groan at the thought of getting hit with a golf ball, explain that the reason it would hurt more is because it would have substantially more momentum than a ping-pong ball. In this case, more momentum is due to the greater mass (weight) of the golf ball, and the momentum of the golf ball would translate into a big bruise on your leg!
Lesson Background and Concepts for Teachers
A brief review of the concepts of potential and kinetic energy (covered in detail in the previous lesson) and momentum, is provided below:
Potential energy is the energy that an object has because of its position. Potential energy can also be thought of as stored energy — energy that an object has, as an inherent characteristic, but is not in use. It is sometimes called gravitational potential energy (PE). It can be expressed mathematically as follows:
PE = mass x g x height
where PE is the potential energy measured in Joules (J) and g is the acceleration due to gravity. At sea level g = 9.81 meters/sec2. An example of potential energy is a book resting on the edge of a table. If you were to nudge it off the edge of the table the book would fall to the floor and make a loud noise. This is an expression of kinetic energy. Kinetic energy is the energy an object has because of its motion; any object that is moving has kinetic energy. The falling book in this example is an illustration of kinetic energy. The kinetic energy depends on both mass and velocity and can be expressed mathematically as follows:
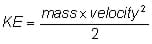
Momentum can be thought of as "mass in motion" and is given by the expression:
Momentum = mass x velocity
The amount of momentum an object has depends both on its mass and how fast it is going. For example, a heavier object going the same speed as a lighter object would have greater momentum. Sometimes, when objects collide into each other, momentum can be transferred from one object to another. There are two types of collisions that relate to momentum: elastic and inelastic. In a closed system, which means that there are no external forces acting on the objects that collide, both types of collisions follow the Law of Conservation of Momentum, which states "the total amount of momentum before a collision is equal to the total amount of momentum after a collision."

In an inelastic collision, momentum is conserved, but the total kinetic energy of the system is not conserved. When the collision occurs, some kinetic energy is transferred to another kind of energy such as heat or internal energy. A dropped ball of clay demonstrates an extremely inelastic collision. It does not bounce at all and loses its kinetic energy. Instead, all the energy goes into deforming the ball into a flat blob.
In the real world, there are no purely elastic or inelastic collisions. Even though rubber balls, pool balls (when hitting each other), and ping-pong balls may be assumed extremely elastic, there is still some bit of inelasticity in their collisions. If there were not, rubber balls would bounce forever. Refer to the Bouncing Balls: Collisions, Momentum & Math in Sports activity to have students investigate principle of conservation of momentum regarding elastic and inelastic collisions. For an extra challenge, refer to the Bouncing Balls: Collisions, Momentum & Math (for High School) activity. The degree to which something is elastic or inelastic is usually found experimentally.
The following demonstration shows momentum in action for an elastic collision. This demonstration is difficult to get right the first time, so practice a few times before presenting it to the class. First, bounce the ping-pong ball on the floor by dropping it from shoulder height. This works best on a tile floor. If your classroom is carpeted, bounce the balls onto a cinder block or a large brick placed on the carpet. Have a student volunteer mark on the board how high it bounced. Next, drop the golf ball from the same height and mark how high it bounced. Then, hold the golf ball and the ping-pong ball together, with the ping-pong ball directly on top of the golf ball. Drop them both and watch as the ping-pong ball bounces as high as 10 feet.
Another way to look to understand collisions is through Newton's 3rd Law, which tells us that "for every action, there is an equal and opposite reaction". When the golf ball hits the floor, the force exerted on the floor by the golf ball is equal and opposite to the force exerted on the golf ball by the floor. This causes the golf ball to bounce and move upwards. When the golf ball collides with the ping-pong ball, the force exerted on the ping-pong ball by the golf ball is equal and opposite to the force exerted on the golf ball by the ping-pong ball. As we know, the golf ball (due to its larger weight) has more momentum than the ping-pong ball, so it transfers momentum to the ping-pong ball, and so the ping-pong ball goes higher in this scenario than if it was dropped alone (no collision). Remember, based on the Law of Conservation of Momentum, after the collision between the golf ball and the ping-pong ball, the total momentum of the system is conserved. This means that if you added the momentum of the two balls before the collision and added the momentum of the two balls after the collision, the total would be the same.
Engineers consider momentum when designing vehicles for safety. In a head-on collision, the front end of a car is designed to crumple, making the collision inelastic. It takes energy to crumple the front of the car and this is what absorbs some of the impact. This makes the crash less severe for anyone that is in the car. Instead of absorbing the full force of the crash, the passengers are cushioned by the inelastic collision. (Note: This "cushion" is not as comfortable as a pillow, but it will save lives during accidents.)
Engineers also consider momentum when designing brakes for vehicles. Heavy trucks and race cars require powerful braking systems to stop. Have you ever wondered why drag racing cars have parachutes to stop them? It is because conventional brakes are not powerful enough to stop them in a limited distance. These cars go so fast that their momentum is too great for regular brakes to be sufficient.
Associated Activities
- Bouncing Balls: Collisions, Momentum & Math in Sports - To learn about the principle of conservation of momentum, students examine the elastic and inelastic collisions between three different types of balls.
- Bouncing Balls: Collisions, Momentum & Math (for High School) - In this activity, students examine how different balls react when colliding with different surfaces. They learn how to calculate momentum and understand the principle of conservation of momentum.
Lesson Closure
With the entire class, discuss why different sports use different balls. The students may have found that a golf ball has a more elastic collision than a baseball. This is because in a game, a golf ball must be hit a very long distance from the tee to the hole. On the other hand, if a baseball had a very elastic collision, almost every ball could be hit out of the park. That would not make for a very interesting game, would it? The choice of balls used in other sports can be explained with similar explanations.
Engineers address vehicular safety by studying collisions. The airbag is a recent safety addition to automobiles. If you tried to bounce an airbag do you think it would have a more elastic or inelastic collision? (Answer: Inelastic.) A similar effect can be seen in a ball of clay. Instead of bouncing, the energy is used up in deforming the clay (or airbag). A combination of characteristics makes an airbag a good safety device; using up energy to deform the bag instead of the driver's body is one of them. Other factors that help are distributing the force over a large area and time.
Vocabulary/Definitions
conservation of momentum: The amount of momentum in a system remains the same after a collision.
elastic collision: A collision in which all of the momentum is conserved. For example, a ball that bounces back up to its original height.
energy: The capacity to do work.
inelastic collision: A collision in which the kinetic energy is not conserved. For example, a ball that only bounces partially to its original height.
momentum: Mass in motion.
Assessment
Pre-Lesson Assessment
Voting: Ask the students to vote on the following question.
- Which has more momentum, a rolling bowling ball or ping-pong ball, going the same speed? (Answer: Bowling ball, because it has more mass.)
Brainstorming: In small groups, have the students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask the students:
- What factors determine how much momentum an object has? (Answer: Mass and velocity. Answers such as, size and density, or if an object is dropped, are acceptable answers because they can influence both mass and velocity.)
Post-Introduction Assessment
Discussion Question: Ask the students and discuss as a class:
- How could a ping-pong ball have enough momentum to stop a moving bowling ball? (Answer: If the ping-pong ball was going really, really fast.)
Lesson Summary Assessment
One and Done: Ask the students to think of a sport that involves a collision and transfer of momentum, and raise their hands (or indicate thumbs up) when they have an example. (Possible answers: Baseball, pool, bowling, football [i.e., field goal or punt, etc.]). Call on students at random to state their answer (the sport and description of the collision). Students put their hands down once they've contributed an answer. No repeat answers permitted.
Calculations: Ask students to complete the following calculations to test their new knowledge of momentum:
- Let's calculate the momentum of the golf ball in the above example. If the golf ball has a mass of .05 kg, and a velocity of 15 m/s, then what is its momentum? (Answer: momentum= .05 kg*15 m/s= 0.75 kg m/s)
- What if we were now dropping a rock instead? With a momentum of 220 kg m/s, and a velocity of 20 m/s, what is the mass of the rock? (Answer: m=momentum/velocity=220/20= 11 kg)
Toss-a-Question: Ask students to independently think of an answer to each of the questions below and write it on a half sheet of paper. Have students wad up and toss the paper to another team member who then adds their idea. After all students have written down ideas, have them toss the paper wad to another team, who reads the answers aloud to the class. Discuss answers with the class.
- How does the elasticity and inelasticity of balls affect sports?
- Why are baseballs not made out of super-elastic rubber? (Answer: If baseballs were made of rubber and were super-elastic, everyone could hit a home run easily.)
- Why are pool balls not made of clay? (Answer: If pool balls were made of clay it would be almost impossible to move the balls across the table.)
Lesson Extension Activities
Have the students further explore the mechanics of hitting a baseball with a bat by visiting this website: https://annex.exploratorium.edu/baseball/features/how-far-can-you-hit-one.html. This website covers the concept of momentum and collisions and how it relates to baseball in an easy-to-understand and interesting account of the mechanics of baseball. Visit the Exploratorium's baseball index at https://annex.exploratorium.edu/baseball/index.html for additional interesting science-based information on the game of baseball.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students examine how different balls react when colliding with different surfaces, giving plenty of opportunity for them to see the difference between elastic and inelastic collisions, learn how to calculate momentum, and understand the principle of conservation of momentum.

In this activity, students examine how different balls react when colliding with different surfaces. They learn how to calculate momentum and understand the principle of conservation of momentum.

Students also investigate the psychological phenomenon of momentum; they see how the "big mo" of the bandwagon effect contributes to the development of fads and manias, and how modern technology and mass media accelerate and intensify the effect.

On the topic of energy related to motion, this summary lesson ties together the concepts introduced in the previous four lessons and show how the concepts are interconnected in everyday applications. A hands-on activity demonstrates this idea and reinforces students' math skills in calculating energ...
References
Baseball highlights: http://memory.loc.gov/ammem/jrhtml/jr1947.html
Jacobs, Steve. Whelmer #22: Energy Transfer. Whelmers – McREL's Accessible Science Series, Mid-continent Research for Education and Learning. Accessed October 4, 2004. [Golf ball/ping pong ball energy transfer demo] http://www.mcrel.org/whelmers/whelm22.asp
Momentum: http://www.physicsclassroom.com/Class/momentum/index.cfm
Momentum and energy loss of balls colliding against different surfaces: http://www.iit.edu/~smile/ph8709.html.
The Exploratorium http://www.exploratorium.edu
Other Related Information
Browse the NGSS Engineering-aligned Physics Curriculum hub for additional Physics and Physical Science curriculum featuring Engineering.
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Bailey Jones; Matt Lundberg; Chris Yakacki; Malinda Schaefer Zarske; Denise CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: August 16, 2023









User Comments & Tips