Quick Look
Grade Level: 10 (9-12)
Time Required: 45 minutes
Expendable Cost/Group: US $1.00
Group Size: 3
Activity Dependency: None
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| HS-PS3-1 |
Summary
This activity shows students the engineering importance of understanding the laws of mechanical energy. More specifically, it demonstrates how potential energy can be converted to kinetic energy and back again. Given a pendulum height, students calculate and predict how fast the pendulum will swing by using the equations for potential and kinetic energy. The equations will be justified as students experimentally measure the speed of the pendulum and compare theory with reality.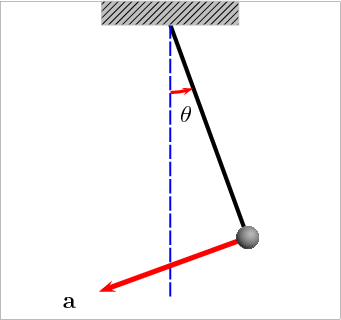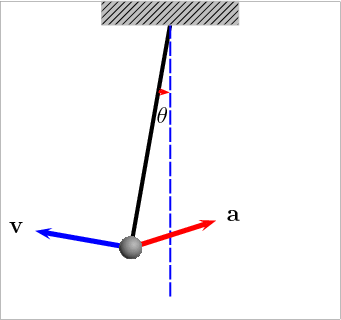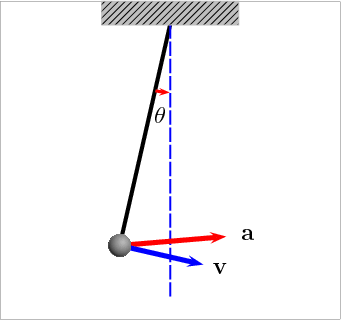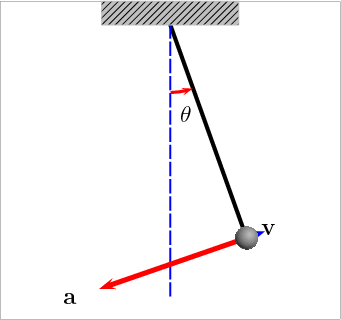
Engineering Connection
Mechanical engineers design a wide range of consumer and industry devices — transportation vehicles, home appliances, computer hardware, factory equipment — that use mechanical motion. The design of equipment for demolition purposes is another example. Similar to the movement of a pendulum, an enormous wrecking ball when held at a height possesses potential energy, and as it falls, its potential energy is converted to kinetic energy. As the wrecking ball makes contact with the structure to be destroyed, it transfers that energy to flatten or take down the structure.
Learning Objectives
After this activity, students should be able to:
- Understand the concepts of potential and kinetic energy.
- Relate concepts of kinetic and potential energy to real life examples, as well as to engineering examples.
- Understand that a pendulum has a specific period, regardless of where the weight on the pendulum is started, or how much it weighs.
- Use the concepts of kinetic energy, potential energy, and conservation of energy to perform an experiment to determine an object's velocity.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-1. Create a computational model to calculate the change in the energy of one component in a system when the change in energy of the other component(s) and energy flows in and out of the system are known. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Create a computational model or simulation of a phenomenon, designed device, process, or system. Alignment agreement: | Energy is a quantitative property of a system that depends on the motion and interactions of matter and radiation within that system. That there is a single quantity called energy is due to the fact that a system's total energy is conserved, even as, within the system, energy is continually transferred from one object to another and between its various possible forms. Alignment agreement: Conservation of energy means that the total change of energy in any system is always equal to the total energy transferred into or out of the system.Alignment agreement: Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Alignment agreement: Mathematical expressions, which quantify how the stored energy in a system depends on its configuration (e.g. relative positions of charged particles, compression of a spring) and how kinetic energy depends on mass and speed, allow the concept of conservation of energy to be used to predict and describe system behavior.Alignment agreement: The availability of energy limits what can occur in any system.Alignment agreement: | Models can be used to predict the behavior of a system, but these predictions have limited precision and reliability due to the assumptions and approximations inherent in models. Alignment agreement: Science assumes the universe is a vast single system in which basic laws are consistent.Alignment agreement: |
Common Core State Standards - Math
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve quadratic equations by inspection (e.g., for x² = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a ± bi for real numbers a and b.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy cannot be created nor destroyed; however, it can be converted from one form to another.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve quadratic equations by inspection, taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Use appropriate measurements, equations and graphs to gather, analyze, and interpret data on the quantity of energy in a system or an object
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Identify different energy forms, and calculate their amounts by measuring their defining characteristics
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Describe energy transformations both quantitatively and qualitatively
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 2 stopwatches (borrow from other teachers or ask students to bring a watch with a second hand from home)
- masking tape
- 10 feet of string or fishing line
- weight (to tie to string)
- calculator
- 3 copies of the Swinging Pendulum Worksheet
To share among groups:
- scale (optional, if mass of weight is unknown)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_energy_lesson03_activity2] to print or download.Introduction/Motivation
Remember that an object's potential energy (PE) is due to its position (height), and an object's kinetic energy (KE) is due to its motion (velocity). Potential energy can be converted to kinetic energy by allowing the object to fall (for example, a roller coaster going down a hill or a book falling off a table). This energy transformation also holds true for a pendulum, as illustrated in the diagram. As a pendulum swings, its potential energy converts to kinetic and back to potential, as illustrated in Figure 1.
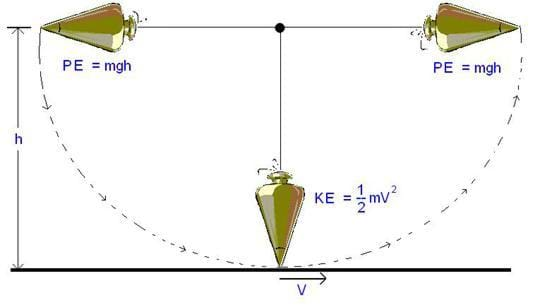
In this activity, students prove that the transformation of energy occurs by calculating the theoretical value of velocity at which a pendulum should swing and comparing it to a measured value. Students also compare the periods (the length of time it takes the pendulum to swing back and forth one time) of the pendulum by allowing it to swing from two different heights.
Four equations will be used in this activity:
PE = m∙g h
KE = ½ m∙Vt2
Vm = distance ÷ time
T = (2∙Π∙ ( l / g )½
where m is mass (kg), g is gravity (10 m/s2), h is height (meters), l is the length of the pendulum (m), Vt is the calculated velocity (m/s), and Vm is the measure velocity (also m/s), and T is the period of the pendulum(s). To make the calculations simpler, use the metric system for measurements and calculations.
Procedure
Before the Activity
- Gather materials.
- Designate several areas, depending on the size of your class, for pendulums to swing.
- Tie the string(s) or line(s) to the ceiling, leaving enough slack to reach the ground.
With the Students
Divide the class into groups of 3, and hand out the Swinging Pendulum Worksheet.
- Have each group measure and record the mass of the weight.
- Move each group to the designated test area and tie their weight to the line so that it barely misses the ground while hanging. The length of the pendulum will depend on the height of the ceilings in your classroom.
- Place two pieces of tape on opposite sides of the hanging pendulum so that their distances are 50 cm apart. The pendulum should rest in the middle of the two pieces of tape.
- Have students measure and record the height of the center of your weight when it is resting at equilibrium and again when it has swung to one of the pieces of tape.
- Students should calculate the potential energy of the weight when it reaches (swings to) the piece of tape. Each team member should do this, as a way to verify the result.
- Ask students to calculate the theoretical velocity, Vt, at the bottom of the swing by first calculating the kinetic energy of the weight at the bottom of the swing. (Note: Remind students to ignore wind resistance and other factors that would cause us to lose energy. Also, remind students to calculate the potential energy of the weight at equilibrium and factor this into their answer.)
- Instruct one or two students to pull back the weight until it reaches the edge of one of the pieces of tape.
- Have two students synchronize two stopwatches, each holding one, and start the stopwatches as soon as the weight is released.
- The first student should stop her/his stopwatch when the pendulum reaches the first piece of tape, and the second student should stop her/his watch when it reaches the second piece of tape (the original piece).
- Ask students to record the difference in times on their Swinging Pendulum Worksheet.
- Students should repeat the experiment three times.
- Repeat steps 4-12 but make set up the two pieces of tape so they are 80 cm apart.
- Instruct students to calculate the theoretical period of the pendulum.
- They should compare the theoretical period with their average measured period. (Note: The measured period is the time it takes for the weight to complete one full swing to one piece of tape and back to the other.)
- Instruct students to complete the Swinging Pendulum Worksheet.
Assessment
Pre-Activity Assessment
Question/Answer: Ask the students and discuss as a class:
- Where will the pendulum have the greatest amount of energy? (Answer: It has the same amount of energy wherever it is.)
Prediction: Ask the students to predict:
- Will a pendulum starting at a higher height go faster or slower than a pendulum that starts at a lower height? (Answer: It should go faster.)
- Will a pendulum starting at higher heights have a greater period? (Answer: It should be the same as a lower-starting pendulum no matter the height.)
Activity Embedded Assessment
- Complete the Swinging Pendulum Worksheet.
Post-Activity Assessment
Question/Answer: Ask the students and discuss as a class:
- If engineers can use potential energy (height) of an object to calculate how fast it will travel when falling, can they do the reverse and calculate how high something will rise if they know its kinetic energy (velocity)? (Answer: Yes, as long as you know either height or velocity, you can calculate the other.)
- For what might an engineer use this information? (Answer: To create other amusement park rides besides roller coasters, in racing, or how to launch something, etc.)
- Why did the pendulum have the same period even when the weight started from different heights? (Answer: The period of a pendulum is only dependent on the length of the pendulum, which is consistent no matter where the weight starts.)
Safety Issues
Make sure the students do not use the weighted pendulum to swing at (hit) one another.
Troubleshooting Tips
If students are complaining that the weight is not reaching the pieces of tape, ask them if they think it should and if so, why it is not. Then tell them to stop the stopwatches when the weight reaches the furthest point of its swing (right as the weight is changing direction).
If students have not had much experience with pendulums, then be sure to give them the equation for finding the period and help them with Question 5 from Calculations and Results section of the Swinging Pendulum Worksheet.
Activity Extensions
Pendulums can be used for many different tasks. Have your students research how pendulums are used today and specifically, how they are used by engineers.
Activity Scaling
- For all grades, if there is not enough time to complete the activity, have students complete the Swinging Pendulum Worksheet as homework.
- For lower grades, if students have never done any work with pendulums, then explain that this will be a good introduction to pendulums. Plan on working with them through the questions pertaining to the period of the pendulum and the pendulum itself.
- For higher grades, complete the activity as is.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

This activity demonstrates how potential energy (PE) can be converted to kinetic energy (KE) and back again. Given a pendulum height, students calculate and predict how fast the pendulum will swing by understanding conservation of energy and using the equations for PE and KE.

Students are introduced to both potential energy and kinetic energy as forms of mechanical energy. A hands-on activity demonstrates how potential energy can change into kinetic energy by swinging a pendulum, illustrating the concept of conservation of energy.

Using the LEGO® MINDSTORMS® kit, students construct experiments to measure the time it takes a free falling body to travel a specified distance. Students use the touch sensor, rotational sensor, and the brick to measure the time of flight for the falling object at different release heights.
Copyright
© 2006 by Regents of the University of Colorado.Contributors
Chris Yakacki; Malinda Schaefer Zarske; Denise Carlson; Janet YowellSupporting Program
Integrated Teaching and Learning Program and Laboratory, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: September 16, 2020








User Comments & Tips