Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $1.50
Group Size: 4
Activity Dependency: None
Associated Informal Learning Activity: Power, Work and the Water Wheel
Subject Areas: Physical Science, Science and Technology
NGSS Performance Expectations:

| MS-ETS1-2 |
| MS-PS3-5 |
Summary
Waterwheels are devices that generate power and do work. Student teams construct waterwheels using two-liter plastic bottles, dowel rods and index cards, and calculate the power created and work done by them.
Engineering Connection
Civil, geotechnical, environmental mechanical and electrical engineers collaborate to design and construct dams that generate electricity from the flow of water. When engineers design these dams, called hydroelectric power plants, they calculate the amount of power that can be generated by the plant. Knowing the dam's potential power generation, they can further estimate the maximum rural or urban region that can be supplied with electricity generated from the dam.
Learning Objectives
After this activity, students should be able to:
- Explain the connection between the concepts of power and work and engineering design.
- Work in a design group.
- Explain a nonlinear function (such as, power is inversely proportional to time).
- Collect data to solve equations and form conclusions.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ETS1-2. Evaluate competing design solutions using a systematic process to determine how well they meet the criteria and constraints of the problem. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Evaluate competing design solutions based on jointly developed and agreed-upon design criteria. Alignment agreement: | There are systematic processes for evaluating solutions with respect to how well they meet the criteria and constraints of a problem. Alignment agreement: | |
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS3-5. Construct, use, and present arguments to support the claim that when the kinetic energy of an object changes, energy is transferred to or from the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Construct, use, and present oral and written arguments supported by empirical evidence and scientific reasoning to support or refute an explanation or a model for a phenomenon. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | When the motion energy of an object changes, there is inevitably some other change in energy at the same time. Alignment agreement: | Energy may take different forms (e.g. energy in fields, thermal energy, energy of motion). Alignment agreement: |
Common Core State Standards - Math
-
Understand that rewriting an expression in different forms in a problem context can shed light on the problem and how the quantities in it are related.
(Grade
7)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy is the capacity to do work.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Power is the rate at which energy is converted from one form to another or transferred from one place to another, or the rate at which work is done.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Develop, communicate and justify an evidence-based scientific explanation to account for Earth's different climates
(Grade
8)
More Details
Do you agree with this alignment?
-
Examine, evaluate, and question information from a variety of sources and media to investigate how climates vary from one location to another on Earth
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 2-liter bottle with caps
- ¼-inch dowel rod (must be longer than the 2-liter bottle)
- 15 index cards
- 1.2 meters of string
- scissors
- tape
- 100-200 gram weight (about 1/3 pound)
- stopwatch or clock with a second hand
- kilogram or gram scale
- pitcher or water jug
- funnel
- water
- access to sink, outdoors or big bucket
- H2O Solutions Worksheet , one per person
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_energy_lesson02_activity1] to print or download.Introduction/Motivation
Power and work are important concepts that impact the engineering design of items ranging from racecar engines to elevators to power plants. High-power cars (high horsepower) are able to accelerate very quickly and go very fast. Elevators in skyscrapers require enough power to lift many people quickly. As we'll see, power plays an integral role in the production of hydroelectricity.
Work is measured in joules (J) and is defined as a force acting over a distance or:
work = force x distance
In our activity today, work will be done lifting a weight. The force term equals the weight and the distance term equals the height lifted. Power is measured in watts (W) and is defined by how fast work is done or:
power = work ÷ time
In this activity, you are working for H2O Solutions, an engineering design firm that works mostly with waterwheels and water energy! Your city wants to use hydropower instead of coal to make energy because they want to limit air pollution. The city has hired you to design an efficient watermill. The firm (our class) has been organized into several engineering teams (student groups). Each engineering team will design and test a slightly different design so that the firm can present the most efficient design to the city. You will calculate power and work by measuring force, distance and time for your team-built waterwheel.
Procedure
Before the Activity
- Gather materials and make copies of the H2O Solutions Worksheet, one per person.
- Drill 3/8-inch holes into the end of the two-liter bottle and the cap. This enables the bottles to spin symmetrically and freely about the dowel rod. (If you do not have the hole in the cap, the dowel rod will not spin symmetrically.)
With the Students
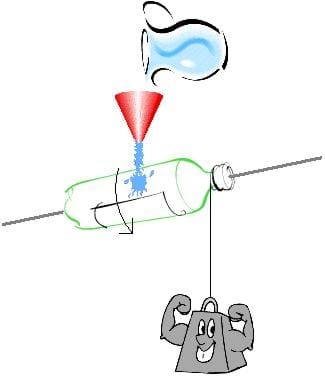
- Organize the students into groups of four and hand out the materials.
- Remind students of the context of the design challenge: They are engineers working for a firm hired to design an efficient waterwheel. Direct them to keep track of their design process using the worksheet.
- Direct groups to attach the index cards to the sides of the two-liter bottle to create waterwheels. (This task is open-ended, with details decided by each team.)
- Encourage groups to brainstorm different ideas of where to place the index cards.
- Explain that the water will be supplied from a pitcher through a funnel, causing the bottle to spin on the dowel rod.
- When teams are finished with their designs, have them tie the string to the cap end of the bottle so that when the bottle rotates, the string wraps around the bottle neck, pulling up the string.
- Measure and tie a weight to the other end of the string.
- Make sure to record the mass of the object in kilograms (kg). (For example, 100 grams is 0.1 kg.) Multiply the mass by gravity (~10) to calculate force.
- Have everyone use about the same amount of weight.
- Make sure the weights are not too heavy to lift. (For example, 100-200 gram weights work well.)
- Test the waterwheels by pouring water through a funnel to achieve an even flow and timing how long it takes to lift the weight 1 meter. (This is your distance.)
- Perform the tests outside or over a sink or big bucket.
- Have two students hold the ends of the dowel rod, one student pour the water and one student time how long it takes and write it down.
- Make sure the funnel is only a few inches above the waterwheel each time, and the same distance for each group.
- Have students calculate the work and power of their waterwheels.
- Work = force x distance
- Power = Work ÷ time
- Which team design had the most power? (Answer: They all do the same amount of work, but faster wheels have more power.)
Figure 2. Students test their waterwheels. Figure 3. Two girls hold their waterwheel design.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Write down all the groups' ideas on the board to share with the class.
- "What features make a good waterwheel?" (Example answers: A lot of fins/index cards to catch the water and turn the wheel/bottle, each fin/index card holds a large amount of water, symmetry, etc.)
Activity Embedded Assessment
Prediction: Have each engineering team predict how its waterwheel is going to perform and why. Based on their predictions, ask each group if its wheel will do more work or have more power than the other groups. (Answer: They all do the same amount of work, but faster wheels have more power.)
Post-Activity Assessment
Presentation: Have students present their designs to the other engineering teams in the firm (the class) to prepare for the presentation to the city. Students should explain why their design is the most efficient.
Question/Answer: Have students answer the following question in a short paragraph format. Review their answers to assess their depth of understanding.
- In your own words, explain the difference between work and power. (Answer: Work is a force acting over a distance and is measured in joules and not dependent on time. Power is work divided by time and is measured in watts.)
Question/Answer: Write the following problems on the classroom board (or overhead projector) and have students solve them. Review their answers to gauge their comprehension.
- Mr. Muscles loads up a bar with 910 newtons (≈205 lbs) of weight and pushes the bar up over his head eight times. Each time he lifts the weight .5 meters. How much work did he do? If he does the whole thing in 15 seconds, how much power did it take? (Answer: Work = 3640 joules. Power = 242.7 watts. Answer shown below.)
work = force x distance
force = 910 newtons
distance = .5 meters x 8 = 4 meters
work = 910 newtons x 4 meters = 3640 -ewton•meters = 3,640 joules
power = work ÷ time = 3,640 joules ÷ 15 sec = 242.7 joules/sec = 242.7 watts
- How long does it takes a swimmer with a power output of 275 watts to accomplish 3600 J of work?. If she applied a 650 N force during that time with the same power output, how far did she swim? (Answer shown below.)
- power = work / time --> time = work / power = 3600 J / 275 watts = 13.1 seconds.
- power = (force * distance) / time --> distance = (power * time) / force = (275 watts * 13.1 seconds) / 650 N = 5.54 meters)
Safety Issues
Make sure students are not reckless with the dowel rods.
If testing inside and on tile, the floor may be slippery when wet.
Troubleshooting Tips
If the weight is too heavy, the waterwheel may not work. If the weight is too light, you will not get accurate measurements of the waterwheel power.
Activity Extensions
Repeat the tests, but hold the funnel more than a few inches above the waterwheel. Does the power increase? (Answer: It should.) Ask students why they think this occurs. (Answer: The water has more potential energy at a higher height.)
Activity Scaling
- For lower grades, calculate work and power on the board as a classroom exercise.
- For upper grades, do multiple trials with different weights. The work done in each trial should be different but the power should stay the same. However, make sure the weights are not too heavy or too light.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

tudents create a model waterwheel and use it to calculate the amount of power produced and work done.

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

On the topic of energy related to motion, this summary lesson ties together the concepts introduced in the previous four lessons and show how the concepts are interconnected in everyday applications. A hands-on activity demonstrates this idea and reinforces students' math skills in calculating energ...

Students learn about the fundamental concepts important to fluid power, which includes both pneumatic (gas) and hydraulic (liquid) systems.
References
Kahan, Peter. Science Explorer: Motion, Forces, and Energy. Upper Saddle River, NJ: Prentice Hall, 2000.
Hazen, Theodor R. A Glossary of Water Wheel Terms. Pond Lily Mill Restorations. (definitions) http://www.angelfire.com/journal/millbuilder/terms.html
Lesson 1 - Basic Terminology and Concepts. Work, Energy and Power, Physics Tutorial. The Physics Classroom. Accessed 2005. http://www.physicsclassroom.com/Class/energy/index.cfm
Railroad Commission of Texas. http://www.rrc.state.tx.us
Water Wheel Factory. (Lots of photos of water wheels) http://www.waterwheelfactory.com
http://www.infinitepower.org/lessonplans.htm
Copyright
© 2004 by Regents of the University of ColoradoContributors
Bailey Jones; Matt Lundberg; Chris Yakacki; Malinda Schaefer Zarske; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under grants from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation (GK-12 grant no. 0338326). However, these contents do not necessarily represent the policies of the DOE or NSF, and you should not assume endorsement by the federal government.
Last modified: August 1, 2019









User Comments & Tips