Summary
Students learn what a pendulum is and how it works in the context of amusement park rides. While exploring the physics of pendulums, they are also introduced to Newton's first law of motion — about continuous motion and inertia.
Engineering Connection
Pendulums are used in many engineered objects, such as clocks, metronomes, amusement park rides and earthquake seismometers. In addition, engineers know that understanding the physics of how pendulums behave is an important step towards understanding motion, gravity, inertia and centripetal force. Engineers apply their understanding of these motion concepts to determine the force needed to propel an object into outer space, the braking power required to stop a vehicle at high speeds, and the optimal curve of a highway ramp. Teams of engineers work on a wide range of projects and solve problems that are important to society.
Learning Objectives
After this lesson, students should be able to:
- Describe how a simple pendulum moves.
- Relate pendulums to Newton's first law of motion.
- Explain several uses for pendulums in modern, everyday engineering applications.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
3-PS2-1. Plan and conduct an investigation to provide evidence of the effects of balanced and unbalanced forces on the motion of an object. (Grade 3) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Science investigations use a variety of methods, tools, and techniques. Alignment agreement: | Each force acts on one particular object and has both strength and a direction. An object at rest typically has multiple forces acting on it, but they add to give zero net force on the object. Forces that do not sum to zero can cause changes in the object's speed or direction of motion. (Boundary: Qualitative and conceptual, but not quantitative addition of forces are used at this level.) Alignment agreement: Objects in contact exert forces on each other.Alignment agreement: | A system can be described in terms of its components and their interactions. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
3-PS2-2. Make observations and/or measurements of an object's motion to provide evidence that a pattern can be used to predict future motion. (Grade 3) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Make observations and/or measurements to produce data to serve as the basis for evidence for an explanation of a phenomenon or test a design solution. Alignment agreement: Science findings are based on recognizing patterns.Alignment agreement: | The patterns of an object's motion in various situations can be observed and measured; when that past motion exhibits a regular pattern, future motion can be predicted from it. (Boundary: Technical terms, such as magnitude, velocity, momentum, and vector quantity, are not introduced at this level, but the concept that some quantities need both size and direction to be described is developed.) Alignment agreement: | Patterns can be used as evidence to support an explanation. Alignment agreement: |
Common Core State Standards - Math
-
Use appropriate tools strategically.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Generate measurement data by measuring lengths using rulers marked with halves and fourths of an inch. Show the data by making a line plot, where the horizontal scale is marked off in appropriate units— whole numbers, halves, or quarters.
(Grade
3)
More Details
Do you agree with this alignment?
-
Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
(Grade
4)
More Details
Do you agree with this alignment?
-
Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement:
(Grade
4)
More Details
Do you agree with this alignment?
-
Represent real world and mathematical problems by graphing points in the first quadrant of the coordinate plane, and interpret coordinate values of points in the context of the situation.
(Grade
5)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the role of society in the development and use of technology.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Explain how various relationships can exist between technology and engineering and other content areas.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Generate measurement data by measuring lengths using rulers marked with halves and fourths of an inch. Show the data by making a line plot, where the horizontal scale is marked off in appropriate units— whole numbers, halves, or quarters.
(Grade
3)
More Details
Do you agree with this alignment?
-
Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
(Grade
4)
More Details
Do you agree with this alignment?
-
Describe angles as geometric shapes that are formed wherever two rays share a common endpoint, and explain concepts of angle measurement.
(Grade
4)
More Details
Do you agree with this alignment?
-
Represent real world and mathematical problems by graphing points in the first quadrant of the coordinate plane, and interpret coordinate values of points in the context of the situation.
(Grade
5)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/cub_pend_lesson01] to print or download.Pre-Req Knowledge
A general understanding of the concepts of gravity and force.
Introduction/Motivation
Who has been on an amusement park ride called the Sea Dragon? Or, on a similar amusement park ride that looks like a big swinging ship? To get this ride started, a strong motor pushes the ship in an upward direction. Did you know that, after the ride is started, the motor does not need to do any more work, and the ride continues on its own? How do you think the ride stays in motion? Well, after the motor gives it an initial push, the ride uses inertia to keep moving. Inertia is the property of an object to stay moving unless it is stopped by an outside force.

Why doesn't the ride fly all the way around (360 degrees)? Well, gravity pulls the ride down when it gets high above the Earth. Even though the ride is pulled down by gravity, the inertia of the object pushes the ride right back up into the air, creating a swinging motion. Once the ride is in motion, it stays in motion unless an outside force slows it. At an amusement park, a ride like this is stopped by brakes, or else it would just keep swinging and you would be riding it long after closing time! To explain the amusement park ride the way we just did, we used the ideas of a pendulum and Newton's first law of motion.
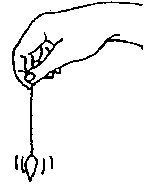
Who has heard of a pendulum before? A pendulum is made of an object with a mass, called a bob that dangles from the end of a rod or string and swings freely. The amusement park ride we just talked about is actually a huge pendulum. Can anyone think of another example of a pendulum? Anything that swings under its own weight is a pendulum — a playground swing, a curtain cord or a carpenter's plumb. Even your own legs behave like pendulums. In fact, the most efficient way to walk is to let your legs swing at their natural rate. The time it takes for your leg to make its back and forth movement depends on the length of your legs. That's why long-legged people sometimes appear to saunter along; short-legged people, to walk briskly. Some clocks, such as a grandfather clock, have a pendulum that swings to keep track of time. Because pendulums continue to swing without changing their speed unless acted on by an outside force, they can accurately help us measure things like time.
The type of pendulum we described with the Sea Dragon ride is known as a simple pendulum, because it only moves back and forth (like the swings on a playground swing set). Another type of pendulum is a spherical pendulum, in which the bob not only moves back and forth, but in a circular motion. Can anyone think of an example of a spherical pendulum? A tether ball moves as a spherical pendulum. Another example is an amusement park ride that spins you in a big circle.

Why does a pendulum stay in motion? More than 300 years ago, an Englishman named Isaac Newton described the natural behavior of motion and gravity in our world, in what he called the "three universal laws of motion." Newton's first law of motion says that an object in motion stays in motion and an object at rest stays at rest, unless acted upon by an outside force. So, something that is moving keeps moving until something else stops it. Does this remind you of the Sea Dragon ride? Or, have you ever been able to stop ice skating or roller skating without the help of an outside force (perhaps dragging your foot or crashing into someone)? Or, how do you stop when you are swinging on a playground swing?
Sometimes moving objects seem to stop without the help of an outside force. For example, if you slowly roll a ball across the floor, it eventually stops on its own. Does that mean Newton's first law of motion does not always hold true? No! The floor has roughness or friction — a resistance to motion — that slows the ball. In this case, friction is the outside force that stops the ball from rolling. Pendulums work so well because they move through air, which has very little friction.
Engineers often incorporate the ideas of the pendulum and Newton's first law of motion when they design things that we use everyday or that help people in some way. In fact, engineers always must consider the "invisible" natural forces acting on objects in motion, such as inertia, to keep us safe. What are some ways that an engineer might be able to use a pendulum?

Engineers use pendulums in designing lots of things, from clocks to amusement park rides. Some engineers who study the Earth and earthquakes, design equipment and sensors such as seismometers, which use the idea of a pendulum to measure earthquakes. Understanding pendulum mathematics helps engineers determine how much swaying back and forth a building can safely withstand during a windstorm or earthquake. If a building might build up too much inertia moving it back and forth, then engineers must figure out ways to safely counteract the movement to protect the people and property. Real-world applications like these make the pendulum and inertia important concepts for engineers — and you — to understand. To help convey the lesson's content, refer to the associated activity Swinging with Style where students experientially learn about the characteristics of pendulums by riding on playground swings.
Lesson Background and Concepts for Teachers
Newton's First Law of Motion
Newton's three laws of motion make up the foundation for the known physics of motion. The first law states that an object in motion stays in motion and an object at rest stays at rest, unless acted upon by an outside force. This is the concept of inertia. For example, a book falls until it hits a table, and then the book stops falling because an outside force stopped it from its original path of motion.
Gravity
One of the greatest forces acting on our planet is the force of gravity. This is the force that holds objects down to the Earth, keeping them from flying off into space. In the case of a pendulum, gravity is the force pulling the mass down, while inertia is the property keeping the mass in motion and pulling it back up. When sitting on a swing, the swing does not move until you are pushed or you pump your legs, creating the force that sets you in motion. But, you continue swinging, without extra pumping, until the friction of the air and the swing chain resist the motion. Gravity pulls you down, and inertia keeps you moving (until friction intervenes)b
Mathematics of a Pendulum Swing
The motion of a pendulum was first mathematically described by the Italian Galileo Galilei in the late 1500s. Galileo also investigated how things fall, how planets move, and many other natural scientific phenomena. Many of his discoveries grew out of his observations of how a pendulum swings.
As explained by Galileo, we know that the period of a pendulum can be described mathematically by the following equation:
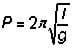
Where:
P = period; which is the time for one pendulum swing [sec]
l = length from the fixed point at the top of the pendulum to the center of mass of the bob [m]
g = gravitational constant (9.8 m per sec2)
π ≈ 3.14 (dimensionless constant)
Note that this equation does not include terms for the mass of the pendulum or the angle it swings through. The only factor that significantly affects the swing of a pendulum on Earth is the length of its string.
For more about the mathematics behind the swing of a pendulum, see the sixth-grade TeachEngineering Swinging on a String lesson.
Associated Activities
- Swinging with Style - Students experientially learn about the characteristics of pendulums by riding on playground swings. They use pendulum terms and a timer to experiment with swing variables. They use their measurements and follow the steps of the engineering design process to design timekeeping devices powered by human swinging.
Lesson Closure
Now that we've learned all about pendulums and Newton's first law of motion, can you explain how the Sea Dragon or big boat swing amusement park ride works? Remember, a pendulum is made of an object with a bob that dangles from the end of a rod or string and swings freely. Newton's first law tells us that an object at rest stays at rest (without outside interference), so a motor must first push the amusement park ride up into the air. Then gravity pulls the ride back down. The ride has inertia, which keeps it in motion. The ride moves up and down with the help of inertia and gravity. The only thing that can stop the ride is friction, which is supplied from the brakes.
Would you want to design an amusement park ride? What ideas do you have? How else do engineers use the ideas they get from pendulums and Newton's first law of motion? Engineers incorporate pendulums in many projects — such as designing clocks, designing amusement park rides, studying the Earth and earthquakes with seismometers, and determining how much swaying movement a structure or tower can safely withstand during storms.
Now that you know how a pendulum works, if you can convince the amusement park ride operator not to use the brakes, you could stay on the amusement park ride for even longer!
Vocabulary/Definitions
bob: The weight at the end of the string or rod of a pendulum.
engineer: A person who applies their understanding of science and math to creating things for the benefit of humanity and our world.
engineering: Creating things for the benefit of humanity and our world.
friction: A resistance to motion.
gravity: The Earth's force that pulls everything downward.
inertia: The property of an object to stay moving unless it is stopped by an outside force.
Newton's first law of motion: An object in motion stays in motion and an object at rest stays at rest, unless acted upon by an outside force
pendulum: An object attached to a fixed point by a string or rod so that it can swing freely under the influence of gravity and acquired momentum. Often used to regulate devices, such as clocks.
simple pendulum: A pendulum that swings back and forth.
spherical pendulum: A pendulum that swings in a circular motion.
Assessment
Pre-Lesson Assessment

Demonstration/Discussion: Tie a tennis ball (or other soft ball or weight) to the ceiling of the classroom, and use it to demonstrate the following pendulum scenarios to the students. Point out the characteristics of a pendulum, and have them think about why pendulums behave the way that they do. Engage the class in open discussion, respectfully listening to all ideas.
- Pull back the tennis ball and let go, so it swings back and forth. After a period of observation, ask the students to suggest their ideas on what makes the ball keep moving for so long. (Encourage all ideas at this stage, as they will learn the answers during the lesson.)
- Swing the tennis ball around in a circular motion. Ask the students what the differences are between the two demonstrations. (Answer: In the first demonstration, the ball only moves back and forth, and in the second one, it moves in a circular motion.)
- Have students discuss any patterns that can be used to describe future motion.
Post-Introduction Assessment
On-Playground Demo/Discussion: While at the playground swings (or using another pendulum) hold one swing and chain (pendulum bob) taught towards a stationary object, such as a chair (or trash can or very still brave person). Ask students to watch carefully. Then release the swing (pendulum). Ask the students:
- Why does the bob not hit the object? (Answer: A pendulum can never swing higher than its starting point; gravity pulls the bob down. You may want to do this a few more times so students can be convinced that this is true. Is anyone brave enough to hold the swing up to their nose and stay there, knowing the swing will not hit them in the nose? If you do this, be careful to just release the pendulum; if you push it [add energy], it will come back to its original position and perhaps break your nose.)
- What keeps the bob moving? (Answer: Inertia is the property that keeps an object in motion until it is stopped by an outside force.)
- Is the Sea Dragon amusement park ride we described a simple pendulum or spherical pendulum? (Answer: It is a simple pendulum because it only moves back and forth.)
After-Playground Math Practice: Have the students fill out the attached Graphing Worksheet and discuss how string length and start angle affect the speed at which the pendulum swings!
Lesson Summary Assessment
Amusement Park Engineering: What are some pendulums that engineers help to design? (Amusement park rides, clocks, earthquake seismometers, etc.) Have students design a new amusement park ride in which a pendulum is used. Have them name their ride and explain how it works, using the terms pendulum and inertia. Remind students that amusement park rides are designed by engineers who have learned about laws of motion. Places like Disneyland and Six Flags employ engineers to help them design their new attractions.
Lesson Extension Activities
Pendulum Scavenger Hunt: Ask students to look for simple pendulums on their way home and at home. They might find them in places that they did not think of before! Perhaps a hallway or dining room light fixture support. Even swinging a set of keys around your finger might be considered a pendulum.
Sand Pendulum: Make a cone-shaped cup and fill it with sand or salt. Swing the cone like a pendulum, letting the sand pour out from a hole in the bottom of the cone. Observe the pattern it makes.
Pendulums in Space: Have students think about how pendulums would behave on different planets. If you traveled to another planet, you could use a pendulum's length and period to determine the planet's gravitational pull. On our Moon, a pendulum's period would be longer than its period on Earth. That's because gravity on the Moon is only one-sixth as strong as gravity on Earth.
Additional Multimedia Support
Amusement Park Physics – Pendulum. Annenberg Media. Accessed December 12, 2022. http://www.learner.org/exhibits/parkphysics/pendulum.html
Amusement Park Physics: What are the forces behind the fun? Annenberg Media. Accessed December 12, 2022. https://www.learner.org/series/interactive-amusement-park-physics/
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students experientially learn about the characteristics of a simple physics phenomenon — the pendulum — by riding on playground swings. They use pendulum terms and a timer to experiment with swing variables. They extend their knowledge by following the steps of the engineering design process to desi...

Students explore how pendulums work and why they are useful in everyday applications. In a hands-on activity, they experiment with string length, pendulum weight and angle of release.
References
Baine, Celeste. The Fantastical Engineer: A Thrillseeker's Guide to Careers in Theme Park Engineering. Second edition. Trade Paperback, published May 2007. Source: http://engineeringedu.com/store/fantastical.html
Dictionary.com. Lexico Publishing Group, LLC. Accessed July 17, 2007. (Source of some vocabulary definitions, with some adaptation) http://www.dictionary.com
Pendulum Table Floor Exhibit. 1995. Exploratorium Exhibit & Phenomena Cross-Reference, Digital Library Learning Resources Collection, San Francisco, CA. Accessed July 18, 2007. (ITL Laboratory, University of Colorado at Boulder exhibit installation) http://www.exploratorium.edu/xref/exhibits/pendulum_table.html
Copyright
© 2007 by Regents of the University of Colorado.Contributors
Ashleigh Bailey; Megan Podlogar; Malinda S. Zarske; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.
Last modified: October 9, 2024





User Comments & Tips