Lesson Processes on Complex Networks

Learning Objectives

After this lesson, students should be able to:

• Identify processes as being non-random and random.
• Model the spread of an infectious disease, such as the flu, on a given social network by flipping a coin.
• Generally explain how scientists and engineers use mathematics to model and simulate random processes on complex networks.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

International Technology and Engineering Educators Association - Technology

State Standards

Pre-Req Knowledge

An understanding of how graphs are used to represent complex networks, as introduced in the Complex Networks and Graphs lesson and its associated activity.

Introduction/Motivation

Imagine these scenarios: Infectious diseases spreading among people in a social network. Life being maintained by the ebb and flow of biochemical species through reaction networks in individual cells. Human thoughts arising in the brain due to complex firing patterns of neurons in complex neural networks. In complex networks like these, scientists and engineers apply the mathematics of random processes on networks to study these important problems and develop sophisticated analysis techniques.

What is a process? In mathematics, this terminology refers to a variable whose value changes over time. Let's see what this means.

Can anyone think of a variable that changes over time? (Listen to student ideas; there are many possible answers. As necessary, share these examples: the number of students attending a class, the number of phone calls or text messages received by a student during a given day, the number of students waiting in the cafeteria line to be served.)

Good, so we understand what it means to have a variable that changes over time. Mathematically, we represent this by having the variable be a function of time. For example, if X is our variable, then we write X(t) to denote the fact that the value of variable X depends on time t. For example, if X denotes the number of students in a class, then X(8) may refer to the number of students in the class at 8am, whereas, X(10) may refer to the number of students in the class at 10am. Various reasons might explain how these two numbers might not be the same. For example, there may be 25 students attending the class at 8am, in which case, X(8) = 25, whereas, the class may have ended by 10am, in which case X(10) = 0.

A process X(t) is random whenever there is no way to predict exactly the value of variable X at time t. For example, if the number of students attending a class is always the same, say 25, and if the class starts and ends at the same time every day, then we can determine the value of X(t) at any time t. In particular, X(t) = 25 when the class is in session and X(t) = 0 at all other times. However, this is not always the case.

To understand why, let us consider the case when X(t) is the number of students waiting in a cafeteria line at time t. In general, we are not able to predict the value of X(t) (although this number will be zero when the cafeteria is closed), since students usually arrive at the cafeteria and get served at random times. For example, a student does not arrive at the cafeteria at the exact same time every day, since one day he might stop to tie his shoe or the next day class might get out slightly earlier than usual.

Let's talk this through. Say that at noon 60 students are waiting in line to be served by the school staff. How many students will be in line one minute later? At 12:01 there might be still 60 students waiting in line, if no student is served and no new student arrives, or one student is served and one new student arrives, and so on. On the other hand, there might be 59 students waiting in line, if a student is served and no new student arrives, or two students are served and a new student arrives, and so on. Since we do not know what exactly will happen between 12:00 and 12:01, we cannot determine the number of students waiting in line at 12:01.

(Verify that students understand the concept of a random process by conducting Assessment 1: Random Processes, as described in the Assessment section.)

Next, let's discuss random processes on networks. Specifically, we will examine how a flu epidemic, or a similar infectious disease, spreads on a social network of students. (Continue on to present to students the content on graphs and modeling disease spread [via the SIR model] covered in the Background section, and the associated assessment.) Following the lesson, conduct the associated activity Curb the Epidemic! for a student led investigation using a website simulation tool to interact with the graph of a social network and simulate the spread of a disease. 

Lesson Background and Concepts for Teachers

Review of Graphs

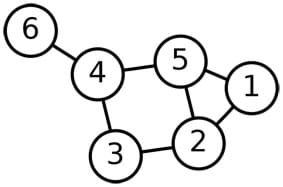
First, we must represent the social network of students by a graph (as learned in the associated Sets-Nodes-Edges: Representing Complex Networks in Graph Theory lesson). (Draw the Figure 1 graph on the classroom board.) How could this graph represent potentially infectious contacts between students? (Listen to student explanations.) The nodes N = {1, 2, 3, 4, 5, 6} represent six students. The edges between these nodes represent potentially infectious contacts. For example, since {1, 2} is an edge, we expect that student 1 and student 2 have the potential to infect each other with the flu (for example, perhaps they attend the same homeroom in the mornings). Note also that node 1 is not connected to node 6 by an edge, which means that student 1 never comes into infectious contact with student 6.

Modeling Disease Spread

Next, let's discuss how to model a flu infection. The most common way to do so is by a model known as the SIR model, in which students at each node of the graph can exist in one of three states with respect to an infection: susceptible (S) to becoming infected, infectious (I), or resistant (R) to becoming infected. A student in state S can change to state I; this may occur when the student comes in contact with an infectious student. Of course, for this to happen, the two students must have an edge connecting them on the graph. On the other hand, a student at state I can move to state R, since once a student recovers from the flu, she can never be infected again by that same flu strain.

Now, let X₁(t) represent the state of student 1 at time t [that is, X₁(t) = S, if student 1 is susceptible at time t, X₁(t) = I, if student 1 is infectious at time t, and X₁(t) = R, if student 1 is resistant at time t]. Likewise, X₂(t) is the state of student 2, and so on for X₃(t), X₄(t), X₅(t), and X₆(t). Specifying the values of all variables X at time t results in specifying the state of the social network at time t, which tells us everything about the status of flu infection at time t. For example, if t = 0 is the start of the school day and

X₁ (0) = I, X₂ (0) = S, X₃ (0) = R, X₄ (0) = S, X₅ (0) = R, X₆ (0) = S

then we can say that, at the start of the day, there are three susceptible students (students 2, 4 and 6), one infectious student (student 1) and two resistant students (students 3 and 5).

To make our life easier, let's assume at this point that we are only interested in the state of the social network at discrete time points, such as t = 1, 2, 3, etc. To model how the flu spreads from time t to the next time of interest t+1, we must specify the states X₁ (t+1), X ₂(t+1), X ₃(t+1), X₄ (t+1), X₅ (t+1), X₆ (t+1) from our knowledge of the states at time t. However, this cannot be done exactly, since we do not know whether or not a particular susceptible student will be infected with flu and whether or not a particular infected student will recover from the flu within the time from t to t+1. In other words, the states X ₁(t+1), X ₂(t+1), X ₃(t+1), X ₄(t+1), X₅(t+1), X ₆(t+1) are random.

To proceed, we will make assumptions about how the infection spreads. A susceptible student at time t can be infected at the next time t +1 if she is in contact with (that is, connected on the graph with) a student who is infectious at time t. Infection does not always happen after contact. So since we do not know whether or not an infection occurs after contact, we must assume that infection happens randomly. In particular, we will say that it happens with some probability, say 0.5 (a probability of zero means infection will never occur, whereas, a probability of 1 indicates that infection will always occur after contact). In this case, we can decide whether or not a susceptible student becomes infected or not by flipping a coin. If the result of flipping is HEADS, then we can decide that this contact infects the susceptible student. If the result of flipping is TAILS, then we can decide that this contact does not infect the susceptible student. We can do this because the probability of getting HEADS by flipping a (fair) coin is 0.5, whereas, the probability of getting TAILS is also 0.5. Likewise, we will also assume that an infected student at time t will recover at time t +1 and become resistant to the flu with some probability, say 0.5.

By using the previous assumptions, we are now ready to explain how the flu will spread on the social network. At time t = 0, we can start the system by assuming that only one student (say, student 1) is infectious, whereas, all other students are susceptible to the flu. In this case, the state of the social network at time t = 0 is given by:

X₁ (0) = I, X₂ (0) = S, X₃ (0) = S, X₄ (0) = S, X₅ (0) = S, X₆ (0) = S

According to the Figure 1 graph, student 1 can get in contact with students 2 and 5. Student 2 is susceptible to the flu and is connected to (the infectious) student 1 on the graph. So, with 0.5 probability, student 2 can become infected at time t = 1. To see what will happen, we flip a coin and observe the outcome, which turns out to be HEADS. In this case, student 2 will be infected at time t = 1. We follow the same procedure for student 5, but this time coin flipping results in TAILS. This tells us that student 5 will not get infected by student 1. We finally see that student 1 can recover at time t = 1 and become resistant. To see what will happen, we flip again and observe the outcome, which turns out to be HEADS. In this case, student 1 will be recovered from the flu at time t = 1. As a consequence, the state of the social network at time t = 1 is given by:

X₁ (1) = R, X₂ (1) = I, X₃ (1) = S, X₄ (1) = S, X₅ (1) = S, X₆ (1) = S

Now, student 2 is infectious. According to the Figure 1 graph, this student can only get in contact with students 1, 3 and 5. Student 2 cannot infect student 1, since this student is resistant to the flu. However, student 2 can infect students 3 and 5, since both of these students are susceptible to the flu. To see what will happen at time t = 2, we flip the coin for student 3 and observe the outcome, which turns out to be TAILS. In this case, student 3 will not get infected by the flu. Likewise, we flip the coin for student 5 and we find out that the student will not get infected at time t = 2 (what is the outcome of flipping the coin in this case?). Finally, by flipping the coin once more we obtain HEADS, which means that student 2 recovers at time t = 2 and becomes resistant to flu infection. As a consequence, the state of the social network at time t = 2 is given by:

X₁ (2) = R, X₂ (2) = R, X₃ (2) = S, X₄ (2) = S, X₅ (2) = S, X₆ (2) = S

Note now that there are no infectious students anymore. For this reason, students 3, 4, 5 and 6 cannot get infected. As a consequence, the state of the social network will not change at subsequent times. If we repeated the previous procedure once more from the beginning, what would be the result? (Listen to student answers.) We may get a different result due to randomness. For example, if nothing changed except for the fact that the coin flip for student 2 at time t = 1 produces TAILS instead of HEADS, then student 2 will not recover at time t = 2, in which case, the state of the social network at time t = 2 would be given by:

X₁ (2) = R, X₂ (2) = I, X₃ (2) = S, X₄ (2) = S, X₅ (2) = S, X₆ (2) = S

This opens the possibility of a state change at time t = 3, since an infectious student is now in the network.

Unfortunately, as you have just seen, it is difficult and time consuming to follow the previous steps using only paper and pencil. This is especially true when we are dealing with large social networks with many students. For this reason, network engineers use computers because they can run thousands or millions of calculations, such as the ones we just went through, which can then be used to simulate how diseases spread on social networks. This is true for other types of complex networks as well. From these simulations, scientists and engineers can answer some important questions. For example, what is the average time at which all students in the network recover from the flu?

(To conclude, verify that students understand how diseases spread on complex networks by conducting Assessment 2: Disease Spread, as described in the Assessment section.)

Associated Activities

• Curb the Epidemic! - Using a website simulation tool, students interact with a social network model and simulate the spread of a disease. They input certain parameters describing the population and rate of vaccination, aiming to minimize the number of people infected. They see the random process on networks in action while running multiple simulations, then analyze the results and assess the effectiveness of their vaccination strategies.

  Watch this activity on YouTube

Lesson Closure

In this lesson, you have learned about random processes on networks. As an example, we focused on how the flu can propagate on a social network of students interacting with each another. The calculations involved are often very time consuming or impossible to do with just a piece of paper and a pencil. That's why network researchers and engineers use computers to perform these calculations and study how diseases spread on social networks.

Vocabulary/Definitions

infectious : A student capable of spreading a disease.

probability: A number (between 0 and 1) that tells us how probable the occurrence of an event is, with 0 meaning that the event cannot happen and 1 meaning that the event always happens.

process: A variable that changes with time.

random process : A variable that changes with time, but cannot be completely predicted.

resistant: A student who is immune to future infections of the same disease.

simulation: A calculation of a process using computers.

SIR model: A mathematical model of disease spreading over social networks.

susceptible: A student capable of becoming infected by a disease.

Assessment

Assessment 1: Random Processes (before moving to processes on graphs)

Verify that students understand the concept of a random process by asking them to classify each of the following examples as a non-random process, a random process, or neither:

• The position of the Earth in orbit around the Sun. (Answer: This is a non-random process. According to Newton's laws of motion, the Earth follows a completely predictable orbit around the Sun.)
• The speed and direction of the wind outside the classroom. (Answer: This is a random process. Although a weather forecast might predict an approximate wind speed and direction, both change erratically and unpredictably at any given time and location. Just watch a flag on a flagpole moving in the wind.)
• Your age. (Answer: This is a non-random process. You know how your age changes with time. One year from today, you will be one year older.)
• The weight of your desk. (Answer: This is not a process of any type. The weight of the desk does not change over time [if we ignore degradation after many years].)

Assessment 2: Disease Spread (at lesson end)

Verify that students understand how diseases spread on complex networks by presenting them with the following problem. Consider a network represented by the Figure 1 graph, with initial state:

X₁ (0) = I, X₂ (0) = S, X₃ (0) = S, X₄ (0) = S, X₅ (0) = S, X₆ (0) = S

To minimize the spread of the disease, choose any two susceptible students on the network and make them resistant to the flu by vaccinating them. To which students should you give these vaccines? (Answer: To make sure that the flu will never spread, vaccinate students 2 and 5 since the one infectious individual can be in contact only with these two students who have both become resistant to a flu infection by vaccination.)

References

Copyright

Contributors

Supporting Program

Acknowledgements

The generous support of the National Science Foundation, Directorate for Computer and Information Science and Engineering (CISE), Division of Computing and Communication Foundations (CCF), is gratefully acknowledged.