Summary
After watching a 1940 film clip of the "Galloping Gertie" bridge collapse and a teacher demo with a simple pendulum, student groups discuss and then research the idea of motion that repeats itself—specifically the concepts of periodic and harmonic motion. They become aware of where and how these types of motion occur and affect them in everyday applications, both natural (seasons, tides, waves) and engineered (swings, clocks, mechanical systems). They learn the basic properties of this type of motion (period, amplitude, frequency) and how the rearrangement of the simple pendulum equation can be used to solve for gravitational acceleration, pendulum length and gravity. At lesson end, students are ready to conduct the associated activity during which they conduct experiments that utilize swinging Android® devices as pendulums.Engineering Connection
Engineers are constantly exploiting the periodic nature of systems for technological use and ways to improve our lives. Mechanical engineers design machines that have periodic features. Music is created by manipulating sound waves, which are periodic. Manipulating both sound and electromagnetic waves creates communication. When engineers design bridges that span distances, the forces acting on the span must be considered so that periodic motion does not develop and cause structural failure. Periodic motion can be both helpful and harmful, depending on the situation.
Learning Objectives
After this lesson, students should be able to:
- List the properties of harmonic motion.
- Cite real-world examples of periodic motion.
- Explain how engineers utilize or harness periodic motion.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS4-1. Use mathematical representations to support a claim regarding relationships among the frequency, wavelength, and speed of waves traveling in various media. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use mathematical representations of phenomena or design solutions to describe and/or support claims and/or explanations. Alignment agreement: | The wavelength and frequency of a wave are related to one another by the speed of travel of the wave, which depends on the type of wave and the medium through which it is passing. Alignment agreement: | Empirical evidence is required to differentiate between cause and correlation and make claims about specific causes and effects. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS4-5. Communicate technical information about how some technological devices use the principles of wave behavior and wave interactions with matter to transmit and capture information and energy. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Communicate technical information or ideas (e.g. about phenomena and/or the process of development and the design and performance of a proposed process or system) in multiple formats (including orally, graphically, textually, and mathematically). Alignment agreement: | Solar cells are human-made devices that likewise capture the sun's energy and produce electrical energy. Alignment agreement: Information can be digitized (e.g., a picture stored as the values of an array of pixels); in this form, it can be stored reliably in computer memory and sent over long distances as a series of wave pulses.Alignment agreement: Photoelectric materials emit electrons when they absorb light of a high-enough frequency.Alignment agreement: Multiple technologies based on the understanding of waves and their interactions with matter are part of everyday experiences in the modern world (e.g., medical imaging, communications, scanners) and in scientific research. They are essential tools for producing, transmitting, and capturing signals and for storing and interpreting the information contained in them.Alignment agreement: | Systems can be designed to cause a desired effect. Alignment agreement: Science and engineering complement each other in the cycle known as research and development (R&D).Alignment agreement: Modern civilization depends on major technological systems.Alignment agreement: |
Common Core State Standards - Math
-
Interpret functions that arise in applications in terms of the context
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Synthesize data and analyze trends to make decisions about technological products, systems, or processes.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Council of Teachers of Mathematics - Math
-
recognize and apply mathematics in contexts outside of mathematics
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
understand relations and functions and select, convert flexibly among, and use various representations for them
(Grades
9 -
12)
More Details
Do you agree with this alignment?
National Science Education Standards - Science
-
Use technology and mathematics to improve investigations and communications. A variety of technologies, such as hand tools, measuring instruments, and calculators, should be an integral component of scientific investigations. The use of computers for the collection, analysis, and display of data is also a part of this standard. Mathematics plays an essential role in all aspects of an inquiry. For example, measurement is used for posing questions, formulas are used for developing explanations, and charts and graphs are used for communicating results.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Mathematics is essential in scientific inquiry. Mathematical tools and models guide and improve the posing of questions, gathering data, constructing explanations and communicating results.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Scientists rely on technology to enhance the gathering and manipulation of data. New techniques and tools provide new evidence to guide inquiry and new methods to gather data, thereby contributing to the advance of science. The accuracy and precision of the data, and therefore the quality of the exploration, depends on the technology used.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Nebraska - Science
-
Describe motion with respect to displacement and acceleration
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Introduction/Motivation
(Be ready to show students a six-minute online video. For a class demonstration, have handy a simple pendulum, such as a ball on a string, to which you are able to vary the length, angle and weight. Also be ready to provide student groups with access to computers with Internet connections for online research.)
In this lesson, you will learn about harmonic motion and its components. Harmonic motion is all around you in the world. It is in the rhythms of nature, how the universe moves, and the mechanical systems that engineers create. Sometimes harmonic motion can cause problems. One famous example is the Tacoma Narrows Bridge, nicknamed "Galloping Gertie." The bridge was designed by structural engineers who did not adequately take into account the role of harmonic motion. Watch this video to see what happened: https://www.youtube.com/watch?v=j-zczJXSxnw.
(After the video, show students a simple pendulum, such as a ball on a string. Demonstrate the motion of the pendulum.) What do you notice about the pendulum and its motion? (As students observe the pendulum, vary different parameters such as length, angle, weight, etc.) How does each change affect the motion of the pendulum?
Next, you will work in groups with the following task: To discuss motion that repeats itself. Think about day/night, clocks, swings, etc. After doing this for a brief time, do some Internet research on the topic of harmonic or periodic motion. What are some examples? How have engineers harnessed this type of motion? What problems can it cause? (Divide the class into small groups and give them time to discuss the topic and conduct some Internet research.) Remember to take notes on what you learn.
(After the allotted time for research and exploration, bring the class together for a discussion to establish a working knowledge of periodic motion. Ask students some questions, such as the following, at a minimum, and get them talking to share what they learned from their research.)
- What are some instances of periodic motion in your daily lives? (Possible answers: The seasons, grandfather clocks, playground equipment, tides, vibrating instrument strings, any wave, etc.)
- How can you affect the motion of a pendulum? (Answer: Change its length; change its angle.)
- What are some basic properties of periodic motion? (Answer: The distance it moves [amplitude]; the time for it to go back to start [period]; the number of cycles for a given time unit [frequency].)
- What is period? (Answer: The amount of time it takes for an object experiencing periodic motion to complete one full cycle and return to the same relative position.)
- What is amplitude? (Answer: A periodic variable that is a measure of change over a single period. Typically, it is measured from an object's equilibrium point to its most extreme value.)
- What is frequency? (Answer: The number of occurrences of a repeating event per unit time.)
- How do engineers exploit periodic motion? (Example answers: The movement in mechanical systems are often repeated [period motion]. Sound and electromagnetic waves serve as communication, etc.)
(Continue by delivering the content in the Lesson Background section.)
Lesson Background and Concepts for Teachers
The information below describes how pendulums move, as considered from several different frameworks. To prepare students to conduct the associated activity Android Pendulums, during which they explore periodic motion by using pendulums, discuss all the different frameworks to make sure they fully understand pendulum motion.
Various Definitions of the Motion of a Simple Pendulum 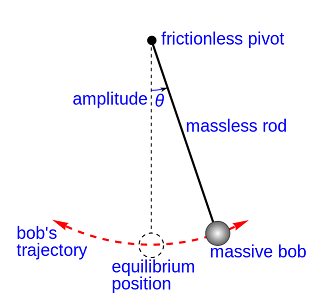
- In recognizable terms: The motion of a simple pendulum is periodic motion, harmonic motion, oscillation, vibration.
- In conceptual terms: The motion of a simple pendulum is a harmonic motion in two (or three) axes that is driven by gravity. It involves a transfer of kinetic energy to gravitational potential energy.In conceptual terms: The motion of a simple pendulum is periodic and exhibits properties common to all periodic motion such as a period, the time it takes to complete one cycle. The count of cycles per unit time is known as the frequency. The amount of deflection from the downward rest position is the amplitude. Period is described in units of time. Frequency is described in units of Hertz (Hz), which is defined as one cycle per second.
- In mathematical terms: When characterizing periodic motion, the period or frequency is often directly measured and used to calculate the other term. In the case of pendulums operating at or near the surface of the Earth, gravity is constant throughout the swing and in the case of small amplitudes (θ < 22º results in less than 1% error), a simple pendulum with small-angle approximation equation can be arranged to solve for period (T), length (l) or gravity (g), as shown in Equations 1, 2 and 3, respectively.
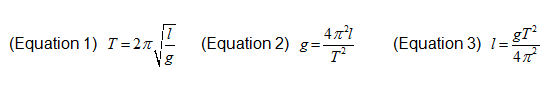
- In process terms: Using Equations 1, 2 and 3, algebraic computations of any term can be found easily given the remaining variables. These equations can be used to find the correct length of a pendulum needed to have a given period, using a given pendulum to calculate the acceleration due to gravity, or calculating the period of a pendulum of particular length. This opens the door for various design questions/problems.
- In applicable terms: Demonstrate simple pendulum motion with a simple pendulum, clock or other examples. Point out the major features of the periodic motion such as the period, frequency and amplitude. By changing the frequency of the motion, it should be apparent that the period is inversely proportional to the frequency. With two demonstrators, you can demonstrate that neither amplitude nor mass have little effect on the period. The effect of pendulum length on period can be investigated with pendulums of varying length. (Note: The units of length and time must be consistent for all variables.)
- In equation terms: The motion of a pendulum is a subset of harmonic motion described by the equation: x(t) = Acos(ωt+φ).
Associated Activities
- Android Pendulums - Students take advantage of the built-in accelerometers in Android devices to set up pendulums and experiment with changes to their properties (amplitude, length, mass). Groups complete formal experiments to alter one variable while keeping all other parameters constant, performing numerous trials, identifying independent/dependent variables, collecting data and using the simple pendulum equation.
Vocabulary/Definitions
amplitude: A periodic variable that is a measure of change over a single period. Typically, it is measured from an object's equilibrium point to its most extreme value.
harmonic motion: A type of periodic motion in which the restoring force is directly proportional to the displacement.
pendulum: A weight suspended from a pivot point such that it can swing freely.
period: The amount time it takes for an object experiencing periodic motion to complete one full cycle and return to the same relative position.
periodic motion: Any motion that repeats over and over again with the same time required for each recurrence.
Assessment
Pre-Lesson Assessment
Questions: Ask students the following questions to assess their base knowledge of the lesson topic:
- When you hear the term periodic motion, what do you think it is?
- Where might you see/experience periodic motion in your daily lives?
- Can you think of examples in which engineers might exploit periodic motion for our benefit?
Post-Introduction Assessment
Observations: As students are engaged in the lesson ask yourself these or similar questions:
- Did students find real-world examples of periodic motion?
- Were students able to relate engineering to periodic motion?
- Are students able to utilize the vocabulary of periodic motion?
Lesson Summary Assessment
Writing Prompts: Assign students to individually write answers to one (or both) of the following prompts:
- Explain where period motion can be found in the world and how it can be beneficial. (Example answer: Periodic motion can be found in the tides, how the stars move, and the natural rhythms of the Earth (the seasons, day and night). It can be found in the mechanical systems that we create to make our lives better. We use it to make predictions about electromagnetic radiation and its effect on life on Earth (the Sun is a complex and somewhat periodic system). Periodic motion is found in all waves that make up light and sound. By manipulating periodic motion we make music. Too many instances exist to even begin to cite them all.)
- Explain how some engineers use the concept of periodic motion in their work. (Example answer: Engineers use periodic motion to design mechanical systems such as motors, generators, clocks and toys. They design instruments to manipulate sound waves to make music of different voices in order to make harmonies. Engineers have used periodic motion to generate energy by using the tides and the Sun, which have periodic aspects.)
Additional Multimedia Support
As part of delivering the Introduction/Motivation content to the class, play a six-minute video, Tacoma Narrows Bridge Collapse "Galloping Gertie," which shows 1940 film footage of a failing suspension bridge, at https://www.youtube.com/watch?v=j-zczJXSxnw.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students explore how pendulums work and why they are useful in everyday applications. In a hands-on activity, they experiment with string length, pendulum weight and angle of release.

Students learn what a pendulum is and how it works in the context of amusement park rides. While exploring the physics of pendulums, they are also introduced to Newton's first law of motion — about continuous motion and inertia.

Students investigate the motion of a simple pendulum through direct observation and data collection using Android® devices. Student groups create pendulums that hang from the classroom ceiling, using Android smartphones or tablets as the bobs, taking advantage of their built-in accelerometers.

Students experientially learn about the characteristics of a simple physics phenomenon — the pendulum — by riding on playground swings. They use pendulum terms and a timer to experiment with swing variables. They extend their knowledge by following the steps of the engineering design process to desi...
Copyright
© 2014 by Regents of the University of Colorado; original © 2013 Board of Regents, University of NebraskaContributors
Doug BertelsenSupporting Program
IMPART RET Program, College of Information Science & Technology, University of Nebraska-OmahaAcknowledgements
The contents of this digital library curriculum were developed as a part of the RET in Engineering and Computer Science Site on Infusing Mobile Platform Applied Research into Teaching (IMPART) Program at the University of Nebraska-Omaha under National Science Foundation RET grant number CNS 1201136. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: June 14, 2019










User Comments & Tips