Quick Look
Grade Level: 10 (9-11)
Time Required: 45 minutes
Lesson Dependency: None
Subject Areas: Chemistry, Life Science, Physical Science
NGSS Performance Expectations:

| MS-PS2-2 |
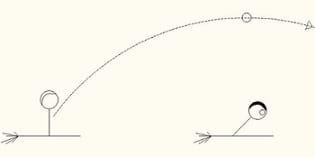
Summary
Students watch video clips from October Sky and Harry Potter and the Sorcerer's Stone to learn about projectile motion. They explore the relationships between displacement, velocity and acceleration and calculate simple projectile motion. The objective of this activity is to articulate concepts related to force and motion through direct immersive interaction based on the theme, The Science Behind Harry Potter. Students' interest is piqued by the use of popular culture in the classroom.Engineering Connection
Engineers from many different disciplines use the concepts of force and motion. Mechanical engineers design all sorts of engines that transport goods and people, machines and tools such as vacuum cleaners and factory assembly equipment that make our ways of life possible, as well as many other types of devices. Structural engineers design houses, bridges and skyscrapers that can withstand everyday forces as well as extraordinary forces, such as earthquakes, monsoons and hurricanes to keep us safe. Aerospace engineers design aircraft, rockets and spacecraft, which includes predicting projectile motion.
Learning Objectives
After this lesson, students should be able to:
- Describe displacement, velocity and acceleration.
- Describe gravity.
- Describe projectile motion and relate it to real-life engineering problems.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS2-2. Plan an investigation to provide evidence that the change in an object's motion depends on the sum of the forces on the object and the mass of the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan an investigation individually and collaboratively, and in the design: identify independent and dependent variables and controls, what tools are needed to do the gathering, how measurements will be recorded, and how many data are needed to support a claim. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | The motion of an object is determined by the sum of the forces acting on it; if the total force on the object is not zero, its motion will change. The greater the mass of the object, the greater the force needed to achieve the same change in motion. For any given object, a larger force causes a larger change in motion. Alignment agreement: All positions of objects and the directions of forces and motions must be described in an arbitrarily chosen reference frame and arbitrarily chosen units of size. In order to share information with other people, these choices must also be shared.Alignment agreement: | Explanations of stability and change in natural or designed systems can be constructed by examining the changes over time and forces at different scales. Alignment agreement: |
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the role of society in the development and use of technology.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Texas - Science
-
compare and contrast potential and kinetic energy;
(Grade
6)
More Details
Do you agree with this alignment?
-
identify and describe the changes in position, direction, and speed of an object when acted upon by unbalanced forces;
(Grade
6)
More Details
Do you agree with this alignment?
-
calculate average speed using distance and time measurements;
(Grade
6)
More Details
Do you agree with this alignment?
-
measure and graph changes in motion; and
(Grade
6)
More Details
Do you agree with this alignment?
-
investigate how inclined planes and pulleys can be used to change the amount of force to move an object.
(Grade
6)
More Details
Do you agree with this alignment?
Pre-Req Knowledge
Some familiarity with displacement, velocity and acceleration.
Introduction/Motivation
(Begin by showing a video clip from October Sky. In the clip, the main character, Homer Hickam, calculates the trajectory of a homemade rocket in front of his science class.)
What happened in that video clip? (Expect students to say that Homer calculated the rocket's trajectory.) How might an engineer's knowledge of how something moves help people? (Expect answers to vary greatly. Possible examples: Engineers use their knowledge of force and motion to make sure that airplanes land in the right places, to design better cars [or other vehicles], to design earthquake-resistant buildings.)
Do you think it is difficult to calculate the projected motion of an object? (Expect students to say yes, because the movie made it look difficult.) It is actually not as difficult as it looks, we are going to do the exact same calculations shown in October Sky today in class. (Proceed to conducting the associated activity Magical Motion.)
Lesson Background and Concepts for Teachers
Classic Equations of Linear Motion
The equations of linear motion describe the behavior of a system as a function of time. The classic equations of linear motion are:
Classic Equations of Linear Motion
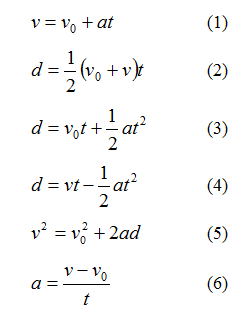
Where:
- t is the amount of time the object was in motion
- d is displacement or the distance between the initial and final positions of the object
- v0 is the initial velocity of the object
- v is the final velocity of the object
- a is the constant acceleration of the object
Using these six equations and given any three of the five parameters, the other two parameters can easily be calculated.
Derivation of Equations
These six equations can be derived from the definitions of acceleration and velocity. Acceleration is the rate of change of velocity over time.
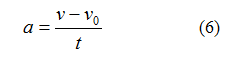
If this equation is rearranged, it becomes Equation 1.
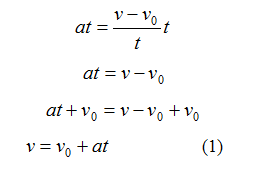
The definition of average velocity is the rate of change of position with respect to time.
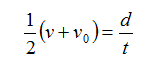
If this equation is rearranged, it becomes Equation 2.
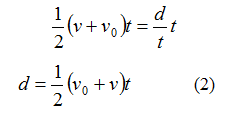
Equation 1 can be substituted into Equation 2 to create Equations 3.
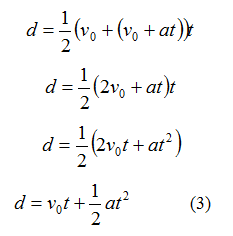
Equation 1 can be rearranged and substitute into Equation 3 to create Equation 4.
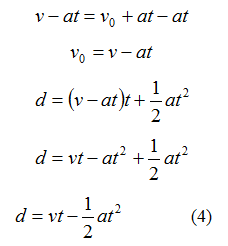
Equation 1 can also be rearranged and substituted into Equation 2 to create Equation 5.
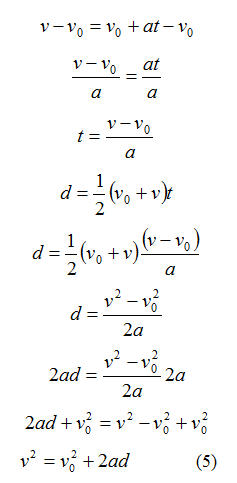
Simple Applications of Equations
These equations can be used to describe the motion of bodies moving in one dimension with constant acceleration. One of the most common applications for these equations is projectile motion, such as a ball being thrown in the air. If one knows either the initial velocity of the ball as it was thrown or the amount of time the ball traveled, one can calculate all five variables. It is also common to calculate the motion of various vehicles and animals using these equations.
Engineering Applications of Equations
Force and motion play a large part in mechanical and structural engineering. Mechanical engineers typically use heat and mechanical power for the design and operation of machines and tools. Mechanical power is directly related to the motion of an object. Mechanical engineers design all sorts of mechanical systems from the vacuum cleaners to cars to machines in factories that mass produce our everyday goods. All of this design is dependent upon being able to calculate motion. Structural engineers design structures that we see all around us including buildings, bridges and dams. While one usually does not consider there structures to be moving (usually they are at equilibrium), they do vibrate due to forces caused by vehicles, wind, earthquakes and severe weather events. This vibration is a motion and must be calculated to ensure that the structures around us are safe.
Associated Activities
- Magical Motion - Students explore the relationships between displacement, velocity and acceleration, and calculate simple projectile motion. They measure the amount of time a thrown remembrall travels in a scene from a Harry Potter movie, make projectile motion calculations and analyze them.
Vocabulary/Definitions
acceleration: The rate of change of velocity with respect to time.
displacement: The difference between the first position of an object and any later position.
velocity: The rate of change of position with respect to time.
Assessment
Written Reflection: At lesson end, assign students to write descriptions of how engineers might use their understanding of force and motion to the application of devices, products, tools and processes for people. Examples: To make sure that airplanes land in the right place, to design a car or any kind of moving vehible, to design earthquake-resistant structures. Review their descriptions to gauge their levels of understanding.
Additional Multimedia Support
Borrow from your school or public library DVDs of the October Sky and Harry Potter and the Sorcerer's Stone movies, so you can show students the invisible ink clips. If not available, describe the scenes, since most students are familiar with the movies and will be able to recall the scenes and describe them more fully to other classmates.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

In this activity, students examine how different balls react when colliding with different surfaces. They learn how to calculate momentum and understand the principle of conservation of momentum.

Students learn the concept of angular momentum and its correlation to mass, velocity and radius. In an associated literacy activity, students use basic methods of comparative mythology to consider why spinning and weaving are common motifs in creation myths and folktales.
References
Dictionary .com. Lexico Publishing Group, LLC. Accessed March 25, 2011. http://www.dictionary.com
Copyright
© 2013 by Regents of the University of Colorado; original © 2011 University of HoustonContributors
Rachel Howser; Christine HawthorneSupporting Program
National Science Foundation GK-12 and Research Experience for Teachers (RET) Programs, University of HoustonAcknowledgements
This digital library content was developed by the University of Houston's College of Engineering under National Science Foundation GK-12 grant number DGE-0840889. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.
Last modified: June 30, 2019






User Comments & Tips