Efficiency of a Water Heating System
What's the efficiency of a water heating system?Copyright NASA http://blogs.nasa.gov/cm/blog/ISS%20Science%20Blog/posts/post_1301433765536.html
Students use a watt meter to measure energy input into a hot plate or hot pot used to heat water. The theoretical amount of energy required to raise the water by the measure temperature change is calculated and compared to the electrical energy input to calculate efficiency.
Engineers strive to improve the energy efficiency of processes, since some energy is lost in each of the conversion processes. They have learned that more complicated processes that have many components are typically less efficient than simple systems. Making systems that include energy conversions more efficient can help to reduce our nation's consumption of fossil fuels and production of greenhouse gas emissions.
After this activity, students should be able to:
- Explain where energy is "lost" in conversions and why based on the second law of thermodynamics.
- Compute the efficiency of an energy conversion given input and output.
- Identify system by-products and explain how they can be used effectively to increase overall system efficiency.
- Use collected data to calculate the efficiency of a system.
CCSS.Math.Content.HSA-SSE.A.1 Interpret expressions that represent a quantity in terms of its context
Grades 9-12
Do you agree with this alignment?CCSS.Math.Content.HSN-Q.A.1 Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
Grades 9-12
Do you agree with this alignment?
Energy can be used to do work, using many processes.
Grades 6-8
Do you agree with this alignment?STEL-8I Use tools, materials, and machines to safely diagnose, adjust, and repair systems.
Grades 6-8
Do you agree with this alignment?
recognize and apply mathematics in contexts outside of mathematics
Grades -1-12
Do you agree with this alignment?select and apply techniques and tools to accurately find length, area, volume, and angle measures to appropriate levels of precision
Grades 6-8
Do you agree with this alignment?use common benchmarks to select appropriate methods for estimating measurements
Grades 6-8
Do you agree with this alignment?relate and compare different forms of representation for a relationship
Grades 6-8
Do you agree with this alignment?model and solve contextual problems using various representations, such as graphs, tables, and equations
Grades 6-8
Do you agree with this alignment?select appropriate methods and tools for computing with fractions and decimals from among mental computation, estimation, calculators, or computers, and paper and pencil, depending on the situation, and apply the selected methods
Grades 6-8
Do you agree with this alignment?work flexibly with fractions, decimals, and percents to solve problems
Grades 6-8
Do you agree with this alignment?solve problems involving scale factors, using ratio and proportion
Grades 6-8
Do you agree with this alignment?solve problems that arise in mathematics and in other contexts
Grades -1-12
Do you agree with this alignment?develop, analyze, and explain methods for solving problems involving proportions, such as scaling and finding equivalent ratios
Grades 6-8
Do you agree with this alignment?understand and use ratios and proportions to represent quantitative relationships
Grades 6-8
Do you agree with this alignment?understand both metric and customary systems of measurement
Grades 6-8
Do you agree with this alignment?
Energy is a property of many substances and is associated with heat, light, electricity, mechanical motion, sound, nuclei, and the nature of a chemical. Energy is transferred in many ways.
Grades 5-8
Do you agree with this alignment?Perfectly designed solutions do not exist. All technological solutions have trade-offs, such as safety, cost, efficiency, and appearance. Engineers often build in back-up systems to provide safety. Risk is part of living in a highly technological world. Reducing risk often results in new technology.
Grades 5-8
Do you agree with this alignment?Develop descriptions, explanations, predictions, and models using evidence. Students should base their explanation on what they observed, and as they develop cognitive skills, they should be able to differentiate explanation from description--providing causes for effects and establishing relationships based on evidence and logical argument. This standard requires a subject matter knowledge base so the students can effectively conduct investigations, because developing explanations establishes connections between the content of science and the contexts within which students develop new knowledge.
Grades 5-8
Do you agree with this alignment?Heat moves in predictable ways, flowing from warmer objects to cooler ones, until both reach the same temperature.
Grades 5-8
Do you agree with this alignment?Mathematics is important in all aspects of scientific inquiry.
Grades 5-8
Do you agree with this alignment?Think critically and logically to make the relationships between evidence and explanations. Thinking critically about evidence includes deciding what evidence should be used and accounting for anomalous data. Specifically, students should be able to review data from a simple experiment, summarize the data, and form a logical argument about the cause-and-effect relationships in the experiment. Students should begin to state some explanations in terms of the relationship between two or more variables.
Grades 5-8
Do you agree with this alignment?Use mathematics in all aspects of scientific inquiry. Mathematics is essential to asking and answering questions about the natural world. Mathematics can be used to ask questions; to gather, organize, and present data; and to structure convincing explanations.
Grades 5-8
Do you agree with this alignment?Technological solutions have intended benefits and unintended consequences. Some consequences can be predicted, others cannot.
Grades 5-8
Do you agree with this alignment?Use appropriate tools and techniques to gather, analyze, and interpret data. The use of tools and techniques, including mathematics, will be guided by the question asked and the investigations students design. The use of computers for the collection, summary, and display of evidence is part of this standard. Students should be able to access, gather, store, retrieve, and organize data, using hardware and software designed for these purposes.
Grades 5-8
Do you agree with this alignment?
A.SSE.1 Interpret expressions that represent a quantity in terms of its context
Grades 9-12
Do you agree with this alignment?N.Q.1 Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
Grades 9-12
Do you agree with this alignment?
MS-PS3-4 Plan and conduct an investigation to determine the relationships among the energy transferred, the type of matter, the mass, and the change in the temperature of the sample of matter.
Grades 6-8
Do you agree with this alignment?
MS-PS3-4 Plan an investigation to determine the relationships among the energy transferred, the type of matter, the mass, and the change in the average kinetic energy of the particles as measured by the temperature of the sample.
Grades 6-8
This resource focuses on the following Three Dimensional Learning aspects of NGSS:
Science & Engineering Practices- Plan an investigation individually and collaboratively, and in the design: identify independent and dependent variables and controls, what tools are needed to do the gathering, how measurements will be recorded, and how many data are needed to support a claim.Do you agree with this alignment?
- Science knowledge is based upon logical and conceptual connections between evidence and explanations.Do you agree with this alignment?
Disciplinary Core Ideas- Temperature is a measure of the average kinetic energy of particles of matter. The relationship between the temperature and the total energy of a system depends on the types, states, and amounts of matter present.Do you agree with this alignment?
- The amount of energy transfer needed to change the temperature of a matter sample by a given amount depends on the nature of the matter, the size of the sample, and the environment.Do you agree with this alignment?
Crosscutting Concepts- Proportional relationships (e.g. speed as the ratio of distance traveled to time taken) among different types of quantities provide information about the magnitude of properties and processes.Do you agree with this alignment?
Do you agree with this alignment?- Plan an investigation individually and collaboratively, and in the design: identify independent and dependent variables and controls, what tools are needed to do the gathering, how measurements will be recorded, and how many data are needed to support a claim.
Each group needs:
- electric water-heating device (such as a hot plate, hot pot, microwave; it is best to have different appliances among the groups)
- thermometer
- graduated cylinder (100 or 500 ml)
- stopwatch
- watt meter (can be shared among groups to some extent)
- insulated pot holder
- Student Worksheet (PDF), one per student
(Start with the combustion activity setup or block diagram on the board as a reference point to what students learned earlier.) Does all of the heat go into heating the water and/or spinning the turbine? Where is energy lost? (Or, at least lost from our ability to do work?) Where does this energy go?
We've already seen the first law of thermodynamics in action – the law of conservation of energy states that energy can neither be created nor destroyed (by ordinary means) - only converted into different forms.
A second law of thermodynamics helps to explain these losses. The heat losses can be called "entropy," which is a measure of how much energy is dispersed to the environment and is no longer usable. The second law of thermodynamics states that the entropy of the universe always increases. That means that things get increasingly disordered and are irreversible (or, there will always be heat losses in any energy conversion process).
Lets look at a simple heating process. (Show an example of a hot pot or other simple water heating device, and draw a process flow diagram.)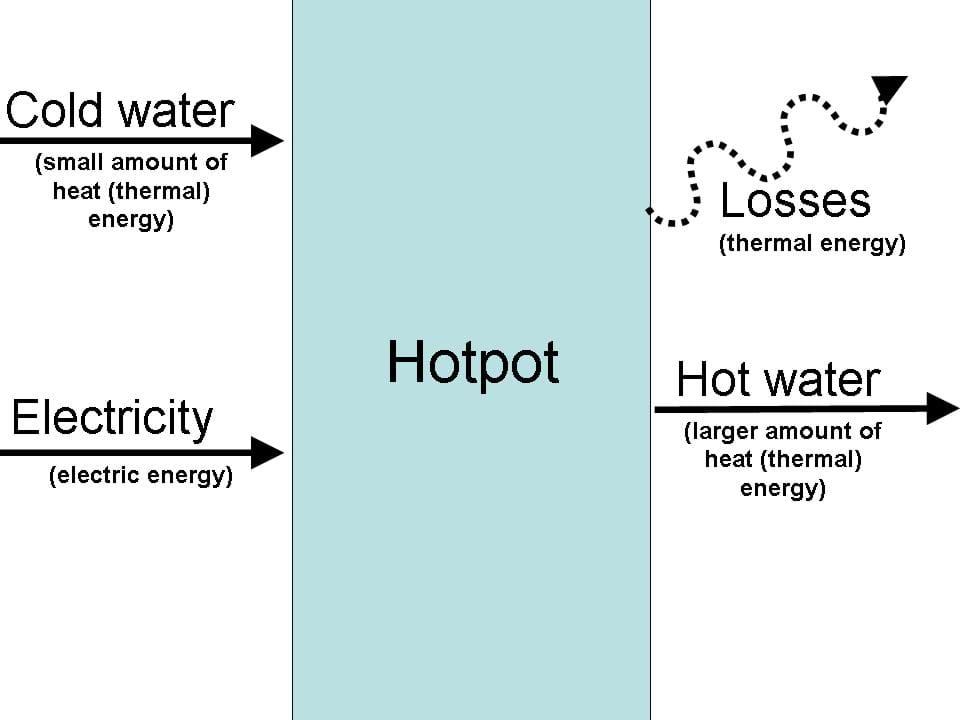
An example block flow diagram for hot pot.Copyright 2008 Clarkson University, Potsdam NY
Explain the system that will be studied in this activity.
- Energy into the system determined by electricity supply.
- Energy = power X time (W s = J)
- We can use a watt meter to measure power and stop watch to measure time.
- The theoretical amount of energy needed to heat a substance such as water can be calculated based on the mass, temperature rise and specific heat of the substance.
Q = m*Cp* ∆T
Where:
- Q is the energy required (joules, J);
- m is the mass of the substance (g) (calculated from volume (V) and density (p) of water, 1 g/ml);
- Cp is the specific heat (J/g/°C)
- ∆T is the change in temperature (°C).
- The specific heat of water is 4.186 J/g/°C. Q = m*Cp*T
- Efficiency is defined as energy in output / energy in input:
- E = (pVCp ∆T)/(Pt)
- If power is used in units of watts and time in seconds, then both the denominator and numerator have units of Joules.
Before the Activity
- Set up stations around the room with all equipment.
- Make copies of the Student Worksheet.
With the Students:
- Show how the watt meter is operated.
- Proceed with the activity.
- Conclude with a class discussion comparing the efficiencies that students found in the various water heating systems. Which system is most efficient? Least? What is it about the design of the system that affects the efficiency?
Worksheets: Collect completed student worksheet to check to make sure calculations are correct and answers to discussion questions show appropriate insight.
Provide potholders or insulated gloves for handling the thermometers and hot water containers.
Contributors
Susan Powers; Jan DeWaters; Clarkson and St. Lawrence University Students (K-12 Project Based Learning Partnership Program)
Supporting Program
Office of Educational Partnerships, Clarkson University, Potsdam, NY
Acknowledgements
This activity was developed under National Science Foundation grant nos. DUE 0428127 and DGE 0338216. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Copyright
2013 by Regents of the University of Colorado; original © 2008 Clarkson University