Quick Look
Grade Level: 5 (4-6)
Time Required: 30 minutes
Expendable Cost/Group: US $1.00
Group Size: 4
Activity Dependency: None
NGSS Performance Expectations:

| 5-ESS2-1 |
Summary
Students develop their understanding of air convection currents and temperature inversions by constructing and observing simple models.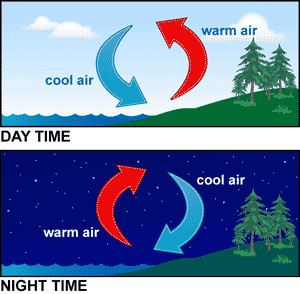
Engineering Connection
Engineers study temperature inversions and convection currents to understand why pollution levels may be higher in some areas than in others. They use this information to reduce pollution levels and determine new pollution prevention programs. They also study convection currents inside buildings to help improve indoor air quality that may be poor due to smoking or fumes from cleaning supplies. Convection currents help to circulate these pollutants, sending them outside of the building.
Learning Objectives
After this activity, students should be able to:
- Understand and explain convection currents.
- Build simple models to investigate convection currents and temperature inversions.
- Understand how engineers study temperature inversions and convection currents to know why pollution levels may be higher in some areas than in others
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
5-ESS2-1. Develop a model using an example to describe ways the geosphere, biosphere, hydrosphere, and/or atmosphere interact. (Grade 5) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop a model using an example to describe a scientific principle. Alignment agreement: | Earth's major systems are the geosphere (solid and molten rock, soil, and sediments), the hydrosphere (water and ice), the atmosphere (air), and the biosphere (living things, including humans). These systems interact in multiple ways to affect Earth's surface materials and processes. The ocean supports a variety of ecosystems and organisms, shapes landforms, and influences climate. Winds and clouds in the atmosphere interact with the landforms to determine patterns of weather. Alignment agreement: | A system can be described in terms of its components and their interactions. Alignment agreement: |
International Technology and Engineering Educators Association - Technology
-
The use of technology affects the environment in good and bad ways.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
State Standards
Colorado - Science
-
Develop and communicate an evidence-based scientific explanation for changes in weather conditions
(Grade
5)
More Details
Do you agree with this alignment?
-
Use data collection tools and measuring devices to gather, organize, and analyze data such as temperature, air pressure, wind, and humidity in relation to daily weather conditions
(Grade
5)
More Details
Do you agree with this alignment?
Materials List
Demo 1: Warm Air is Less Dense than Cool Air
- 1 empty, two-liter plastic bottle
- 1 balloon
- 1 large bowl
- Hot water
- Ice
Student Activity: Spinning Snakes
- Spinning Snake Worksheet, 1 per student
- Scissors, 1 per student
- Thread
- Colored pencils, crayons, markers, etc.
Demo 2: Convection Current Model
- 2 aquariums (or very large glass jars/beakers)
- 2 small plastic bags with strong seals
- Dark-colored food coloring
- Bowl (to mix water, ice and food coloring)
- 1 long straight pin
- 1 long-handled spoon or ladle
- Water
- Ice cubes
- Hot plate/microwave/stove (optional; required only if tap water is not hot enough)
- Pan or cooking container (optional; to heat water on hot plate/microwave/stove)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_air_lesson04_activity4] to print or download.Introduction/Motivation
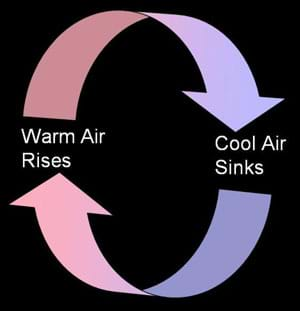
As air warms, it rises and cold air moves in to take its place. Also, warm air cools as it rises and then starts to sink again. This happens because warm air is less dense than cold air. This process causes currents of air to move around inside buildings and outdoors. Birds and gliders rise on warm air currents called thermals. This movement of air is called a convection current.
Typically, air temperature is warmer near the ground than it is at high altitudes. Sometimes a blanket of cold air is trapped beneath a thick layer of warm air and so the temperature actually increases with height. This reversed layering is called a temperature inversion. The air near the ground does not circulate, so pollutants build up in the cold air near the surface (see Figure 2). Air quality becomes unhealthy, and it may last for weeks.

How can a temperature inversion affect air pollution and you? In October 1948, the people in the industrial city of Donora, PA, experienced a temperature inversion. Donora was an extremely polluted city and people thought that pollution was the price they had to pay for "progress." This particular temperature inversion lasted four days! During this time, people could barely see, they had severe eye irritations and chest pains, animals became sick, 20 people died and thousands were hospitalized. Today, temperature inversions are common in Los Angeles, CA, resulting in more than 200 unhealthy air days per year in that city! Temperature inversions also happen occasionally in other locations, too.
This layer of warm air aloft is also the reason freezing rain occurs. Additionally, it can be difficult to forecast accurate temperatures during times of strong temperature inversions.
Why do Engineers Care?
Engineers study temperature inversions and convection currents to understand why pollution levels may be higher in some areas than in others. They use this information to reduce pollution levels and determine new pollution prevention programs. They also study convection currents inside buildings to help improve indoor air quality that may be poor due to smoking or fumes from cleaning supplies. Convection currents help to circulate these pollutants, sending them outside of the building.
To create good indoor air circulation, engineers design heating and air conditioning systems in ways that establish convection currents. Have you ever noticed that heat-producing baseboards, radiators and vents are located near the floor instead of near the ceiling? A well-designed system can save energy because convection currents move the air instead of fans.
Procedure
Before the Activity
- Gather materials and make copies of the Spinning Snake Worksheet.
With the Students
Lead a brainstorming session with the question: What is a temperature inversion? Encourage wild ideas and write them on the board. Do not evaluate ideas or give the answer, but tell students they will learn more about this topic during the activity.
Demo 1: Warm Air is Less Dense than Cool Air
- Fit the mouth of the balloon over the mouth of the empty, two-liter bottle (see Figure 3).
- Stand the bottle in the center of the bowl. Fill the bowl with hot water, around the outside of the two-liter bottle (see Figure 3).
- After a few minutes, notice the balloon start to inflate.
- Carefully pour the water out of the bowl and fill the bowl with ice (see Figure 3). What happens?

- Ask students why the balloon inflated and deflated in response to the hot and cold water. Explanation: When air is warmed, it expands and needs more space, so it stretches out the balloon. When air is cooled, it contracts and needs less space, so the balloon deflates. In this closed system, the mass of air in the bottle remains constant, so this shows that the warm air requires more space (and thus is less dense, based on the fact that density = mass/volume) than the cool air. Warm air rises because it is less dense than cold air.
Student Activity: Spinning Snakes
- Distribute a Spinning Snake Worksheet to each student.
- Have the students color their snakes.
- Ask the students to cut the snake along the spiral lines.
- Attach a thread to the head of the snake.
- Hang the snake near the radiator or other heat source (or, at different places around the room, for comparison purposes).
- Observe the snakes carefully.
- Which direction does it turn? Can you explain why it turns different directions in different places?
Demo 2: Convection Current Model
- To create a model of typical atmospheric conditions (normal convection currents), heat a pan of water on a hot plate and add a few drops of food coloring to the water. Fill one of the aquariums about 3/4 full of cold water and add several ice cubes to it.
- Fill one of the plastic bags half full with warm water heated on the hot plate. Seal the plastic bag so there is no air in the bag.
- Remove the ice cubes from the aquarium. Lower the bag with the warm, colored water (representing air pollution) into the cold, colorless water of the aquarium.
- Without disturbing the water in the aquarium, poke a hole in the bag with the pin and observe the interaction of the warm water with the cold water. What happens when the warm water enters the cold water?
- To simulate a temperature inversion, add several ice cubes and several drops of food coloring to a bowl of water.
- In another container, heat several quarts of water with which to fill the second aquarium about 3/4 full.
- Fill the second plastic bag about half full with the cold, colored water, and seal it so there is no air in the bag.
- Lower the bag with the cold, colored water (representing air pollution) into the warm, colorless water of the aquarium.
- Without disturbing the water in the aquarium, poke a hole in the bag with the pin and observe the interaction of the cold water with the warm water. What happens when the cold water enters the warm water?
Vocabulary/Definitions
Convection current: The movement of air due to temperature differences.
Temperature inversion: When an upper thick layer of warm air traps a lower layer of cold air close to the Earth, causing the temperature to be warmer at higher elevations.
Assessment
Pre-Activity Assessment
Brainstorming: As a class, have the students engage in open discussion. Encourage wild ideas and discourage criticism of ideas. Do not evaluate ideas or give the answer, but tell students they will learn more about the topic during the activity. Have them raise their hands to respond. Write ideas on the board. Ask the students:
- What is a temperature inversion?
Activity Embedded Assessment
Question/Answer: Ask the students the questions at the end of each demo and activity in the Procedure section, and discuss as a class.
Post-Activity Assessment
Define it! Drawing: Have students draw pictures of a temperature inversion and write a descriptive explanation of a temperature inversion, how it occurs and its effects.
Safety Issues
- Students should be mindful when handling scissors and glass containers.
- Students should be careful not to slip on wet floors and make sure to clean up any spills as soon as they happen.
Troubleshooting Tips
Use a dark color of food coloring.
Use a lot of food coloring so as to create more "visible pollution" in the aquariums.
It might be necessary to poke several holes in the bags to speed up the activity.
The plastic bag tends float to the top, so use the long-handled spoon to hold down the bag, or hold it there with your hand.
Alternate materials: Use a mason jar instead of an aquarium, and a baby food jar with holes poked in the lid instead of a plastic bag.
It is easy to think that the warm air in the two-liter bottle just rises, but this is incorrect. If it were rising, something else would have to take its place at the bottom of the bottle and since this is a closed system this is impossible. Be sure students understand that the air is expanding (taking up more space), not simply rising.
Activity Extensions
Make connections to other types of convection currents, such as those inside the Earth that cause continental drift.
Look at patterns of convection currents around the globe. Do the large air masses move in the same ways?
Activity Scaling
- These demos and student activity are also appropriate for lower grades.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to the concepts of air pollution and technologies that engineers have developed to reduce air pollution. They develop an understanding of visible air pollutants with an incomplete combustion demonstration, a "smog in a jar" demonstration, construction of simple particulate ma...

Students are introduced to the concepts of air pollution, air quality, and climate change. The three lesson parts (including the associated activities) focus on the prerequisites for understanding air pollution. First, students use M&M® candies to create pie graphs that express their understanding o...
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Amy Kolenbrander; Daria Kotys-Schwartz; Janet Yowell; Natalie Mach; Malinda Schaefer Zarske; Denise CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: August 7, 2020




User Comments & Tips