Quick Look
Grade Level: 6 (5-7)
Time Required: 30 minutes
Expendable Cost/Group: US $0.20
Group Size: 2
Activity Dependency: None
Subject Areas: Earth and Space, Measurement, Number and Operations, Physical Science, Problem Solving, Science and Technology
Summary
Students learn about Pascal's law, an important concept behind the engineering of dam and lock systems, such as the one that Thirsty County wants Splash Engineering to design for the Birdseye River (an ongoing hypothetical engineering scenario). Students observe the behavior of water in plastic water bottles spilling through holes punctured at different heights, seeing the distance water spurts from the holes, learning how water at a given depth exerts equal pressure in all directions, and how water at increasing depths is under increasing pressure.
Engineering Connection
An understanding of Pascal's law and hydrostatic pressure applies in many engineering and scientific fields. Engineers who design locks and dams use the known relationships between water depth and water pressure, as described in pressure laws, to estimate the amount of force expected to be exerted. They use these calculations to design functional structures that adequately meet community performance and safety objectives.
Learning Objectives
After this activity, students should be able to:
- Explain Pascal's law.
- Know that water pressure increases with depth.
- Calculate volume.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
SEP.1.6-8.3.
Analyze and interpret data to provide evidence for phenomena.
(Grades 6 - 8)
More Details
Do you agree with this alignment?
-
SEP.12.6-8.1.
Use mathematical representations to describe and/or support scientific conclusions and design solutions.
(Grades 6 - 8)
More Details
Do you agree with this alignment?
-
SEP.7.3-5.6.
Make observations and measurements to produce data to serve as the basis for evidence for an explanation of a phenomenon.
(Grade 5)
More Details
Do you agree with this alignment?
Common Core State Standards - Math
-
Represent real world and mathematical problems by graphing points in the first quadrant of the coordinate plane, and interpret coordinate values of points in the context of the situation.
(Grade
5)
More Details
Do you agree with this alignment?
-
Apply the formulas V = l × w × h and V = b × h for rectangular prisms to find volumes of right rectangular prisms with whole-number edge lengths in the context of solving real world and mathematical problems.
(Grade
5)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Engage in a research and development process to simulate how inventions and innovations have evolved through systematic tests and refinements.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Represent real world and mathematical problems by graphing points in the first quadrant of the coordinate plane, and interpret coordinate values of points in the context of the situation.
(Grade
5)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multidigit decimals using standard algorithms for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Apply the formulas V = l w h and V = b h to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.
(Grade
6)
More Details
Do you agree with this alignment?
Colorado - Science
-
Use tools to gather, view, analyze, and report results for scientific investigations about the relationships among mass, weight, volume, and density
(Grade
6)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 2-liter plastic soda bottle (ask students to bring from home)
- (optional) Bottle Template and Rulers; prepare bottle by printing and cutting out this template for drilling bottle holes
- ruler or tape measure (or make rulers by printing Bottle Template and Rulers on paper or overhead transparency sheets and cutting into strips)
- 2 strips of duct tape for covering holes
- drill with ~1/8-in bit (have students mark hole and teacher drill, or drill bottle holes before activity), or a sharp-pointed object to punch 1/8-in holes
- water from a faucet or large container
- sink or basin to catch water (unnecessary if working outside)
- stopwatch (or wall clock with second hand)
- Pascal's Law Worksheet
- calculator
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_dams_lesson03_activity1] to print or download.Pre-Req Knowledge
Multiplication using a calculator.
Introduction/Motivation
Water creates large forces on dams, and engineers calculate the amount of those forces to figure out how big and sturdy dams and locks must be. How do you think engineers actually figure out the amount of force? They must figure out the amount of pressure that the water will apply to the structure. To do this, engineers use a special "law" that has to do with water pressure, called Pascal's law. Today we will learn about this water pressure law.
Pascal's law describes the characteristics of water pressure; it says that water at a certain depth has a certain pressure. If you are comparing very deep water to shallow water, do you think they have the same pressure? The deep water has a higher pressure. Why? (Take suggestions from the students.)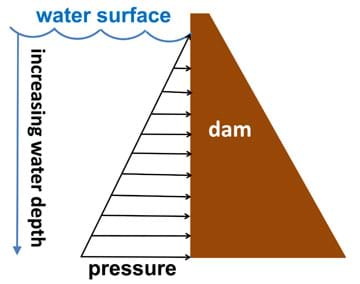
Water is heavy!! One gallon of water weighs 8.3 lbs (or 3.8 kg)!! Since there is no water above the surface (by definition), the water pressure at the water surface is zero. As you move further down, more water is pushing down from above, and the pressure goes up. This means that pressure changes with depth. Pascal's law tells us that if we know the height of water above a location, we can calculate the pressure at that location. In a reservoir behind a dam, where do you expect to find the highest pressures? At what spot on the dam do you find the most water above it? (Draw a picture on the board or overhead projector so students can see why the pressure is highest at the bottom of the dam!)
How do engineers use this information when designing a dam or a lock? Imagine a dam that is built into a deep, steep gorge in a river canyon. In this case, the water level against the dam is high, so you can bet that the pressure exerted by the water near the bottom of the dam is very high. Since engineers know this, they design dams to be able to handle more pressure at the bottom than at the top. That is why many dams are thicker at the bottom than they are at the top!
(In our ongoing, hypothetical, project...) The residents of Thirsty County have complained to Splash Engineering, which is the company you work for, that the Birdseye River is sometimes too shallow in the summer. This means that certain bigger boats cannot pass through, and everyone loses money and access. In addition to having a dam to provide a water supply and hydropower, Thirsty County would also like a dam and lock system at the major Birdseye River crossing to make sure that boats can get through at all times of the year, even during a drought, when the water level is low. Let's learn how to use Pascal's law so you can design a dam and lock system.
You, as the engineers at Splash Engineering, must remember that the dam and lock system you design for Thirsty County must withstand high pressures, especially at the bottom. Let's do an activity so we better understand Pascal's law and water pressure.
Procedure
This activity can be conducted three different ways:
- As one large group led by the teacher
- In two large groups either led by the teacher or student-led (this option results in two sets of the same graphs to compare)
- With students working in pairs using bottles brought from home; they make bottle set-ups and then experiment
Before the Activity
- Gather materials and make copies of the Pascal's Law Worksheet.
- If teaching as a class activity, prepare a 2-liter bottle with holes and measurement scales above the holes using the attached Bottle Template and Rulers.
- If students will be conducting the activity, print the Bottle Template and Rulers attachment on paper — or even better — on overhead transparency sheets.
With the Students
- Divide the class into groups, depending on how you plan to conduct the activity (two groups or student pairs) and pass out the materials and worksheets to each group.

Use the template to determine where to drill holes in the plastic bottle. - As a class, go over the pre-activity assessment and prediction questions. Describe Pascal's law (water pressure increases with water depth!) and have students fill out the Definition section of their worksheets.
- Cut out the Bottle Templates and Rulers template where marked on the template; tape the strips to the bottle. Using a 1/8-in drill bit (or a sharp-pointed object), make holes where the template denotes.
- Make sure that all holes are the same size, and nothing is blocking the holes.
- Place strips of duct tape (with a corner folded back to make removal easier) over the holes.
- Pause and ask students to fill out the Hypothesis section of the worksheet.
- Place the bottle(s) in a sink or basin to catch the leaking water.
- Fill the bottle(s) with water.
- Get ready to observe and compare the streams that come out of each hole when the tape is removed.
- Each bottle experiment has six jobs: 1) timekeeper, 2) tape puller, 3) height measurer, 4) height recorder, 5) distance measurer, 6) distance recorder. Assign a timekeeper in each group who will either use the stopwatch, or watch the wall clock and announce to the group when 30 seconds and 60 seconds have passed.
- When you are ready to start, have the "tape puller" remove the tape from Hole A and the "timekeeper" make note of the starting time (or press Start on the stopwatch). Have the timekeeper update the group members every 5 seconds. At 30 seconds, the "height measurer" looks at the ruler above the hole and tells the "height recorder" the height of the water above the hole. At the same time, the "distance measurer" measures how far the water is shooting from the side of the bottle (5 cm below hole) and reports this to the "distance recorder" to write on the worksheet.

One measurement is the distance the water shoots from the hole. - Refill the bottle, and repeat Step 11 using Hole B (13 cm from bottom), instead of Hole A.
- Have each group share their data with other teams so that each member has the table filled in on the worksheet.
- Working as a group, have each student graph the data for Hole A and Hole B on the blank graphs provided.
- Complete the Conclusions section of the worksheet. Then use calculators to answer the questions on page 2 of the worksheet.
- As a class, revisit the predictions made before the activity, as described in the Assessment section.
- End the lesson with a class discussion comparing results and conclusions. Water in a bottle spills through two holes at the same height with equal pressure in all directions. Water at increasing depth is under increasing pressure.
Vocabulary/Definitions
dam: A barrier to obstruct the flow of water, especially one made of earth, rock, masonry and/or concrete, built across a stream or river.
engineer: A person who applies her/his understanding of science and math to creating things for the benefit of humanity and our world.
lock: An enclosed chamber in a waterway with watertight gates at each end, for raising or lowering vessels from one water level to another by admitting or releasing water.
Pascal's law: A hydrostatics principle that says that for all points at the same absolute height in a body of fluid, the pressure is the same, even if additional pressure is applied on the fluid at some place.
pressure: The exertion of force upon a surface by an object, fluid, etc., in contact with it. Expressed as force per unit area.
Assessment
Pre-Activity Assessment
Discussion Questions: Solicit, integrate and summarize student responses to the following statement and questions. Say you have a plastic soda bottle with a hole punched in it, like we will have in this activity. After filling the bottle with water, the water will stream through the hole.
- What does it mean if the water streams fast vs. slow? (Answer: The speed of the water stream is related to the pressure of the water.)
- Does a fast stream mean that the water has relatively high pressure or relatively low pressure? (Answer: Relatively high pressure.)
Prediction: Have students make predictions by voting with raised hands to each possible answer:
- Will water from a hole near the bottom of the bottle have more or less pressure than that from a hole near the top of the bottle? (Tally the votes and write the numbers on the board. Answer: Tell students that this is exactly what they will discover in the activity. Do not reveal the answer [higher pressure] until after the activity.)
Activity Embedded Assessment
Worksheet: Have students complete the Pascal's Law Worksheet. Make sure they write a hypothesis before starting the activity. Review their answers to gauge their mastery of the subject.
Post-Activity Assessment
Prediction Analysis: Have students compare their initial predictions with their test results, as recorded on their worksheets.
Engineering Drawings: Ask students to create preliminary drawings as if they were engineers from Splash Engineering designing a dam and lock system for Thirsty County. Require that the drawings illustrate where on Birdseye River the dam and lock structure will be built, the dimensions of the structure (how long, wide and deep), and the number of locks in the structure. For an added challenge of constraining the students' designs, tell them that the river is 50m wide and 8m deep, and the largest vessel allowed to pass through is 10m long.
Investigating Questions
- What is volume? (Answer: Volume is the amount of three-dimensional space an object occupies. Engineers usually describe the amount of water in a reservoir using "cubic feet" or "cubic meters," which are liquid measurements of volume. Another unit of liquid volume is a "gallon.")
- Why must an engineer know the volume of the water in a reservoir? (Answer: Water creates large forces on dams and locks. The greater the volume of water held back by a structure, the greater the pressure exerted on the walls of the structure. Engineers must be able to calculate volume to know how big and sturdy dams and locks must be to withstand the forces.)
Safety Issues
- Remind students to be careful when drilling holes.
- Make sure students wipe up any spilled water on the floor to prevent slipping.
Troubleshooting Tips
It is important to drill the holes since the holes MUST be the same size for the activity to work well.
Activity Extensions
Mystery Hole: Add another hole to the bottles and have each group collect the data for their hole. Have teams exchange data with another group and determine the height of the hole for that data. See who can get the closest.
Activity Scaling
For lower grades, drill the holes in the cups in advance to assure proper flow through the holes. Also, have students work in teams of three or four students each.
For upper grades, have students work individually. Ask them to come up with other applications of Pascal's law (such as hydraulic machines, braking systems, wells, elevated water towers, scuba diving safety, etc.).
Additional Multimedia Support
See the US Army Corps of Engineers' animation of a barge going through a dam and lock at: http://www.mvp.usace.army.mil/navigation/default.asp?pageid=166
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to the structure, function and purpose of locks and dams, which involves an introduction to Pascal's law, water pressure and gravity.

Students are introduced to the basic biology behind Pacific salmon migration and the many engineered Columbia River dam structures that aid in their passage through the river's hydroelectric dams. Students apply what they learn about the salmon life cycle as they think of devices and modifications t...

Students learn about the importance of dams by watching a video that presents historical and current information on dams, as well as descriptions of global water resources and the hydrologic cycle. Students also learn about different types of dams, all designed to resist the forces on dams.

Through eight lessons, students are introduced to many facets of dams, including their basic components, the common types (all designed to resist strong forces), their primary benefits (electricity generation, water supply, flood control, irrigation, recreation), and their importance (historically, ...
References
Dictionary.com. Lexico Publishing Group, LLC. Accessed July 17, 2009. (Source of some vocabulary definitions, with some adaptation) http://www.dictionary.com
Locks and Dams. 2006. Newton's Apple Teaching Guides. Twin Cities Public Television. Accessed July 14, 2009. http://www.newtonsapple.tv/TeacherGuide.php?id=1041
Copyright
© 2008 by Regents of the University of Colorado.Contributors
Megan Podlogar; Jeff Lyng; Kristin Field; Denali Lander; Lauren Cooper; Timothy M. Dittrich; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: April 8, 2024









User Comments & Tips