Quick Look
Grade Level: 9 (8-10)
Time Required: 1 hours 30 minutes
(can be split into two 45-minute sessions)
Expendable Cost/Group: US $0.00
Group Size: 4
Activity Dependency:
Subject Areas: Geometry
Summary
Students learn about regular polygons and the common characteristics of regular polygons. They relate their mathematical knowledge of these shapes to the presence of these shapes in the human-made structures around us, especially trusses. Through a guided worksheet and teamwork, students explore the idea of dividing regular polygons into triangles, calculating the sums of angles in polygons using triangles, and identifying angles in shapes using protractors. They derive equations 1) for the sum of interior angles in a regular polygon, and 2) to find the measure of each angle in a regular n-gon. This activity extends students’ knowledge to engineering design and truss construction. This activity is the middle step in a series on polygons and trusses, and prepares students for the Polygon and Popsicle Trusses associated activity.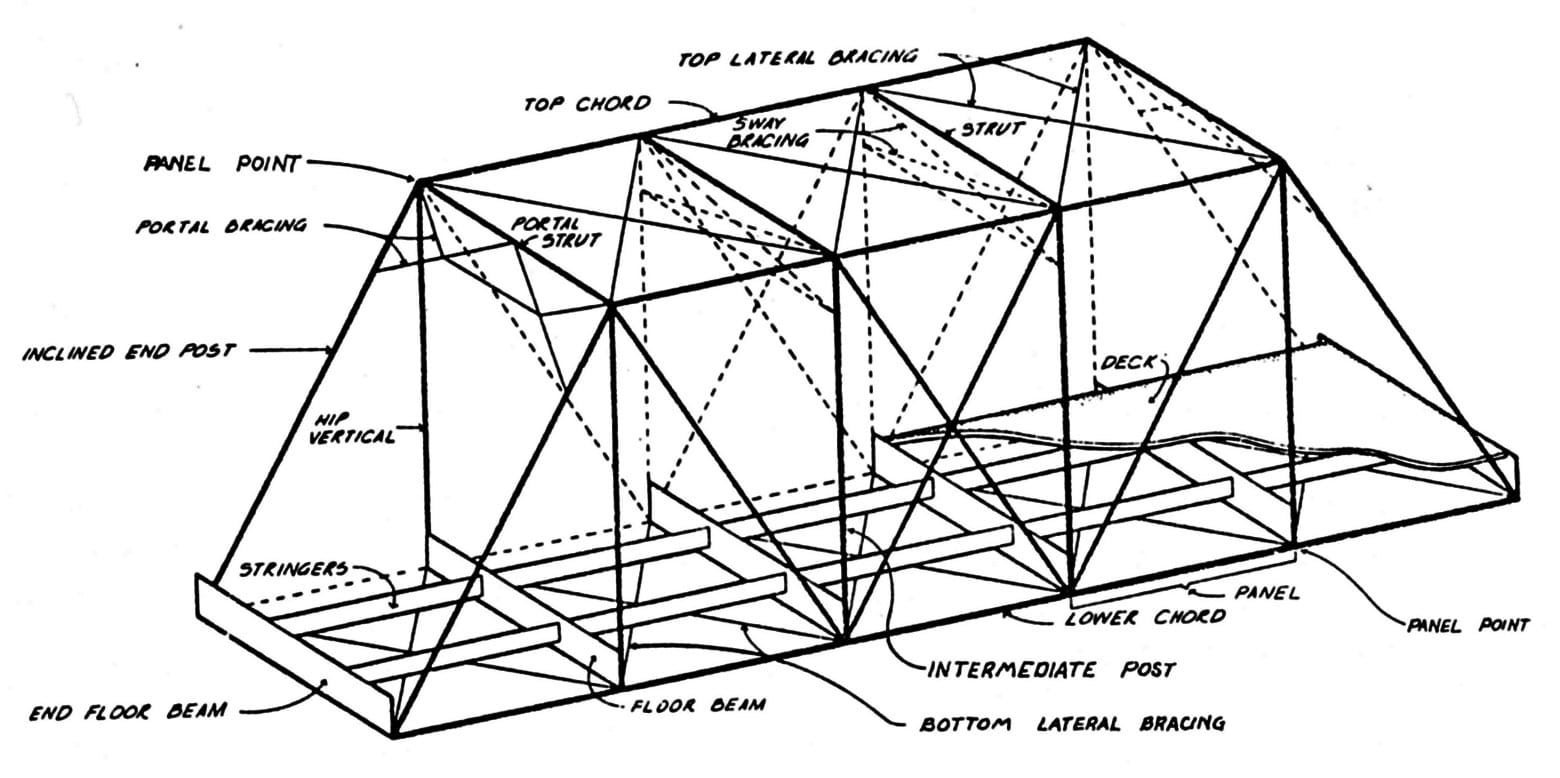
Engineering Connection
Civil engineers design buildings, bridges and towers using basic shapes such as triangles and squares. To make sure the structures are stable and safe, they design them to be able to withstand the anticipated loads without any deformation or bending. They make precise and accurate specifications and measurements, and then double-check their plans by making estimates to verify that the calculations are reasonable. Through this activity, students come to see trusses from an engineering point of view—as unique compositions of polygon shapes that are further broken down into triangle shapes, which serve as the strongest and least deformable shapes.
Learning Objectives
After this activity, students should be able to:
- Explain the components and common characteristics of regular polygons.
- Explain how to find the sum of the interior angles in a polygon of n sides.
- Develop an equation that shows the relationship between the number of sides of a polygon and the sum of its interior angles.
- Explain how the geometry of shapes impacts engineering bridge and truss design and stability.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Infrastructure is the underlying base or basic framework of a system.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Use geometric shapes, their measures, and their properties to describe objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- pencils and blank paper
- ruler or straightedge
- protractors
- KWL Chart, one per student
- Sum of Angles in Polygons Worksheet, one per student
To share with the entire class:
- some example photographs and diagrams of truss designs, bridges and other truss structures to show the class (digital or hardcopy); search online for “truss bridge” images; look at NCDOT’s images of truss bridge designs at https://www.ncdot.gov/initiatives-policies/Transportation/bridges/historic-bridges/bridge-types/Pages/truss.aspx
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_polygons_angles_trusses_lesson01_activity1] to print or download.Pre-Req Knowledge
Ability to use a protractor to measure angles.
Introduction/Motivation
When you look at buildings and structures, what geometric shapes do you notice? What shapes do you see in bridges? What shapes make up a truss? (After each of these questions, listen to student answers. Expect them to suggest shapes such as triangles, squares, pentagons, semicircles, arches, etc.) As evidenced by all your answers, it is clear that the human-made structures around us are composed of many different shapes.
Today we are going to specifically talk about triangles and trusses. First, what is a truss? (Listen to student definitions.) That’s right, a truss is a structural form in which individual structural members are joined to provide increased strength—more strength than would be provided by using a single member. Where have you seen examples of trusses? (Listen to student answers. Expect them to describe bridges that cross rivers, bridges over the highway, buildings, the Eiffel tower, railings and gates, log cabins, interior design, highway ramps, radio towers, electrical towers, cranes, etc.).
(Engage students in a brief discussion. Begin by showing the class some photographs and diagrams of bridges, trusses and other 3D structures.) Why is it important that engineers carefully consider the structure and design of the trusses that they create? (Listen to students’ comments and answers and record them on the classroom board. Possible answers include: For safety purposes, stability, reliability, dependability, serviceability, to avoid structural failure, to protect lives and property, etc.)
(Hand out the KWL Charts.) Now that we know a little bit more about trusses and the shapes used to construct them, let’s review what you already know about certain shapes. Take four minutes and think to yourselves about what you already know about shapes and polygons, filling in the K and W parts of your chart.
Now, brainstorm with the people sitting near you and discuss what you all know and want to know about polygons. You have another four minutes. If you find yourself unsure about a certain concept about or aspect of polygons, make sure to record that in the W section of the chart. Add facts about polygons to your charts and be prepared to share your ideas with the class. (Give students time to talk with partners.)
(Lead a short class discussion about polygons, since they are featured in truss design. Guide the discussion into talking about the angles inside of triangles and how we can calculate them, including calculating the sum of all interior angles in any polygon.) To find the measure of an angle inside a regular polygon, we must divide the polygon into triangles. How do we calculate the sum of all interior angles in any polygon? Since we know the sum of the angles in a triangle is always 180°, we can use the number of triangles we found and the number of degrees in a triangle to calculate the sum of all of the interior angles in any polygon. What are important things to consider when thinking about shapes in construction, especially with respect to how shapes behave under a load, such as in a truss bridge? (Expect students to know that triangles serve as the strongest basic shape.)
What is a regular polygon? (Listen to student definitions.) A regular polygon is a shape that has equal angles and equal sides. Regular polygons are also called convex polygons. Now that we know what a polygon is, we need to be able to calculate the angles inside polygons. Engineers need to know about the angles in their bridge designs to determine the likelihood of deformation under loads, which helps them determine the structural stability of bridges.

Next, let’s derive (come up with) an equation to calculate the total sum of the angles in any polygon using what we already know about the sum of angles in a triangle. To do that, let’s break down the polygon shapes into triangles by drawing lines from a single vertex—which is a point where two lines meet (see Figure 1). This gives us practice in preparation for the next activity, where we will act as engineers and design and build our own bridge truss designs composed of different polygons. We’ll be able to quickly calculate the sum of interior angles before adding weight to our bridges, and then compare that to the angles after the compression loading, in order to see the deformation of our trusses.
Procedure
Before the Activity
- Gather materials.
- Make copies of the KWL Chart and Sum of Angles in Polygons Worksheet.
- Find some example photographs and diagrams to show the class a variety of truss designs, bridges, towers and other truss structures. Be ready to show students these images (digital or hardcopy) during the presentation of the Introduction/Motivation content.
- Review the procedure in full, including the test process.
With the Students
- Start the activity with a discussion of shapes. Use the concept review questions provided in the Assessment section.
- Present the Introduction/Motivation section. (15 minutes) During this time, students share examples of geometric shapes they see in buildings and structures, and their own examples of trusses they have seen; the teacher writes them on the board. The teacher shows photo and diagram examples of trusses. They discuss the value of trusses to engineering designs (strength under loads). Students fill in the K (know) and W (want to know) portions of their KWL Charts, and then pair-share with partners. They discuss polygons and angles, which are part of truss designs, including breaking down polygons into triangles. The teacher makes a connection between these concepts and the next associated activity in which students design and build model truss bridges.
- Divide the class into groups of three or four students each.
- Hand out the worksheet. Give teams ~15 minutes to complete question #1, drawing polygon shapes on blank paper using rulers and/or straightedges, two per person, from the list of eight regular polygons listed on the worksheet.
- Demonstrate and work through worksheet question #2 with students. (10 minutes)
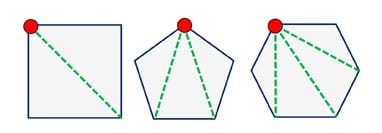
- Have students move on to completing worksheet Part 2 with their groups, during which they fill in a table with data about the polygons: number of sides, number of triangles formed, sum of all angles (in degrees) and how many degrees for each polygon’s angles. (~15 minutes)
- Class discussion: As a class, follow up with students and their progress on the data table. Ask them to tell you what they determined for the equation to find the sum of degrees in a polygon with n sides. Write the equation on the classroom board and ask students to explain what is going on with each part of the equation. (5 minutes)
- Direct students to start worksheet Part 3, during which they try out their equations. (10 minutes; if not completed, assign the rest of the worksheet for homework)
- Direct the groups to check their answers with someone from another group (pair-share) and then hand in completed worksheets (one per group). (5 minutes)
- Direct students to discuss in their groups what they learned about polygons and their interior angles, filling out the L sections of their KWL Charts. This is a time for students to reflect, recap and make connections. (10 minutes)
- As time permits, conclude with the post-activity assessment discussion to make the connection from polygons to bridge and truss design and stability and make a point about the importance of learning from failure, as described in the Assessment section, which leads into the associated activity, Polygon and Popsicle Trusses. (5 minutes)
Vocabulary/Definitions
interior angle: An angle on the interior of a polygon. Formed by two sides of the polygon that share an endpoint.
regular polygon: A polygon that has all equal sides and all equal angles. Also called a convex polygon.
structural load: Forces that apply to a structure, such as the weight of something applied to the top, sides and/or floors of a structure.
truss: A structural form made from the joining of individual structural members that form triangles or other stable, rigid shapes. Due to its geometric rigidity, a truss distributes weight from a single point over a wider area.
vertex (geometry): The point in geometric shapes where two lines meet. Plural is vertices.
weight : The force exerted on a body by gravity.
Assessment
Pre-Activity Assessment
Concept Review: As a class, ask students: Describe the differences between different regular polygons. What are the components that make up polygons? (Answer: Sides and angles.) What other characteristics are common to all regular polygons? (Answer: In each regular polygon, its sides are all equal in length and its angles are all the same. Also, the number of sides equals the number of angles.) Must the number of sides equal the number of angles? (Answer: Yes) Knowing these facts about polygons is important for completing the activity.
Activity Embedded Assessment
Deriving Equations: As student teams work on the Sum of Angles in Polygons Worksheet, they are guided to derive the equation for the sum of interior angles in a regular polygon, and the equation to find the measure of each angle in a regular n-gon. Refer to the answers in the Sum of Angles in Polygons Worksheet Answer Key. Review their answers and work to gauge their depth of understanding.
Post-Activity Assessment
Learning from Structural Failure: Tell students: The reason someone might want to know the angles inside of various shapes is to determine how much a shape’s angle changes when subjected to a load. Think about engineers who are designing bridges. They want their bridges to support large amounts of weight. They do not want any deformation or bending in their bridges. Sometimes bridges collapse and those failures are important opportunities for engineers to analyze at what angles and loads the bridges failed. Then, they can use what they learn to improve on the original designs and create better bridges.
Activity Extensions
Have students cut out their polygon shapes and then cut them into triangles. Doing this provides a tangible and visual way to comprehend how the number of triangles is part of developing the interior angle equation.
Activity Scaling
For lower grades, before the activity, cut an assortment of polygon shapes into triangles. Give teams the cut-outs and challenge them to arrange the triangles into polygons. Then continue with the worksheet.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students take a close look at truss structures, the geometric shapes that compose them, and the many variations seen in bridge designs in use every day. Through a guided worksheet, students draw assorted 2D and 3D polygon shapes and think through their forms and interior angles (mental “testing”) be...

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

Students learn about the fundamental strength of different shapes, illustrating why structural engineers continue to use the triangle as the structural shape of choice.

Simulating a real-world civil engineering challenge, student teams are tasked to create strong and unique truss structures for a local bridge. They design to address project constraints, including the requirement to incorporate three different polygon shapes, and follow the steps of the engineering ...
Copyright
© 2016 by Regents of the University of ColoradoContributors
Maia Vadeen; Malinda Zarske; Nathan Coyle; Ryan Sullivan; Andi Vicksman; Russell Anderson; Sabina SchillSupporting Program
CU Teach Engineering (a STEM licensure pathway), Engineering Plus Degree Program, University of Colorado BoulderAcknowledgements
This activity was developed by CU Teach Engineering, a pathway to STEM licensure through the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.
Last modified: October 19, 2021









User Comments & Tips