Quick Look
Grade Level: 4 (3-5)
Time Required: 30 minutes
Expendable Cost/Group: US $1.50
Group Size: 3
Activity Dependency: None
Subject Areas: Geometry, Physical Science, Problem Solving, Reasoning and Proof, Science and Technology
NGSS Performance Expectations:

| 3-PS2-2 |

Summary
Students use inclined planes as they recreate the difficult task of raising a monolith of rock to build a pyramid. They compare the push and pull of different-sized blocks up an inclined plane, determine the angle of inclination, and learn the changes that happen when the angle is increased or decreased.Engineering Connection
Engineers often incorporate simple machines into their designs of real-world inventions and tools. They use the concept of inclined planes and screws to build useful, strong and durable structures and products. The mechanical advantages of inclined planes may be found in highway access ramps, sidewalk ramps, stairs, escalators, inclined conveyor belts, and switchback roads or trails. Screws are common in everyday applications such as bolts, clamps, fasteners, jar lids, car jacks, spinning stools, spiral staircases, drilling rigs, as well as many types of screws that are designed by engineers for specific purposes.
Learning Objectives
After this activity, students should be able to:
- Identify the different forces acting on an object on an inclined plane.
- Explain how engineers often design things using inclined planes and screws.
- Define and understand inclined plane, friction, work, pull force and screw.
- Describe adjustments they would make to an inclined plane to make the work of moving an object up the plane easier.
- Identify patterns that can be used to predict future motion.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
3-PS2-2. Make observations and/or measurements of an object's motion to provide evidence that a pattern can be used to predict future motion. (Grade 3) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Make observations and/or measurements to produce data to serve as the basis for evidence for an explanation of a phenomenon or test a design solution. Alignment agreement: Science findings are based on recognizing patterns.Alignment agreement: Analyze and interpret data to make sense of phenomena using logical reasoning.Alignment agreement: | The patterns of an object's motion in various situations can be observed and measured; when that past motion exhibits a regular pattern, future motion can be predicted from it. (Boundary: Technical terms, such as magnitude, velocity, momentum, and vector quantity, are not introduced at this level, but the concept that some quantities need both size and direction to be described is developed.) Alignment agreement: | Patterns of change can be used to make predictions. Alignment agreement: |
Common Core State Standards - Math
-
Determine the unknown whole number in a multiplication or division equation relating three whole numbers.
(Grade
3)
More Details
Do you agree with this alignment?
-
Multiply and divide within 100.
(Grade
3)
More Details
Do you agree with this alignment?
-
Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
(Grade
4)
More Details
Do you agree with this alignment?
-
Represent and interpret data.
(Grade
4)
More Details
Do you agree with this alignment?
-
Represent real world and mathematical problems by graphing points in the first quadrant of the coordinate plane, and interpret coordinate values of points in the context of the situation.
(Grade
5)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Design solutions by safely using tools, materials, and skills.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Multiply and divide within 100.
(Grade
3)
More Details
Do you agree with this alignment?
-
Appropriate measurement tools, units, and systems are used to measure different attributes of objects and time.
(Grade
4)
More Details
Do you agree with this alignment?
-
Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
(Grade
4)
More Details
Do you agree with this alignment?
-
Visual displays are used to interpret data.
(Grade
5)
More Details
Do you agree with this alignment?
-
Graph points on the coordinate plane to solve real-world and mathematical problems.
(Grade
5)
More Details
Do you agree with this alignment?
Materials List

Each group needs:
- 1-3 objects, such as a block, toy car, etc. (Note: The cart developed in the hands-on activity in Lesson 3 of this unit is ideal as an object for this activity. The number of objects tested depends on the time available.)
- One wooden board (approximately 40 cm x 20 cm)
- Text books (4 or 5 for stacking)
- Pencil
- Protractor
- Let it Slide! Worksheet
- Spring scale (one per team if available, or share a few among the class; available from science supply catalogs, stores or websites)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_simple_lesson04_activity1] to print or download.Pre-Req Knowledge
General knowledge of pyramids and geometric angles. Familiarity with the six simple machines introduced in Lesson 1 of this unit.
Introduction/Motivation
Today, we will be learning more about a simple machine called an inclined plane. Another name for an inclined plane is a ramp. It can be as simple as the driveway to your house or as complicated as the escalator in a shopping mall. Inclined planes were used in creating the pyramids, to raise the monolith of rock upwards.
If you needed to design an inclined plane to help move gigantic stones to the top of a pyramid, what type of inclined plane would you design? How long would it be? How steep would it be? When we study inclined planes, we think about angles. Angle of inclination is the specific angle between the ground and the inclined plane. For example, if you lean a piece of wood against a house, you create an inclined plane. The slope or angle of steepness of the board rising up is its angle of inclination. When building the pyramids, the angle of inclination had to be considered in creating ramps (inclined planes) to move stones. If the angle of inclination was too big (steep), it would be too hard to push a cart carrying rocks up the ramp. If the angle was too small (shallow), the cart would be easier to push, but it would have to be pushed a longer distance (a very long ramp).

Think about a skateboarding ramp. The steeper the ramp, the more effort it takes to get a skateboard or bicycle up the ramp. If the ramp is shallow, or has a smaller angle of inclination, then it is easier to ride your skateboard or bicycle up the ramp.
Of course, there is always a trade-off. If a ramp has a small angle of inclination, or is shallow, you will not get as far in height as you would with a steep one. You would need to add distance to your ramp to reach a greater height. The trade-off of an inclined plane is distance. You need more distance to move something in a way that takes less effort.
How do we measure how much an inclined plane or simple machine is helping us? Well, we find its mechanical advantage. The greater the mechanical advantage of an object, the smaller the amount of force we need to use to accomplish a task. A good mechanical advantage is greater than 1. For an inclined plane, we find the mechanical advantage by dividing the length of the sloped side of the inclined plane by its height. For example, if you have a ramp that is 2 meters long and it goes up to a height of 1 meter, then you divide 2 meters by 1 meter and get 2. The mechanical advantage of that ramp is 2. A ramp to get an object to the same height with a mechanical advantage of 4 would be easier to move an object up, but would have a smaller angle of inclination, and would be longer.
Through brainstorming, research and hard work, engineers figure out the most effective angle of inclination, considering the trade-offs between the amount of work needed and the distance an object is moved up the inclined plane. Through the experimentation in this activity, we are going to look at see the difference in amount of work needed when we change the angle of inclination. We can use this information to understand why engineers use inclined planes today and how inclined planes may have been designed to drag big stones to the top of pyramids in ancient times.
Procedure
Before the Activity
- Gather materials and make copies of the Let it Slide! Worksheet.
- Designate testing areas for the inclined planes.
With the Students
- Divide the class into teams of three students each. Distribute one worksheet per team.
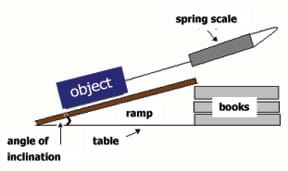
- Model for the students how to conduct a test by setting the inclined plane to the first angle of inclination on the worksheet using stacked textbooks, measuring the object's mass, and pulling the object up the inclined plane using the spring scale. See Figure 1.
- Explain the steps that they will complete for each test object.
- Use your protractor and books to set your board at a 15-degree angle from the table or desk. This creates a 15-degree inclined plane.
- Hook the object to the spring scale.
- Pull the object up the inclined plane.
- Record the spring scale measurement (in grams).
- Add more books to make your inclined plane form the next angle in the worksheet chart.
- Repeat these steps for all the degrees of inclined planes listed in the chart.
- Before beginning, challenge each student to predict the results for different blocks, angles and floors.
- Have students gather the materials for their projects.
- Have students determine the mass of their objects. As they attach the different blocks to the spring scale, they can feel and see the difference in required force that will be required to move the blocks up the inclined plane.
- Have students follow along the activity with the worksheet, answering the questions.
- Have students calculate the mechanical advantage of an inclined plane by completing the Math Application problems described in the Assessment section. Write on the board: Mechanical advantage of an inclined plane = length of slope ÷ height of plane.
- Conclude the activity with a comparison of team results and a discussion on inclined planes. Which angle made pulling the object easier? (Answer: The smaller the angle, the easier to pull the object or the less force measured on the spring scale.) What is the trade off of a smaller angle? (Answer: Distance) Do you think inclined planes or ramps made pulling large bocks of stone to the top of a pyramid easier? (Answer: Yes) If you were an engineer hired in ancient times to build a pyramid, what type of inclined plane would you use to get the large blocks to the top? (Answer: Varies, but the easiest way to get the stones up would be a longer, shallow ramp.) How do modern day engineers use inclined planes to help make work easier? (Answer: They design conveyer belts, ramps and escalators that move objects with a greater mechanical advantage.)
Vocabulary/Definitions
angle of inclination: The angle on the bottom of the ramp, formed by the ramp and a horizontal line (see Figure 1).
friction: The force that resists motion between two bodies in contact.
inclined: Sloping, slanting or leaning. To deviate from the horizontal.
inclined plane: A simple machine that raises an object to greater height. Usually a straight slanted surface and no moving parts, such as a ramp, sloping road or stairs.
mechanical advantage : An advantage gained by using simple machines to accomplish work with less effort. Making the task easier (which means it requires less force), but may require more time or room to work (more distance, rope, etc.). For example, applying a smaller force over a longer distance to achieve the same effect as applying a large force over a small distance. The ratio of the output force exerted by a machine to the input force applied to it.
monolith: A large block of stone, especially one used in architecture or sculpture.
pull force: Cause of motion or change.
ramp: An inclined surface or roadway connecting different levels.
screw: A simple machine that lifts or holds materials together. Often a cylindrical rod incised with a spiral thread.
simple machine: A machine with few or no moving parts that is used to make work easier (provides a mechanical advantage). For example, a wedge, wheel and axle, lever, inclined plane, screw, or pulley.
slope: An inclined line, surface, plane, position or direction. The amount or degree of deviation from the horizontal.
spiral: A curve that winds around a fixed center point (or axis) at a continuously increasing or decreasing distance from that point.
work: Force on an object multiplied by the distance it moves. W = F x d (force multiplied by distance).
Assessment
Pre-Activity Assessment
Know / Want to Know / Learn (KWL) Chart: Create a classroom KWL chart to help organize learning about a new topic. On a large sheet of paper or on the classroom board, draw a chart with the title "Simple Machines: Inclined Planes and Screws." Draw three columns titled, K, W and L, representing what students know about inclined planes and screws, what they want to know about inclined planes and screws and what they learned about inclined planes and screws and their mechanical advantages. Fill out the K and W sections during the lesson introduction as facts and questions emerge. Fill out the L section at the end of the lesson.
Activity-Embedded Assessment
Worksheet: Observe the students as they complete the Let it Slide! Worksheet. Is each student actively engaged? Review their answers to gauge their mastery of the subject.
Patterns: Have students identify any patterns they observe about the motion of the object's motion at the different incline angles. Have them share how that can be used to predict future motion.
Post-Activity Assessment
KWL Chart (Conclusion): As a class, finish column L of the KWL Chart as described in the Pre-Lesson Assessment section. List all of the things students learned about inclined planes and screws and their mechanical advantages. Were all of the W questions answered? What new things did they learn?
Engineering Pyramid Design: Have the students draw a picture of their ramp, which could be used to help pyramid engineers get large stones to the top of a pyramid. Is their inclined plane long or short, steep or shallow? Allow students to be creative with their designs and show how the stones will be moved up the inclined plane.
Graphing Application: Discuss as a class how the angle of the inclined plane affects the force required to pull the mass up the plane. Create a graph of angle vs. force for a visual representation.
Math Application: To determine the mechanical advantage of an inclined plane, divide the length of the slope of the plane by the height of the inclined plane. Have students solve the following problems about the mechanical advantage of an inclined plane:
What is the mechanical advantage of the following inclined planes?
- An inclined plane with a sloping side of 2 meters long and a height of 1 meter? (Answer: 2 ÷1 = 2, so the mechanical advantage of the inclined plane is 2.)
- An inclined plane with a sloping side of 6 meters long and a height of 3 meters? (Answer: 6 ÷ 3 = 2, so the mechanical advantage of the inclined plane is 2.)
- An inclined plane with a sloping side of 10 meters long and a height of 2 meters? (Answer: 10 ÷ 2 = 5, so the mechanical advantage of the inclined plane is 5.)
- An inclined plane with a sloping side of 4 meters long and a height of 4 meters? (Answer: 4 ÷ 4 = 1, so the mechanical advantage of the inclined plane is 1.)
Now, answer the following questions:
- Which inclined plane is the longest? (Answer: Inclined plane in problem 3.)
- Which inclined plane has the greatest mechanical advantage? (Answer: Inclined plane in problem 3.)
- Which inclined plane is the shortest? (Answer: Inclined plane in problem 1.)
- Which inclined plane has the least mechanical advantage? (Answer: Inclined plane in problem 4.)
- Does a longer the inclined plane make a mechanical advantage greater? (Answer: Yes)
- Does a greater mechanical advantage make work easier? (Answer: Yes)
In conclusion, the longer the inclined plane, the easier to move an object. The trade-off is distance.
Troubleshooting Tips
It helps students if the teacher first demonstrates how to pull the objects up the inclined plane.
Reiterate the importance of using protractors to measure the angles. This is a tested skill and practicing it in this activity is a great opportunity.
Activity Extensions
Using the same activity setup, have students study how friction affects the work on an inclined plane by having them lay down on their ramps strips of carpet or sand paper, or another material that affects the friction. Ask them to explain why the block is harder or easier to pull up.
Using the same activity setup, have students roll balls down their ramps to demonstrate the use of an inclined plane to study friction instead of work. Roll balls with different masses down the ramp, and use a stopwatch to time how long it takes the balls to reach the bottom. Use different surfaces than the wooden board to affect the friction of the inclined plane.
Activity Scaling
- For younger students, consider having the four stations with each angle/inclined plane already set up. Have the students rotated through the stations and just practicing how to use a spring scale to measure. For more advanced younger students, test only one object as the angle of the inclined plane changes, instead of three. Help them use a protractor, as necessary.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students explore building a pyramid, learning about the simple machine called an inclined plane. They also learn about another simple machine, the screw, and how it is used as a lifting or fastening device.

Students are introduced to the six types of simple machines — the wedge, wheel and axle, lever, inclined plane, screw, and pulley — in the context of the construction of a pyramid, gaining high-level insights into tools that have been used since ancient times and are still in use today.

This lesson introduces students to three of the six simple machines used by many engineers. These machines include the inclined plane, the wedge and the screw.

Students are introduced to the concept of simple tools and how they can make difficult or impossible tasks easier. They begin by investigating the properties of inclined planes and how implementing them can reduce the force necessary to lift objects off the ground.
References
Dictionary.com. Lexico Publishing Group, LLC. Accessed January 25, 2006. (Source of some vocabulary definitions, with some adaptation) http://www.dictionary.com
Henderson, Tom. Lesson 3: Forces in Two Dimensions: Inclined Planes. The Physics Classroom (a high school physics tutorial). Accessed January 25, 2006. http://www.compadre.org/precollege/items/detail.cfm?ID=2014
Wright, Richard. Ladies and gentleman... the inclined plane! PCS Education Systems, Inc. Accessed January 25, 2006. http://www.weirdrichard.com/inclined.htm
Copyright
© 2005 by Regents of the University of Colorado.Contributors
Travis Reilly; Glen Sirakavit; Malinda Schafer Zarske; Lawrence E. Carlson; Jacquelyn F. Sullivan; Denise W. Carlson, with design input from the students in the spring 2005 K-12 Engineering Outreach Corps course.Supporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education, and National Science Foundation GK-12 grant no 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 13, 2025








User Comments & Tips