Quick Look
Grade Level: 6 (5-7)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 This activity uses some non-expendable (reusable) items, such as smartphone video cameras and LEGO EV3 components and software; see the Materials List for details.
Group Size: 3
Activity Dependency: None
Subject Areas: Measurement, Physical Science, Science and Technology
NGSS Performance Expectations:

| 5-ESS2-1 |
| MS-ESS2-5 |
Summary
Students learn about the Foucault pendulum—an engineering tool used to demonstrate and measure the Earth's rotation. Student groups create small experimental versions, each comprised of a pendulum and a video camera mounted on a rotating platform actuated by a LEGO® MINDSTORMS® EV3 motor. When the platform is fixed, the pendulum motion forms a line, as observed in the recorded video. When the rotating, the pendulum's motion is observed as a set of spirals with a common center. Observing the patterns that the pendulum bob makes when the platform is rotating provides insight as to how a full-size Foucault pendulum operates. It helps students understand some of the physical phenomena induced by the Earth's rotation, as well as the tricky concept of how the perception of movement varies, depending on one's frame of reference.Engineering Connection
Students get a taste of mechanical engineering and computer science, first by building a rotating chassis to carry a video camera and mounting a pendulum on a fixed support, then by running (provided) software programs from the LEGO EV3 brick to control the rotating chassis motion. Then they compare the fixed vs. in-motion camera video recordings of the pendulum movement in order to make an analytical inference, similar to what practicing engineers do. The rotation of the Earth plays a pervasive role in the natural phenomena of our world, and hence in science and engineering. The Earth's rotation causes the Coriolis effect, and the rate of rotation is taken into consideration by engineers who examine wind patterns and ocean currents, make weather prediction models, study long-range projectile motion, and plan flight paths and launch rockets (trajectories).
Learning Objectives
After this activity, students should be able to:
- Relate the effect of the Earth's rotation to the formation and movement of winds such as typhoons and cyclones.
- Explain why engineers must take into consideration the Earth's rotation when designing and launching missiles.
- Describe how a Foucault pendulum is used to exhibit and measure the Earth's rotation.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Science explanations describe the mechanisms for natural events.
(Grade 5)
More Details
Do you agree with this alignment?
| NGSS Performance Expectation | ||
|---|---|---|
|
5-ESS2-1. Develop a model using an example to describe ways the geosphere, biosphere, hydrosphere, and/or atmosphere interact. (Grade 5) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop a model using an example to describe a scientific principle. Alignment agreement: | Earth's major systems are the geosphere (solid and molten rock, soil, and sediments), the hydrosphere (water and ice), the atmosphere (air), and the biosphere (living things, including humans). These systems interact in multiple ways to affect Earth's surface materials and processes. The ocean supports a variety of ecosystems and organisms, shapes landforms, and influences climate. Winds and clouds in the atmosphere interact with the landforms to determine patterns of weather. Alignment agreement: | A system can be described in terms of its components and their interactions. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ESS2-5. Collect data to provide evidence for how the motions and complex interactions of air masses results in changes in weather conditions. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Collect data to produce data to serve as the basis for evidence to answer scientific questions or test design solutions under a range of conditions. Alignment agreement: | The complex patterns of the changes and the movement of water in the atmosphere, determined by winds, landforms, and ocean temperatures and currents, are major determinants of local weather patterns. Alignment agreement: Because these patterns are so complex, weather can only be predicted probabilistically.Alignment agreement: | Cause and effect relationships may be used to predict phenomena in natural or designed systems. Alignment agreement: |
Common Core State Standards - Math
-
Represent and interpret data.
(Grade
5)
More Details
Do you agree with this alignment?
-
Convert like measurement units within a given measurement system.
(Grade
5)
More Details
Do you agree with this alignment?
-
Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
(Grade
6)
More Details
Do you agree with this alignment?
-
Summarize numerical data sets in relation to their context, such as by:
(Grade
6)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the effects of technology on the environment.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Represent and interpret data.
(Grade
5)
More Details
Do you agree with this alignment?
-
Convert like measurement units within a given measurement system.
(Grade
5)
More Details
Do you agree with this alignment?
-
Summarize numerical data sets in relation to their context, such as by:
(Grade
6)
More Details
Do you agree with this alignment?
-
Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.
(Grade
6)
More Details
Do you agree with this alignment?
New York - Science
-
Develop a model using an example to describe ways the geosphere, biosphere, hydrosphere, and/or atmosphere interact.
(Grade
5)
More Details
Do you agree with this alignment?
-
Collect data to provide evidence for how the motions and complex interactions of air masses results in changes in weather conditions.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
Materials List
Each group* needs:
- pendulum, composed of soft string, a bob (a heavy object) and a fixed support structure (tripod, table or chair) to which the string is tied (or tied to a screw attached to the support structure)
- video camera, such as the camera in a smartphone or tablet; alternatively, use a wireless camera (although more expensive)
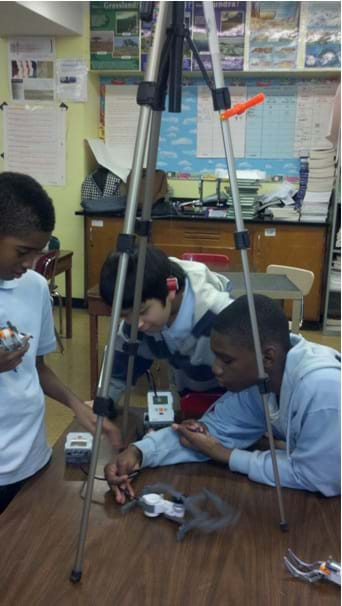
- turntable platform to hold and rotate the video camera, assembled from LEGO components, as shown in the Experimental Setup Build Photos (and Figures 1, 6 and 7); LEGO components include a servo motor connected to an intelligent brick, plus chassis, axle, wheel and a gear where the chassis is mounted; alternatively, use some other device capable of rotating the camera
- LEGO EV3 Servo Motor, available at http://shop.lego.com/en-US/EV3-Large-Servo-Motor-45502
- LEGO MINDSTORMS EV3 Intelligent Brick, available at http://shop.lego.com/en-US/EV3-Intelligent-Brick-45500
- Foucault Pendulum Pre-Activity Survey, one per person
- Foucault Pendulum Worksheet, one per person
- Foucault Pendulum Post-Activity Survey, one per person
*If only one LEGO EV3 brick is available, share the brick among teams, or build only one Foucault pendulum and turntable experimental setup and conduct the activity as a class demonstration.
To share with the entire class:
- LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-EV3-core-set-/5003400
- LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first; at https://www.lego.com/en-us/mindstorms/downloads/download-software
- computer, loaded with EV3 1.2.1 software, and three provided LEGO programs installed: servo_control_speed1.ev3, servo_control_speed2.ev3 and servo_control_speed3.ev3
- USB cable
- projector to show the class the Visual Aid and video clips recorded during the experiments
- larger pieces of paper and tape, onto which tracings can be made from the projected videos
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- LEGO MINDSTORMS Education NXT Software 2.1
- computer, loaded with NXT 2.1 software, and three provided LEGO programs installed: servo_control_speed1.rbt, servo_control_speed2.rbt and servo_control_speed3.rbt
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_foucault_activity1] to print or download.Introduction/Motivation
When watching the weather on television, have you ever noticed that tropical storms such as hurricanes, typhoons and cyclones, form spiral-shaped patterns? (See Figure 2.) Do you know that guiding fast-moving objects over long distances, such as airplanes and rockets, requires pilots or navigators to take into account the Earth's rotation? (Allow time for student response, input and engagement.)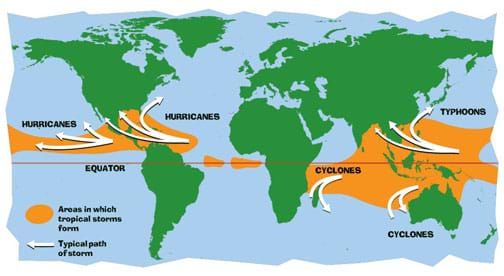
This is due to something called the "Coriolis effect," which is also responsible for trade winds, and some ocean currents. (See if any students have heard of the Coriolis effect or trade winds).
The Coriolis effect describes the apparent motion of an object from a rotating frame of reference. This apparent motion is caused by the Coriolis force, which is known as an inertial force or fictitious force, because it only occurs within a rotating frame of reference; this means it does not exist at all if the object's motion is observed from a stationary position. The Coriolis force acts perpendicular to the direction of motion of the object and to the axis of rotation of the frame of reference. It acts on a mass, such as wind (remember that air has mass!) or an airplane or rocket.
Listen to this description of the Coriolis effect from the National Geographic magazine:
The key to the Coriolis effect lies in the Earth's rotation. The Earth rotates faster at the equator than it does at the poles. This is because the Earth is wider at the equator. A point on the equator has farther to travel in a day.
Let's pretend you are standing at the equator and you want to throw a ball to your friend in the middle of North America. If you throw the ball in a straight line, it will appear to land to the right of your friend because he's moving slower and has not caught up.
Now let's pretend you're standing at the North Pole. When you throw the ball to your friend, it will again appear to land to the right of him. But this time, it is because he's moving faster than you are and has moved ahead of the ball.
This apparent deflection is the Coriolis effect. The wind is like the ball. It appears to bend to the right in the Northern Hemisphere. In the Southern Hemisphere, winds appear to bend to the left. 
On Earth, which is a rotating reference frame, the effect is important in the formation of cyclonic weather events such as tornadoes and hurricanes. (Make sure students know about the Earth's tilted rotation on its axis.) These cyclonic weather events are deflected to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. Since the equator is furthest from the Earth's axis of rotation, it is the fastest moving region. This provides insight as to why the equator is a common place for cyclones and hurricane formations, and also for rocket and intercontinental missile launching pads (see Figure 3).
Now, imagine that you an engineer working at NASA and you are involved in the next big rocket launch. A rocket is a fast-moving object and you would likely use a computer to guide it. In order to calculate the rocket's trajectory to upload into the computer, you must take into account the rate at which Earth spins. Failing to do so might cause the rocket to miss its trajectory and the rocket launch would be a failure.
As another example, the weather prediction models designed by engineers must take into consideration the Earth's rotation so that meteorologists can use the models to accurately predict wind and storm paths in advance of their arrivals. Accurate prediction gives us a chance to alert people that big storms are coming.
How can we measure how fast the Earth is spinning if we are standing on it? How can we, as engineers, account for the Coriolis effect? (Listen to student ideas.)
This is a tricky question that has challenged the minds of great scientists through the centuries. The answer comes from an engineered tool developed in the 1850s by a French physicist and engineer named Leon Foucault. Foucault traced the motion of a pendulum that moves in a perfectly straight line in the absence of the Earth's rotation in order to accurately measure how fast the Earth is spinning (see Figure 4).
In practice, to observe the Coriolis effect using Foucault's method requires several days of observation. During our experiment, we will reproduce a similar, smaller experimental setup that illustrates how this method works, but in a much faster time frame. We can do this thanks to some technological tools developed by engineers, items such as microcontrollers, smartphones and tablet computers.
Two branches of engineering are related to what we do in this activity. You'll get a taste of:
- mechanical engineering with the design and construction of a pendulum, and
- computer engineering with the software program to rotate the platform supporting the camera.
In addition, we will use our math skills to determine the relationship between the speed of the spinning camera and the number of spirals observed.
Procedure
Background
The rotation of the Earth plays a pervasive role in the natural phenomena of our world, and hence in science and engineering. The Earth's rotation causes the Coriolis effect, and the rate of rotation must be taken into consideration by engineers who examine wind patterns and make weather prediction models, study long-range projectile motion, plan flight paths and launch rockets. For example, a long-range projectile launched along a longitudinal line undergoes an apparent deflection due to the Earth's rotation. The prediction of wind and storm paths (cyclones, typhoons, etc.) would be inaccurate if the Coriolis effect was not included in the trajectory calculations. Accurately measuring the Earth's rate of rotation has challenged the greatest scientific minds, including Sir Isaac Newton. The Foucault pendulum is the most well-known engineered tool for estimating the Earth's rotation.
Before the Activity
- Gather materials and make copies of the Foucault Pendulum Pre-Activity Survey, Foucault Pendulum Worksheet and Foucault Pendulum Post-Activity Survey, one each per student.
- As homework before the activity, give each student a three-question pre-activity survey to complete and return to you in advance of the activity, as described in the Assessment section.
- It may be helpful to make copies of the Experimental Setup Build Photos (contains Figures 1, 6 and 7), one per team, as a handy reference for when groups build their experimental setups.
- Install the EV3 software on the computer. Also install the three provided LEGO programs—servo_control_speed1.ev3, servo_control_speed2.ev3 and servo_control_speed3.ev3—in anticipation of students uploading them to the EV3 bricks.
- Prepare to show the class the Visual Aid, which is composed of Figures 2, 3 and 5), by overhead projector. Have ready the ability to play back to the class the recorded videos, perhaps on a computer monitor or projected on a classroom board or wall.
With the Students
- Lead an informal discussion to review the pre-activity survey answers, as described in the Assessment section.
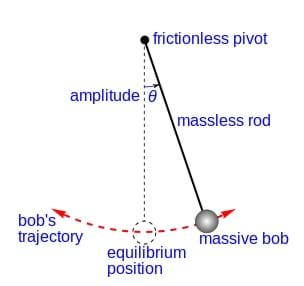
Figure 5. An ideal model of a simple gravity pendulum. - Introduce the simple pendulum and the coordinates system. To introduce the simple pendulum, project the simple pendulum visual aid (Figure 5), describe the pendulum components and explain the motion in the relation with the gravity of the bob moved from its resting position. Explain that the Cartesian coordinates system in a plane comprises two axes, x and y, which are perpendicular and have a common origin. In a coordinate system any position in the plane is uniquely determined. To illustrate, draw a Cartesian coordinate grid with the projected image of the pendulum, centering the equilibrium point of the bob; then ask students to determine the coordinates of the bob at angle theta.
- Present the Introduction/Motivation section content to introduce the Coriolis effect and Foucault pendulum. As part of this, show the visual aid for Figure 2 to illustrate the deflection of winds to the right in the Northern Hemisphere and to the left in the Southern Hemisphere due to the Earth's rotation. Mention the similar effect observed with rocket and ballistic missiles, and the location of the space shuttle launch pad (Figure 3).
- Divide the class into groups of three students each. Hand out the worksheets for students to complete as they conduct their experiments.
- Have each group prepare its pendulum by attaching a bob to the string and mounting the string so it hangs freely from a fixed support, such as a tripod, table or chair. Fix the string to the support directly or via a screw. The setup is shown in Figure 1.

Figure 6. Make a turntable mechanism to rotate a camera to record an oscillating pendulum. - Have each group assemble its LEGO turntable platform, as shown in Figures 6 and 7, or use any other device capable of rotating a smartphone or tablet. The turntable is composed of a motor connected to a LEGO brick, chassis, axle, wheel and a gear where the chassis is mounted. Refer to the build photos and Figures 1, 6 and 7.
- Have students securely mount or attach their cameras to the top of their turntables (see Figure 6). Connect the motor to the EV3 brick and use the computer to upload the, servo_control_speed1.ev3 program to the brick.

Figure 7. Various views of the LEGO turntable mechanism: (top left) base attached to a LEGO servo motor and resting on the floor; (top right) the entire turntable; (bottom left) underside view of the camera support; (bottom right) top view of the camera support. - Initiate the pendulum motion by moving it to a small angle from the vertical position; initiate the turntable by running the program on the EV3 brick.
- First, have students record on their worksheets the motion of the pendulum from a stationary camera. In the recorded video, expect the observed motion to be a straight line (as most students should have guessed after the introduction).

Figure 8. The path traced by a Foucault pendulum. - Next, ask students to hypothesize what the motion of the pendulum will look like from a rotating platform.
- Have students perform the experiment again, rotating the camera by running the LEGO EV3 program. The platform must be rotated at a very low speed between powers 5 to 15, depending on how fast the pendulum is moving. While recording, make sure the pendulum bob stays visible to the camera lens at all times.
- After recording, display the video on a computer or project it on a board and have students trace the path of the pendulum on a sheet of paper (see Figure 8). Repeat this procedure for different turntable speeds by uploading and running the servo_control_speed2.rbt and servo_control_speed3.ev3 programs. The speed is adjusted in the program via computer and the LEGO software by clicking on the move block and changing the motor power.
- Have students discuss their results and observations, first in their groups, and then as a class, relating the rotation of the camera to an object on the Earth's surface. Have them think about the effects of such rotation for an object not lying on the Earth's surface, for example, if an object is floating in the air and moving.
Vocabulary/Definitions
ballistics: The study of the motion of projectiles; flight dynamics; the trajectory of an object in free flight.
coordinates: A number that identifies a position relative to an axis.
Coriolis effect: The effect that describes the apparent motion of an object observed from a rotating frame of reference.
Foucault pendulum: An engineering tool comprised of a simple pendulum that is used to demonstrate and measure the Earth's rotation.
pendulum: A weight suspended from a fixed point so as to be able to swing freely.
rotation: The circular movement of an object about an axis.
Assessment
Pre-Activity Assessment
Pre-Activity Survey: Assign as pre-activity homework the three-question Foucault Pendulum Pre-Activity Survey for students to complete before the class period when the activity is conducted. Collect and review students' answers to gauge their baseline understanding of the subject matter and assist you in guiding the discussion and explanations during the activity.
Informal Discussion: To begin the activity, ask students some questions about the subject matter, covering the pre-survey answers provided in the Foucault Pendulum Pre-Activity Survey Answers. Ask:
- What is a pendulum? Where have you seen one used?
- What have you heard about Earth's rotation?
- What might we use to illustrate and measure the Earth's rotation?
Activity Embedded Assessment
Analysis: While the experiments are being conducted, have students complete the Foucault Pendulum Worksheet by recording data, and observing and drawing patterns. Ask students to comment on what they observe while the motor is fixed and when the motor is rotating. Review students' worksheet answers, plots and inferences to gauge their comprehension.
Post-Activity Assessment
Discussion: Ask students to comment on how they could use their understanding of the Earth's rotation as learned in this activity if they were engineers. Have students write their ideas on the back of the worksheet and then share and discuss their answers as a class.
Post-Activity Survey: Hand out the five-question Foucault Pendulum Post-Activity Survey for students to complete as homework. Review their answers to assess their comprehension of the activity concepts.
Troubleshooting Tips
Verify that the equipment is set up correctly, the battery is charged and the motor is correctly connected to the EV3 brick.
Make sure the servo_control_speed1.ev3, servo_control_speed2.ev3, servo_control_speed3.ev3 are running.
The operating instructions for the LEGO MINDSTORMS EV3 are provided with the core set. Refer to the EV3 website for any other issues: https://www.lego.com/en-us/mindstorms/support/
Activity Scaling
For lower grades:
- Provide more in-depth explanations of trade winds, pendulums, etc. Make sure students know about the rotation of the Earth, the Earth's axis and the equator.
- Conduct the activity as a class demonstration, or in larger groups.
- Work through the activity slowly, with more explanations throughout. Focus more on vocabulary and review prior to conducting the activity.
For upper grades, have students find other relationships to the Coriolis effect apart from the examples given in class (trade winds and rocket projections).
Additional Multimedia Support
Show students an animation of the Coriolis effect at
http://commons.wikimedia.org/wiki/File:Corioliskraftanimation.gif.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn what causes hurricanes and what engineers do to help protect people from destruction caused by hurricane winds and rain.

Students are introduced to the ways that engineers study and harness the wind. They learn about the different kinds of winds and how to measure wind direction. In addition, they learn how air pressure creates winds and how engineers design and test wind turbines to harness renewable wind energy.

The purpose of this lesson is to teach students how a spacecraft gets from the surface of the Earth to Mars. Students first investigate rockets and how they are able to get us into space. Finally, the nature of an orbit is discussed as well as how orbits enable us to get from planet to planet — spec...

Students are introduced to natural disasters and learn the difference between natural hazards and natural disasters.
References
Baker, Gregory L. and James A. Blackburn. "The Pendulum. A Case Study in Physics." AMC 10 (2005): 12.
Braginsky, Vladimir B., Aleksander G. Polnarev, and Kip S. Thorne. "Foucault Pendulum at the South Pole: Proposal for an Experiment to Detect the Earth's General Relativistic Gravitomagnetic Field." Published August 27, 1984. Physical Review Letters 53.9 (1984): 863-866. http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.53.863
Coriolis effect. Encyclopedic Entry, Reference and News, Education, National Geographic. Accessed April 16, 2014. http://education.nationalgeographic.com/education/encyclopedia/coriolis-effect/?ar_a=1
Hart, John B., Raymond E. Miller and Robert L. Mills. "A Simple Geometric Model for Visualizing the Motion of a Foucault Pendulum." Published January 20, 1986. American Journal of Physics 55.1 (1987): 67-70. http://scitation.aip.org/content/aapt/journal/ajp/55/1/10.1119/1.14972
Copyright
© 2014 by Regents of the University of Colorado; original © 2012 Polytechnic Institute of New York UniversityContributors
Violet Mwaffo and Jeffrey Laut, NYU Polytechnic School of EngineeringSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020









User Comments & Tips