Hands-on Activity The Balancing Act

Learning Objectives

After this activity, students should be able to:

• Explain the principle idea of a "balanced" equation.
• Balance and solve one- or two-step algebraic equations.
• Describe the purpose and usage of a LEGO MINDSTORMS EV3 Intelligent Brick and sensors (especially a color sensor).

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) for at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
• set of gram masses

To share with the class:

• Additional LEGO bricks for balancing scale construction; suggested purchase: LEGO Fun with Bricks set containing 600 pieces
• LEGO MINDSTORMS Software, available for download at https://education.lego.com/en-us/downloads/mindstorms-ev3/software, with instructions for installing the software

Alternative: LEGO MINDSTORMS NXT Set:

Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:

• LEGO MINDSTORMS NXT robot, such as NXT Base Set
• computer loaded with the NXT 2.1 software

Worksheets and Attachments

Pre-Req Knowledge

• A familiarity with the use of addition, subtraction, division and multiplication manipulation of integers within algebraic expressions.
• A beginner's understanding of one-variable algebraic equations.

Introduction/Motivation

Entering into the world of the unknown can be a daunting experience; however it's not an avoidable experience! You have all been introduced to the world of the unknown when you were first introduced to the world of algebra. That's where we use letters and symbols to represent unknown quantities and numbers in mathematical statements known as equations. Understanding how to use and solve for these algebraic equations is a vital skill for everyone at any level of occupation, and not just engineers and scientists. However, in the beginning, algebra can be discouraging from frustration that sometimes occurs with learning and practicing algebra and complex math.

An equation is any mathematical statement that expresses two quantities to be equal indicated by an equal sign "=". For instance, the number of apples = the number of oranges is an example of a basic equation. Or perhaps, Temperature = yesterday's temperature + 5 °C. You might recognize Einstein's most famous equation, E = mc², known as mass-energy equivalence formula. The phenomenon of this equation is beyond the scope of our activity, but it brings home the point that even Einstein utilized a basic form of an equation!

Equations are typically seen in the form similar to 3x + 2 = 5, where "x" indicates an unknown value or quantity known as the variable, "3" is the coefficient of x, "2" and "5" are constants that are represented as known quantitative values, and "+" is a mathematical operator. The "=" sign states items on the right and left side of the = sign are equivalent. One key note, if a quantity is not a constant, then it is a variable.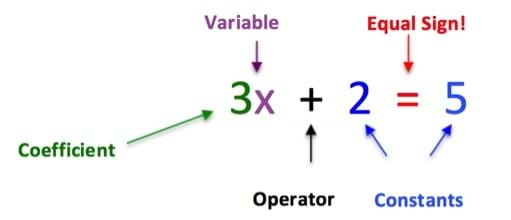

In this activity, we will use an interactive method in which you will be able to practice what you've learned about solving algebraic equations through the literal sense of what it means to be an equation: to be equal, to be balanced. The main goal for solving algebraic equations is to get the variable on one side of the equal sign by itself (that is,. x = some number). To eliminate a term on one side of the equation, you must use the opposite mathematical operation known as the inverse operation. This technique is typically taught as: Whatever you do to one side of the equation, you must do to the other side in order to keep the equation balanced. The easiest way to solidify this concept is to think of a balancing scale.

If you were to add weight to one side of the balance scale, you must add weight to other side of the balance scale in order to keep it balanced and leveled!

If you were to only add weight to only one side of the balance scale, the balance scale will lean to one side and it becomes imbalance, as shown below!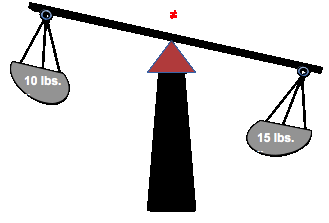

The same thing goes for equations. If you change one side of the equation, you must make the same equal change to the other side of the equation in order for the equation to remain balanced and equal! Here's an example of solving the equation x + 2 = 5, shown in Figures 1 - 5. You must first subtract 2 from the right side of the equal sign and then do exactly the same operation to the left side of the equal sign. The end results you'll get is x = 3.

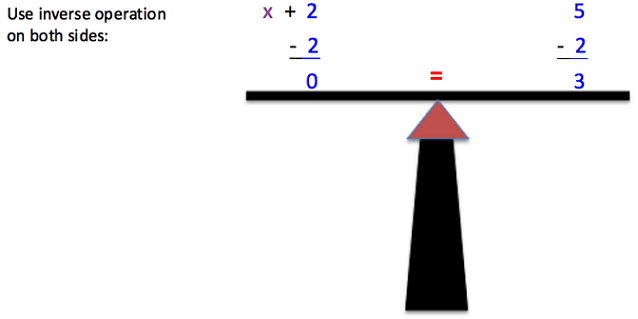
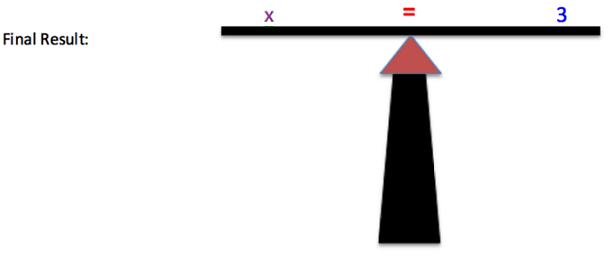
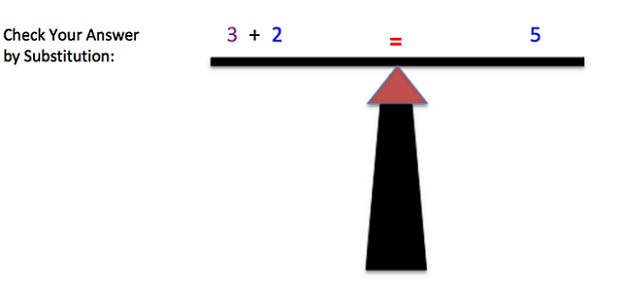
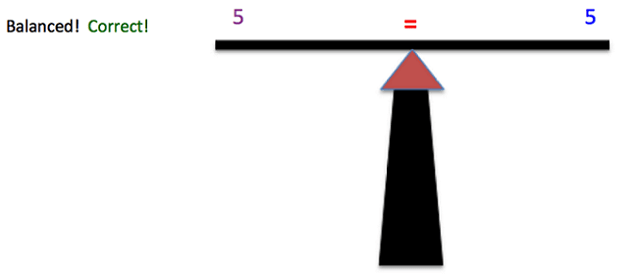
Always check your answer by substituting the value back into the original equation and verifying that the quantities on both side of the equation are equaled, and thus, balanced!

The above example is an example of a one-step equation. A one-step equation is literally an equation that takes one step to solve. A two-step equation is literally an equation that takes two steps to solve. In the activity today, we will be practicing both types of these equations and checking your answers using a balance scale built using the LEGO MINDSTORMS EV3 parts, LEGO pieces and mass weights. We will represent unknown variables using a LEGO EV3 Intelligent Brick and constants using multiples of 1, 5, 10 or 20-gram masses. For instance, a constant valued as 5 will be represented using a 5 gram mass.

Procedure

Background

PARTS TO KNOW:

The pieces that are used on the LEGO Balance Scale are shown in Figure 6. The gram masses can be labeled with a marker or paint to show which ones represent positive constants and which ones represent negative constants.

The LEGO Balance Scale is constructed before the activity begins. Figure 7 shows illustrations of the balance scale with and without a Balance Indicator. The color sensor is built into the balance scale's tower and hidden behind the Balance Indicator. The Balance Indicator's black and yellow LEGO blocks are used in order for the color sensor to detect dark (black blocks) and light (yellow blocks) variations when the scale is balanced or imbalanced when the scale sways up and down to reach equilibrium. The color sensor will see yellow when the scale is balanced and leveled horizontally, otherwise the color sensor will see black when the scale is imbalanced and unleveled horizontally.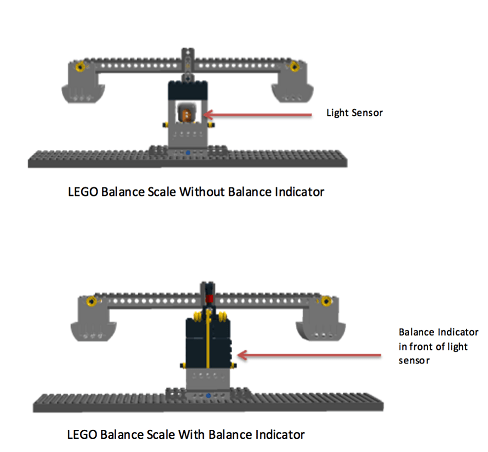

The necessary components from the LEGO MINDSTORMS EV3 includes programmable EV3 intelligent brick; 3 interactive servo motors; sound, color, ultrasonic and 2 touch sensors; and many other components and instructions. The LEGO Programmable EV3 Brick is used for programming the color sensor interaction with the LEGO Balance Scale. The color sensor is used to determine balance and imbalance detected on the scale, and the basket container is used to store masses and LEGO variable and constant pieces (see Figure 8) .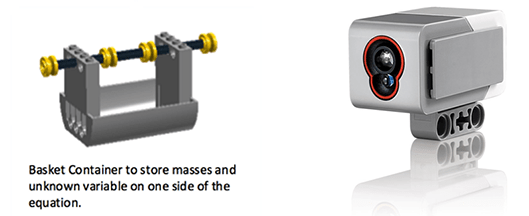

HOW IT WORKS:

Using a new example, 3x - 2 = 4, Figures 9 - 17 explain how to use the LEGO Balance Scale to solve for the unknown variable x.

Configure the equation onto the LEGO Balance Scale, shown in Figure 9. Note that since we have not solved for x and do not know its true value, the LEGO Balance Scale is initially unbalanced.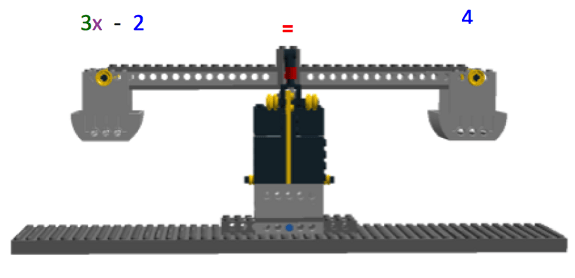

Figure 10 shows the LEGO pieces and the gram masses that represent the different terms in the equation 3x – 2 = 4.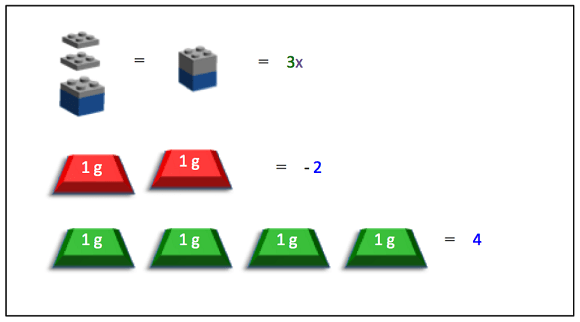

Once all the LEGO pieces and gram masses for representing the equation components have been determined and gathered, they should be assembled on the LEGO Balance Scale, as shown in Figure 11.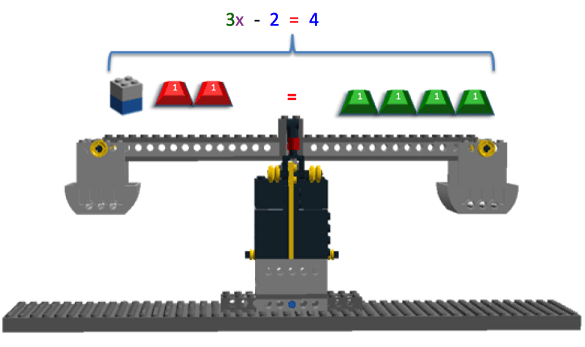

The next step is to represent the inverse operation needed to cancel out the "-2," which is to add a constant value of 2 to both sides of the equation. Therefore, two positive 1g masses are added to each side of the equation. On the left side, this cancels out the "-2." so both the two negative 1g masses and the two positive 1g masses are removed from the left side of the scale. This process is illustrated in Figures 12 and 13.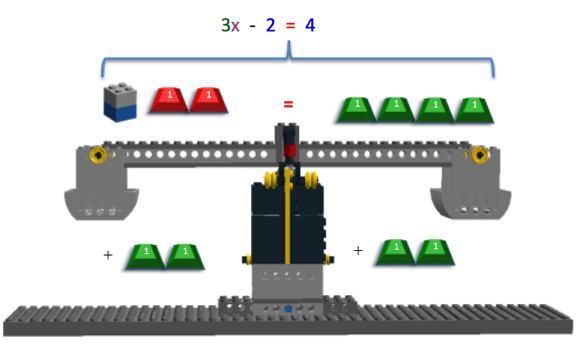

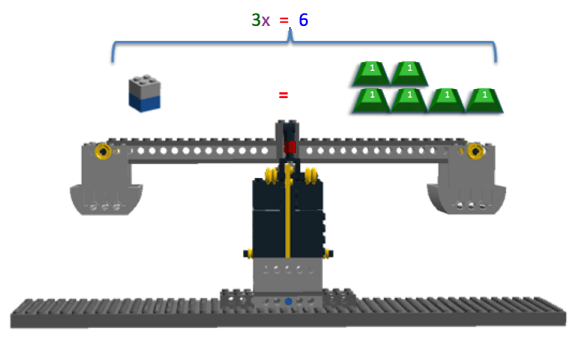
One last step must be performed to solve for x. Since x is multiplied by 3 in the equation 3x = 6, both sides of the equation need to be divided by 3, which is the inverse operation of multiplied by 3. On the left side, multiplying and dividing by 3 cancel out, leaving only x represented by the LEGO brick. On the right side of the equation, 6 is divided by 3, leaving the value of 2 represented by two positive 1g masses. This step is shown in Figure 14.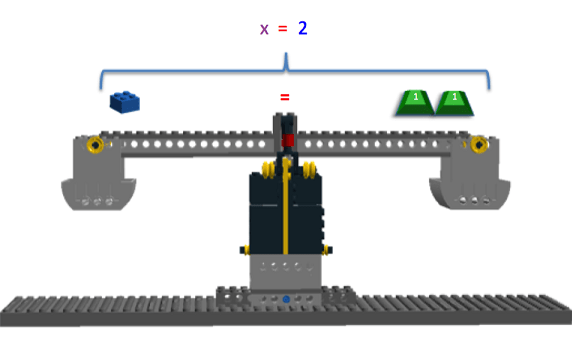

We have found a solution: x = 2! Once a solution is found, it must be checked to make sure it is correct. To check the answer, use the original equation, 3x – 2 = 4, and plug in the value of 2 for x. Figure 15 shows x replaced with the value of 2.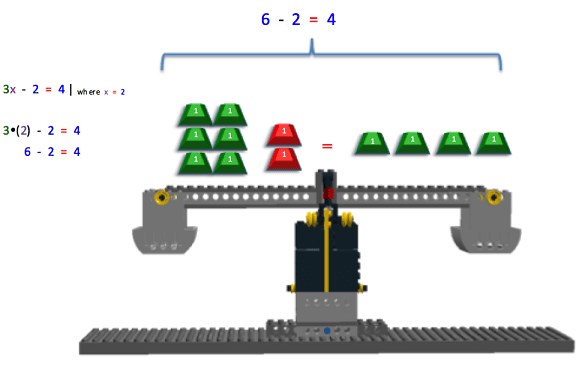

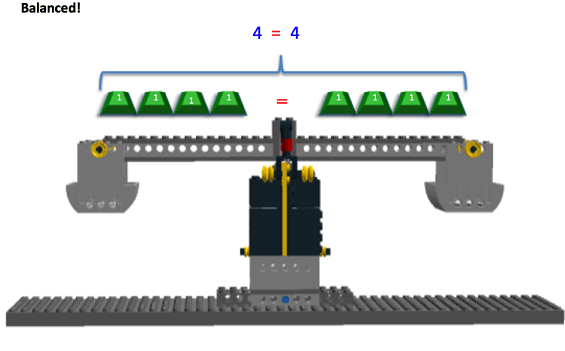
Before the Activity

1. Assemble one LEGO Balance Scale per group using available LEGO parts, LEGO EV3 MINDSTORMS brick and one color sensor. The LEGO instructional building guide for the LEGO Balance Scale is available at https://www.teachengineering.org/lego/building_instructions_balancing/building_instructions_balancing.html. The last page of the instructional building guide provides a full list of all the LEGO pieces used for building the LEGO Balance Scale. If necessary, it is okay to make part substitutions for LEGO bricks and pieces that you might not have. However, be aware of vital parts that are imperative to the make the LEGO Balance's seesaw mechanism work (such as the part labeled as the technic brick).
2. Connect a cable to the color sensor and port 1 of the LEGO EV3 Brick.
3. Program the LEGO EV3 Brick using the provided Balancing Act Program.

• You must install the LEGO MINDSTORMS EV3 software FIRST in order to program the brick with the Balance Act Program.
• Instructions (under Help -> Help and Support menu) are available in the LEGO EV3 MINDSTORMS software to assist you with getting started with EV3 programming, downloading the program to the brick and running the program.
• Other extremely useful tips and troubleshooting support is given as well (for example, information about cables, port and EV3 buttons). Be sure to take a look!

4. If necessary, review concepts of algebra, solving for unknown variables and the idea of balancing equations prior to starting the activity with students.
5. Before the start of the activity, give students the Balancing Equations Pre-Assessment.
6. One-step and two-step equations are provided in the Balancing Equations Activity Worksheet as examples to be completed during the activity; however additional examples can be made up. Keep in mind that examples and answers must be feasible using the masses that are available in the mass kit being used.

   

With the Students

This activity can be separated into two methods of interaction with the LEGO Balance Scale.

• Option 1: First on paper and by hand, students are given an equation from the Balancing Equations Activity Worksheet to solve for the unknown variable. To verify their solution for the unknown variable, students use the LEGO Balance Scale.
• Option 2: Students are given an equation to initially configure on the LEGO Balance Scale. Students use the LEGO Balance Scale to solve for the unknown variable by moving pieces from the left and right sides of the balance scale. Students' solution is correct if their result is balanced.

Option 1 – Use the LEGO Balance Scale to verify the solution:

1. Turn on the LEGO MINDSTORMS EV3 Intelligent Brick by pressing the orange rectangular button.
2. Select the Balancing Act Program to run. Run the program

• A :-) icon appears on the LEGO MINDSTORMS EV3 Intelligent Brick screen signifying the LEGO Balance Scale is balanced and ready to use.
• If a :-( icon initially appears, then the LEGO Balance Scale must be calibrated to balance. Try adjusting the Balance Indicator in front of the color sensor to be sure that the yellow flat LEGO piece is directly in front of the color sensor. Additionally if necessary, use small LEGO pieces to calibrate the leveling of the LEGO Balance Scale by adding pieces to either the right or left side of the scale. Once balanced, a :-) icon appears and the LEGO Balance Scale is balanced and ready to use.

3. Give students an equation to solve for the unknown variable by hand and on paper.
4. To verify their result for the unknown variable, allow students to configure the original given equation on the LEGO Balance Scale using designated pieces to represent terms in the original equation (a LEGO brick for the unknown variable, LEGO plates for the unknown variable's coefficient, and green or red gram masses for positive or negative constants).

• Note: The LEGO Balance scale initially will be unbalanced until the unknown variable's LEGO brick is replaced with a corresponding gram mass.
• An example of how to configure the LEGO Balance Scale with designated pieces is provided in the Background section.

5. Students should substitute the LEGO brick that is configured on the LEGO Balance Scale representing an unknown variable with the solved value using a corresponding number of gram masses.

• Example: If the solved variable x = 5, then replace the LEGO brick with a 5 gram mass.

6. After the unknown variable has been substituted for its corresponding mass on the LEGO Balance Scale, the EV3 Intelligent Brick determines whether or not the result is correct and balanced.

• The LEGO Balance Scale initially begins to waver up and down to stabilize weight added to the scale.
• Once the LEGO Balance Scale is stabilized, the brick displays a :-) icon on screen if the LEGO Balance Scale is correctly balanced. Otherwise the brick displays a :-( icon on screen if the LEGO Balance scaled is not correctly balanced.

7. If the result is correct, congratulate students on a job well done! If a result is incorrect, encourage students to go back and try the problem again until their results end with a :-).

Option 2 – Use LEGO Balance Scale to Solve and Verify Solution:

1. Turn on the brick by pressing the orange rectangular button.
2. Select the Balancing Act Program to run. Run the program.

• A :-) icon appears on the brick screen signifying the LEGO Balance Scale is balanced and ready to use.
• If a :-( icon initially appears, then the LEGO Balance Scale must be calibrated to balance. Try adjusting the Balance Indicator in front of the color sensor to be sure that the yellow flat LEGO piece is directly in front of the color sensor. Additionally if necessary, use small LEGO pieces to calibrate the leveling of the LEGO Balance Scale by adding pieces to either the right or left side of the scale. Once balanced, a :-) icon appears and the LEGO Balance Scale is balanced and ready to use

3. Give students an equation to solve for the unknown variable using the LEGO Balance Scale.
4. Allow students to configure the given equation on the LEGO Balance Scale using a LEGO brick for the unknown variable, LEGO plates for the unknown variable's coefficient, and green or red gram masses for positive or negative constants, respectively.

• Note: The LEGO Balance scale will initially be unbalanced until the unknown variable's LEGO brick is replaced with a corresponding gram mass.
• An example of how to configure the LEGO Balance Scale with designated pieces is provided in the Background section.

5. Using the LEGO Balance Scale, allow students to directly solve for the unknown variable using algebraic and balancing equation manipulation techniques that they have already learned in class. Allow students to note their solutions on paper for the unknown variable.

• An example of how to solve equations using the LEGO Balance Scale is provided in the Background section.

6. To verify a value for the unknown variable, allow students to reconfigure the original equation on the LEGO Balance Scale using a LEGO brick for the unknown variable, LEGO plates for the unknown variable's coefficient, and green or red gram masses for positive or negative constants, respectively.
7. Students should substitute the brick with corresponding gram masses equal to the solved value they've found.

• Example: If the solved variable x = 3, then replace the brick with three 1 gram mass.

8. After the unknown variable has been substituted for its corresponding mass on the LEGO Balance Scale, the brick determines whether or not the result is correct and balanced.

• The LEGO Balance Scale initially begins to waver up and down to stabilize weight added to the scale.
• Once the LEGO Balance Scale is stabilized, the brick displays a :-) icon on screen if the LEGO Balance Scale is correctly balanced. Otherwise the brick displays a :-( icon on screen if the LEGO Balance scaled is not correctly balanced.

9. If the result is correct, congratulate students on a job well done! If a result is incorrect, encourage students to go back and try the problem again until their results end with a :-).

Vocabulary/Definitions

balanced equation: An equation that has equal values on both side of the equal sign.

coefficient: A constant numerical quantity placed before (multiplied by) the unknown variable in an algebraic equation or expression.

color sensor: A sensor that can distinguish between different shadings of light and dark. A color sensor is typically used on robots to help them "see" and detect objects of different light and dark contrast.

constant: A value that does not change.

equation: A mathematical statement that shows that two quantities are equal.

inverse operation: A mathematical operation that is opposite of the mathematical operation being observed.

LEGO MINDSTORMS: A robotics kit made by the LEGO Corporation that contains software and hardware to create small, programmable and customizable robots. Kits include a programmable "brick" computer that controls the system, LEGO parts and a set of modular sensors and motors to create mechanical systems.

one-step equation: An equation that can be solved in one step.

two-step equation: An equation that can be solved in two steps.

variable: A letter or symbol representing an unknown value. This is the quantity that is being solved for in an algebraic equation.

Assessment

Pre-Activity Assessment

The Balancing Equations Pre-Assessment provides generic questions regarding the main principles, usage and solving of equations in order to determine where students' mishaps may fall and where to focus the activity.

Activity Embedded Assessment

The Balancing Equations Activity Worksheet provides comprehensive questions during the completion of this activity to provoke students' critical thinking in a sequential manner.

Post-Activity Assessment

The Balancing Equations Post-Assessment provides comprehensive questions after the completion of this activity to determine students' improvements and opinion based on solving equations.

Safety Issues

• This activity is not suitable for small children based on the small LEGO pieces, which can be a choking hazard.

Troubleshooting Tips

Make sure the yellow brick of the Balance Indicator is configured directly in front of the color sensor in order for the color sensor to detect light to represent a balanced LEGO Balance Scale.

Make sure the LEGO Balance Scale is leveled and balanced prior to solving equations. It may be necessary to calibrate the scale's sides by adding small LEGO pieces to distribute the weight correctly.

Make sure equivalent parts are used on both sides of the LEGO Balance Scale to ensure balance.

The LEGO MINDSTORMS EV3 software has helpful tips and support on getting started with EV3 programming and more under its Help menu.

It can be tricky to solve problems with both positive and negative constants. We recommend differentiating positive constants and negative constants by assigning the gram masses (or the pennies) with a color. For example, a red-marked penny would represent a positive constant, while a blue-marked penny would represent a negative constant. 

Additional Multimedia Support

For information on downloading and installing LEGO MINDSTORMS EV3 Software, please go to: http://mindstorms.lego.com/en-US/News/ReadMore/Default.aspx?id=351333.

References

Copyright

Contributors

Supporting Program

Acknowledgements

This activity was developed under the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.