Visualize Multi-Step Equations: Solving with Seesaws

Accurate step-by-step visualization of a design or plan is crucial for all scientists and engineers when conducting scientific inquiries, research experiments, and most of all, design assessment. The fundamentals of building design require a balance of force, or weight, in all parts of the design, much like a seesaw. A typical seesaw is a structure that handles the weight of multiple people, and can be considered still and balanced if equal weight is placed on both ends, and/or if the weight is distributed equitably along the seesaw beam.

In the world of structural engineering, beams inside buildings are assessed in a similar manner. Weight, or forces, acting on beams must balance in order for the beam and the building itself to stay still and rigid. Small-scale structures and systems are used to test calculations before full-sized structures and systems are constructed, particularly when dealing with designs that millions of people depend on for everyday use, such as a bridge, house or skyscraper. In fact, civil engineers sometimes use seesaw-sized models to test models for force balance and structural stability. Active tinkering, especially when operating a structure or a system, allows for a successful engineering design and helps engineers visualize and assess designs during service use.

After this activity, students should be able to:

• Demonstrate how to solve two-step equations.
• Identify terms in the mathematical equation.
• Explain the use of sensors in a system, especially in feedback control.
• Explain the importance of solving equations in basic structural design.

A basic understanding of solving equations with one unknown.

Two-step equations may not look pleasant on paper. However, learning how to solve them is important for solving many real-world problems that come up in math and science. Two-step equations even come up in daily life. Figuring out how many boxes of cereal you can get with $15 while taking into account coupons or discounts is one example. Calculating if a cardboard box with a weight limit can hold smaller boxes of cans along with other loose cans is another example. The list goes on and on.

A simple example of a two-step equation is shown in Figure 1. Such an equation is composed of variable and constant terms, which can appear on either side of the equation. (Write on the board the Figure 1 equation, along with its corresponding terminology. Solve step-by-step, and you ultimately obtain n = 12.) Solving an equation like this involves moving terms from one side to another, keeping the equation "balanced."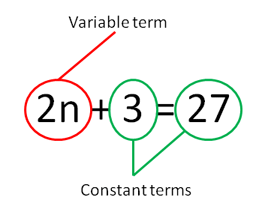Figure 1. Example of a simple two-step equation.CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYU

A good physical example of the use of two-step equations is the seesaw or a physical balance. It is a simple machine made up of a lever that embodies an equation. (Draw a diagram of a seesaw under the equation, positioning the fulcrum under the equal sign). We do not have an equation if there is no balance. In this way, it helps to physically view what you need to do to solve an equation. For example, the Figure 1 equation can be used as follows: you have 27 loose bottles of water on one side of a seesaw, and 3 loose bottles on the other, which are placed alongside 2 full bags of bottles.

Engineers use equations all the time when designing structures or machines. For example, you may have seen a construction site where workers, architects and engineers work together to build the large skyscrapers found in big cities.CopyrightCopyright 2004 Microsoft Corporation, One Microsoft Way, Redmond, WA 98052-6399 USA. All rights reserved.

Most skyscrapers are made of basic structures called beams. Beams are simple structures whose lengths are much longer than their widths and heights. These structures are used in buildings because they are shaped to be stiff enough to resist a lot of bending. They are made of wood, metal or a mix of materials. Many beams are placed inside buildings so that they work together to keep a building standing still.CopyrightCopyright 2004 Microsoft Corporation, One Microsoft Way, Redmond, WA 98052-6399 USA. All rights reserved.

Civil engineers are the type of engineers who design bridges, road, buildings and other structures for our daily use. Believe it or not, the designs behind buildings involve equations, especially when balancing the weight of the entire building. If not balance, a building may tilt or not be able to withstand the amount of weight (load) it was designed to hold. That is why civil engineers check and re-check their work to make sure the design functions, especially for everyone's safety. Engineers go as far as to re-check every single beam in the entire building design to ensure that it remains "balanced" when supporting weight. Keeping that in mind, let's try another example (see Beam Example (PDF)).

With the equipment we have today, we're going to use the help of sensors, which are electronic devices that measure the changes in a system as it is being used. Sensors can be used to measure temperature, distances, the level of light and darkness in a room, weight and other data. Sensors have been used inside buildings and machines to make sure that they are maintained and working correctly. In our activity today, we will use this balance system to help us see if the equations we solve by hand (and by using the seesaw) are "balanced."

Before the Activity

• Gather materials and make copies of the pre-assessment, worksheet and post-assessment handouts.
• Assemble the seesaw, as shown in Figures 2-4. The design of the seesaw can vary; what is provided in this activity is simply a suggested design. The most important thing is for the beam to be balanced. A bungee cord wrapped around the bottom of the 6 ft. beam assists in correctly balancing the beam after each use. Attach the hooks of the bungee cord to the metal rod on each side, and then wrap it around the legs.Figiure 1. How to attach the sensor system to the seesaw beam.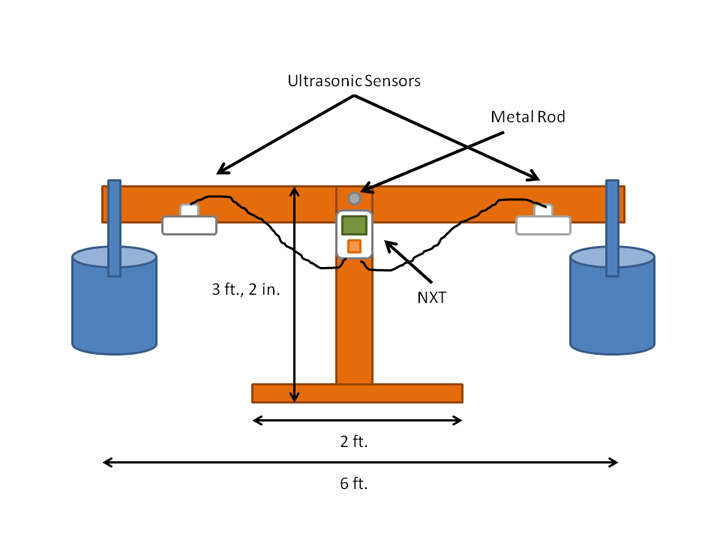CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYUFigure 2. The seesaw activity set-up. Seesaws embody mathematical equations when balanced.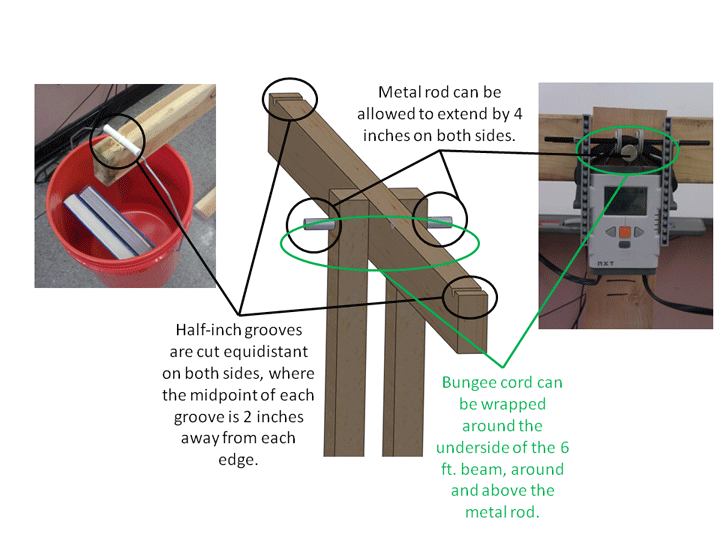CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYUFigure 3. Seesaw construction on top beam.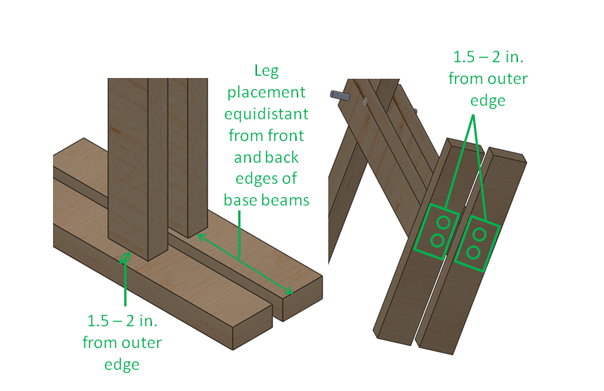CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYUFigure 4. Seesaw construction on bottom base.CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYU
• Attach two ultrasonic sensors to ports 1 and 4 of the LEGO NXT unit.
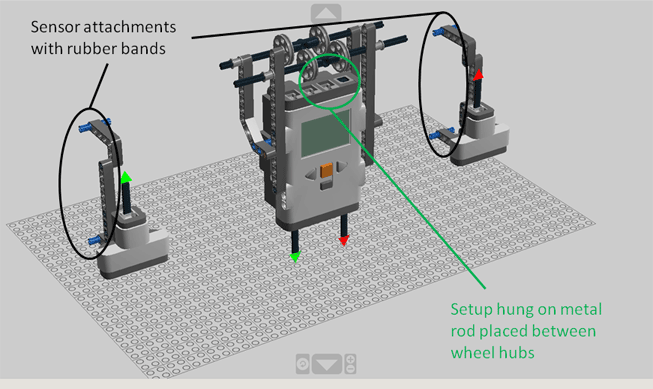
• Construct the set-up shown in Figure 5 using the provided building instructions. Once complete, attach the set-up onto the seesaw, keeping both sensors equidistant from the seesaw fulcrum (legs). Use rubber bands and the pegs in the back of each sensor structure to securely attach them around the 6 ft. beam.Figure 5. LEGO Digital Designer drawing of the LEGO NXT unit and sensors.CopyrightCopyright 2011 Ronald Poveda. Polytechnic Institute of NYU
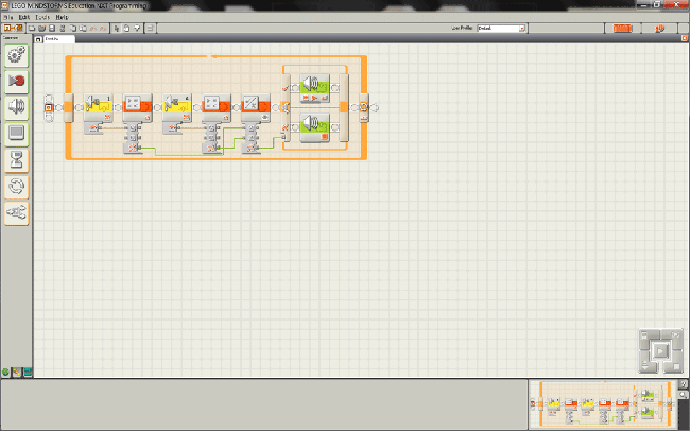
• Create the NXT program that incorporates the two sensors, so that both sensors are incorporated and programmed with respect to a reference distance. Figures 6-7 denote the general program structure.Figure 6. The NXT-G program for the seesaw, with two ultrasonic sensors attached to ports 1 and 4.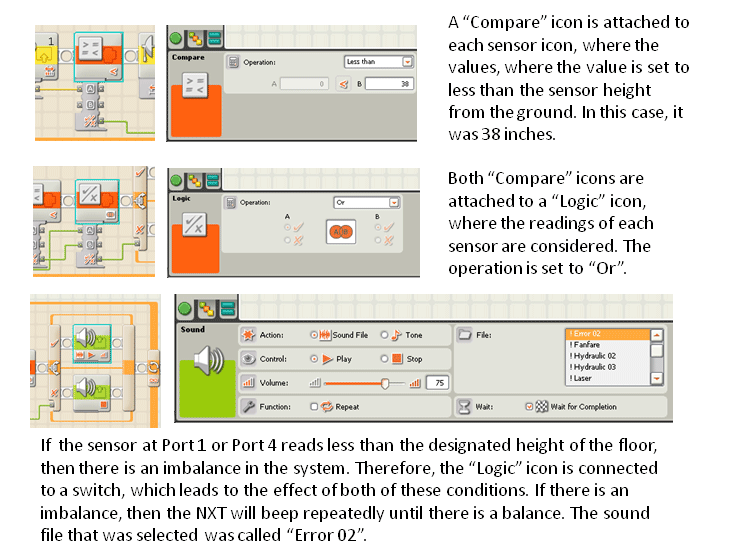CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYUFigure 7. NXT-G program icons used for the seesaw.CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYU
• Position the seesaw near a whiteboard for student use. Place buckets on both sides of the seesaw.
• Using objects of equal weight and size, start placing the appropriate amount of objects on the seesaw. For example, in the equation 3n + 5 = 20, you would know in advance that n = 5. So place 5 water bottles inside 3 closed, opaque bags, since the coefficient in front of the variable "n" is 3. Along with 5 loose water bottles, place the bags with the bottles inside on the left bucket of the seesaw, since "3n + 5" is on the left side of the equation. On the right side of the equation is a 20. So place 20 loose bottles on the right bucket of the seesaw.
• Depending on how many equations assigned for students to work out, take sufficient objects and bags and arrange them for each equation. Place the objects in bags in advance so that it is easy to transition from equation to equation during the activity. Ensure that the bags are closed and fully opaque so that students cannot see inside each bag. For each equation, ensure that the amounts of objects in each bag are equal.

With the Students

1. Direct students to keep the concept of weight balance in mind, where an equal amount of weight is placed on both sides of a fulcrum in order for balance to be achieved. Initially, have them assume that the weight is placed equidistant from the middle of the seesaw. Have them imagine that the top beam of the seesaw is a part of a building, and that their objective is to "balance the beam" using mathematics, particularly the method of two-step equations. Work out the problem in Beam Example (PDF) so that the students can see how math is incorporated in the design of real-world structures.
2. Hand out to each student a Seesaw Worksheet (PDF) of equations to work on for 15 minutes. Have them form groups of 4-5 students each and work on the entire sheet.
3. Assign one question from the worksheet to each group to carry out using the seesaw and the whiteboard.
4. Give each group time to solve their assigned problem step-by-step using the classroom whiteboard and seesaw at the same time. For example, to solve for n in the equation 3n + 5 = 20, we subtract 5 from both sides. So, the group is also expected to remove 5 water bottles from each bucket. To finally solve for n, each side is divided by 3. In a similar fashion, the load in each bucket must be divided by 3. So, one bag is left on one side, while a certain amount of water bottles are left on the other side. In this way, students solve for the amount of water bottles in each bag, and students open the bags to verify.
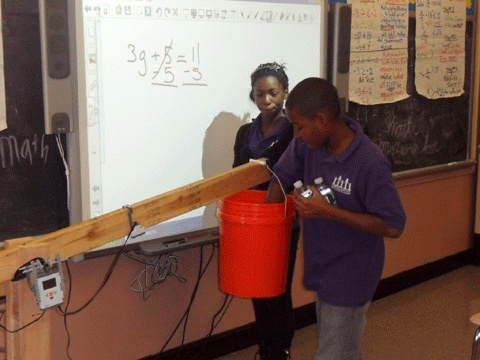
5. If a group incorrectly solves the equation, the beam should be unbalanced, and the class should hear the NXT beep. If this occurs, warn them that the beam is unbalanced, and that the building is tilting too much. Have them re-check their calculations to correct the imbalance.Students solve an equation using the seesaw set-up.CopyrightCopyright 2011 Ronald Poveda, Polytechnic Institute of NYU

Pre-Activity Assessment

Two-Step Equations: Have students complete the Seesaw Pre-Assessment (PDF) to assess their prior knowledge of solving two-step equations.

Real-World Conceptual Identification: Before the activity, briefly identify and discuss two-step equations, as well as some real-world examples. Ask students how two-step equations are involved in the design of buildings and large-scale structures. Does the design of bridges and skyscrapers involve solving equations? (Answers: Yes! The design of bridges and skycrapers involve solving equations based on forces, moments, length and width dimensions, area, volume and many other concepts. In the process of planning these structures, engineers solve many equations to make sure everything will fit together correctly and the structure will support itself and not fall down. These equations involve two-step equations and some equations that take even more than two steps to solve!) Make sure that students realize that structures and buildings, much like equations, need to be balanced in terms of weight.

Activity Embedded Assessment

Analogies and Real-World Examples: Evaluate students on the following criteria: cooperation in problem solving, and step-by-step reasoning using a physical analogy of the problem at hand. Since they are working in groups, all students in the group must participate and cooperate with each other. It is also important for each group to demonstrate a logical progression from each step to the next in order to understand how to solve basic two-step equations. Ask students: What other kinds of existing structures require such mathematical analysis? (Possible answers: Factory machinery, or objects in their own homes.) For example: What needs to be considered to build a kitchen table? What objects and forces does a kitchen table need to support? (Possible answers: The weight of plates and bowls of food, bags of groceries, a vase of flowers, a person leaning on it.) Ask: Does the structure or object need to be balanced? Can you help make sure it is balanced using mathematical equations? (Answer: Yes, by using mathematical equations, you can determine how much force from the load on the table is distributed to each leg or support of the table. If you were designing the table, you could test the material you wanted to use to make sure the legs or supports of the table could hold the weight of a Thanksgiving dinner or a seven-layer wedding cake, for example.)

Post-Activity Assessment

Class Discussion: Re-iterate the importance of mathematics in building design. To give a general idea of the amount of work engineers undergo to assess building designs, ask students how many equations engineers may have to solve when dealing with the design of a skyscraper. Are beams the only structures inside of buildings that can be designed using equations? (Answer: No, many other objects within a structure can be designed using equations. A table is a one example that we already mentioned. We focused on beams because they play a major supporting role in large structures. Many equations must be solved to make sure each beam can support the load expected to be applied to it. Larger structures usually means more beams... and more equations to solve!) As an additional inquiry, ask students: How might how sensors play roles in building design and assessment? Do you think that buildings can use sensors? How and why? (Answer: Sensors can be used to measure the force being applied to a particular beam based on its load. Also, as in our activity today, sensors can be used to collect all sorts of data, such as to make sure things are level. That's important for how things look, but even more important for building stability. If a force causes a beam to lean or fall in one direction, a sensor can alert an engineer that this is happening before the beam leans or falls so far that other objects it is supporting fall down as well.)

Test: Have students complete the Seesaw Post-Assessment (PDF) to demonstrate their understanding of solving two-step equations.

• Have an adult standing nearby to control the motion of the seesaw as students transfer weight from one bucket to another. It also helps if team members using the seesaw set-up help to stabilize the seesaw's motion and work together.

After each weight transfer, level the seesaw by hand and then let it balance by itself, so that the ultrasonic sensors can read the correct distance from the floor.

Make sure that no nearby objects (such as tables, desks or your own arms, legs and feet) are too close to the sensors, since they may obstruct the sensor's readings.

Create a force balance activity using a similar structure. Using the concepts of force and moment, cut several notches into the beam so that the distance from the seesaw center to each load on the beam becomes another parameter to consider for beam balance.