Quick Look
Summary
Students use a hurricane tracking map to measure the distance from a specific latitude and longitude location of the eye of a hurricane to a city. Then they use the map's scale factor to convert the distance to miles. They also apply the distance formula by creating an x-y coordinate plane on the map. Students are challenged to analyze what data might be used by computer science engineers to write code that generates hurricane tracking models. Then students analyze a MATLAB® computer code that uses the distance formula repetitively to generate a table of data that tracks a hurricane at specific time intervals. Students come to realize that using a computer program to generate the calculations (instead of by hand) is very advantageous for a dynamic situation like tracking storm movements. Their inspection of some MATLAB code helps them understand how it communicates what to do using mathematical formulas, logical instructions and repeated tasks. They also conclude that the example program is too simplistic to really be a useful tool; useful computer model tools must necessarily be much more complex.Engineering Connection
High school students are familiar with computer science primarily as proficient users of video games and cell phone apps and may have little idea of the programming they require. Through this activity, students are exposed to a simple computer code as a real-world application of conditional statements and the distance formula with the potential to help save lives. Students become familiar with the steps of the engineering design process as they figure out by their own methods how far the storm is and how quickly it will make landfall. They also analyze computer code, use it to obtain data, determine incorrect model assumptions and suggest ways to improve the simulator.
Computer science is a branch of engineering that focuses on writing software to solve problems. Deductive reasoning and if-then conditional statements are at the core of computer science programming. Engineering researchers use software like MATLAB to write code to solve complex mathematical problems and run simulations. Sometimes these simulations generate visual representations of the research results, helping researchers explore new setups or algorithms at low cost.
Learning Objectives
After this activity, students should be able to:
- Develop and apply the distance formula and an x-y coordinate plane on a hurricane tracking map.
- Use a map scale to determine distance in miles.
- Explain the use of if-then logical reasoning statements in computer code.
- Use MATLAB computer science programming language to help understand and solve critical problems that are important to our society.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-1. Analyze a major global challenge to specify qualitative and quantitative criteria and constraints for solutions that account for societal needs and wants. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Analyze complex real-world problems by specifying criteria and constraints for successful solutions. Alignment agreement: | Criteria and constraints also include satisfying any requirements set by society, such as taking issues of risk mitigation into account, and they should be quantified to the extent possible and stated in such a way that one can tell if a given design meets them. Alignment agreement: Humanity faces major global challenges today, such as the need for supplies of clean water and food or for energy sources that minimize pollution, which can be addressed through engineering. These global challenges also may have manifestations in local communities.Alignment agreement: | New technologies can have deep impacts on society and the environment, including some that were not anticipated. Analysis of costs and benefits is a critical aspect of decisions about technology. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-4. Use a computer simulation to model the impact of proposed solutions to a complex real-world problem with numerous criteria and constraints on interactions within and between systems relevant to the problem. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use mathematical models and/or computer simulations to predict the effects of a design solution on systems and/or the interactions between systems. Alignment agreement: | Both physical models and computers can be used in various ways to aid in the engineering design process. Computers are useful for a variety of purposes, such as running simulations to test different ways of solving a problem or to see which one is most efficient or economical; and in making a persuasive presentation to a client about how a given design will meet his or her needs. Alignment agreement: | Models (e.g., physical, mathematical, computer models) can be used to simulate systems and interactions—including energy, matter, and information flows—within and between systems at different scales. Alignment agreement: |
Common Core State Standards - Math
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Apply geometric methods to solve design problems (e.g., designing an object or structure to satisfy physical constraints or minimize cost; working with typographic grid systems based on ratios).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Reason quantitatively and use units to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Evaluate reports based on data.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the effects of technology on the environment.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the role of society in the development and use of technology.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop abilities to use and maintain technological products and systems.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop abilities to assess the impact of products and systems.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of engineering design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the attributes of design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Use computers and calculators to access, retrieve, organize, process, maintain, interpret, and evaluate data and information in order to communicate.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Design forecasting techniques to evaluate the results of altering natural systems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Illustrate principles, elements, and factors of design.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Synthesize data and analyze trends to make decisions about technological products, systems, or processes.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use various approaches to communicate processes and procedures for using, maintaining, and assessing technological products and systems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Demonstrate the use of conceptual, graphical, virtual, mathematical, and physical modeling to identify conflicting considerations before the entire system is developed and to aid in design decision making.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Connect technological progress to the advancement of other areas of knowledge and vice versa.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Assess a technology that minimizes resource use and resulting waste to achieve a goal.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Texas - Math
-
select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
solve mathematic and scientific formulas, and other literal equations, for a specified variable.
(Grade
9)
More Details
Do you agree with this alignment?
-
Mathematical modeling in science and engineering. The student applies mathematical processes with algebraic techniques to study patterns and analyze data as it applies to science. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
identify and determine the validity of the converse, inverse, and contrapositive of a conditional statement and recognize the connection between a biconditional statement and a true conditional statement with a true converse;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Coordinate and transformational geometry. The student uses the process skills to understand the connections between algebra and geometry and uses the one- and two-dimensional coordinate systems to verify geometric conjectures. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
use scale factors with two-dimensional and three-dimensional objects to demonstrate proportional and non-proportional changes in surface area and volume as applied to fields;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Two-dimensional and three-dimensional figures. The student uses the process skills in the application of formulas to determine measures of two- and three-dimensional figures. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
derive and use the distance, slope, and midpoint formulas to verify geometric relationships, including congruence of segments and parallelism or perpendicularity of pairs of lines; and
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
For the teacher's introductory presentation:
- computer (with Microsoft Excel® and Internet access) and LCD projector to show the class a satellite image of Hurricane Ike (Figure 1), an example Hurricane Tracking Assignment spreadsheet, an online video and an online animation
- MATLAB software installed on the teacher's computer to run the MATLAB code; obtain a trial version or purchase a license at http://www.mathworks.com/products/matlab/ (strongly recommended, although the activity can be completed without MATLAB by using the data on the Hurricane Tracking Results, a Microsoft Excel® spreadsheet, which was generated using the MATLAB code and software)
- hurricane.m file
- hurricane.dat file
Each group needs:
- computer with Microsoft Excel® and MATLAB
- Hurricane Tracking Map (see Figure 2)
- Hurricane Tracking Assignment, a Microsoft Excel® spreadsheet
- MATLAB Code, in the form of a Microsoft Word® or PDF file for easy printing
- ruler with centimeters marked
- crayons, markers (or dry erase markers if using a laminated map)
- calculator
For the entire class to share:
- (optional) LCD projector, so students can display to the class their data and MATLAB software calculations
Note: As an alternative to the provided Hurricane Tracking Map, which uses a grid measured in miles, find a map that uses kilometers and modify the activity to use the metric system. Or, purchase large NOAA Atlantic hurricane tracking charts, from 18 x 24-inches to 60 x 80-inches, paper or laminated at http://www.swiftmaps.com/servlet/Detail?gclid=CL2TyN32xbgCFatj7AodgAoA5g&no=568.
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/uoh_hurricane_activity1] to print or download.Pre-Req Knowledge
Students are expected to know:
- How to plot points on an x-y coordinate plane.
- A basic understanding of scale factors on maps.
- The distance formula.
- A basic understanding of a hurricane.
Introduction/Motivation
A significant problem for people who live in coastal areas is the threat of major hurricanes. Being able to predict the path of a storm is paramount to save lives and protect property. Today, we will look at a simulation that shows how destructive the sustained winds of a hurricane can be. You will also follow the steps of the engineering design process and use some simple tools to figure out how far the storm is from land and how quickly it will make landfall. You will also brainstorm how computer science engineers might be able to help during such a threat. You will examine a simple, but real computer code that uses the distance formula, which will give you an idea of the complexity of computer programming.
Whether you realize it or not, you are already familiar with computer science because of the technology we use every day—such as video games and cell phone apps. Many of you are quite skilled at video games and better than me at using phone apps. However, do you have any idea of the creative programming required to make them possible?
Procedure
Background
Hurricanes are a yearly threat to U.S. coastal areas. Most coastal cities have developed preparedness plans and encourage residents to be ready to withstand major storm weather and/or evacuate during hurricane season. The hurricane season typically runs from June 1 through November 30. The National Oceanic and Atmospheric Administration (NOAA) makes forecasts.
Once a hurricane is identified and named, the primary concern is predicting its path. Several computer models exist to supply newscasters with predicted paths generated from the simulations. A tropical cyclone or hurricane forecast model is a computer program that uses meteorological data to forecast aspects of the future state of tropical hurricanes.
Two models are typically used by newscasters: The U.S. Model and the European Model. The Weather Channel Website (TWC) contains videos that explain both. When people learn that a model predicts that a hurricane may land on their city, they usually want to know how much time before the hurricane arrives, which depends on the hurricane traveling speed, its size and its distance away.
This activity attempts to create a very simple hurricane model using MATLAB to predict how fast the hurricane will travel. It applies to geometry as it uses deductive reasoning, if-then conditionals and the distance formula. During the activity, students perform hurricane tracking calculations by hand, filling in a paper spreadsheet, and then use MATLAB to generate the (same) results, which they enter into a digital Excel® version of the spreadsheet. The point of the hand calculations is for students to realize the power of using computers to perform the calculations required to track hurricanes.
Also during the activity, students have the opportunity to observe and critique the many limitations of this simple model, which helps them get an idea of how complex the computer code must be for a real model. The concept of similarity and scale factors are also used, and the teacher may want to modify the activity to include similar right triangles and the Pythagorean Theorem.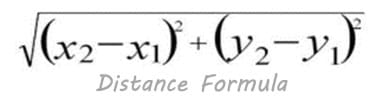
The distance formula is a numerical description of how far apart objects are. More specifically, it is an equation used to find the Euclidean distance between two points on an x-y coordinate plane, where the first point has coordinates (x1, y1) and the second point has coordinates (x2, y2). The distance formula is the square root of (x2-x1) squared plus (y2-y1) squared.
The engineering design process is a series of steps used by engineering teams to guide them as they develop new solutions, products or systems. Typically, the steps include defining a problem, brainstorming, researching and generating ideas, identifying criteria and specifying constraints, exploring possibilities, selecting an approach, developing a design proposal, making a model or prototype, testing and evaluating the design using specifications, refining the design, creating or making it, and communicating processes and results. Throughout this activity, students generally follow this sequence of steps.
Before the Activity
- Gather materials and make paper copies of the Hurricane Tracking Map (see Figure 2), Hurricane Tracking Assignment and MATLAB Code, one each per group.
- Prepare each group's computer with Microsoft Excel®, MATLAB and the Hurricane Tracking Assignment and Hurricane Tracking Assignment with Comments Excel® files.
- Practice using MATLAB with the hurricane.dat and hurricane.m files, following the instructions in the Procedure section. If MATLAB is not available, use the data in the Hurricane Tracking Results instead, which was generated using the MATLAB code and software. Note: The MATLAB code that students use outputs the results provided in the Hurricane Tracking Results Excel® file. These results are the same as what students should come up with by doing calculations by hand in step 11.
- Organize the desks in groups of four students each. At each workstation, place a tracking map, ruler, crayons and calculator.
- (optional) For each group of four students, pre-designate a team leader and a materials manager.
- On the teacher's computer with LCD projector, be ready to show the class the following items, using the website addresses in the Additional Multimedia Support section: 1) the NOAA wind scale simulation, 2) a NASA satellite image of Hurricane Ike in 2008, as provided by Wikipedia, 3) a 31-second DIRECT TV ad, Don't Fall into a Dinner Party, as provided at YouTube.
With the Students
- Read aloud to students the following challenge: The morning news just announced that a hurricane in the Gulf could grow into a mammoth size category 4 hurricane. Can math possibly help you save human lives? Can logical reasoning, knowledge of the distance formula, and technology help you escape the hurricane in time? How?!
- Show the one-minute National Weather Service National Hurricane Center animation of the effect of wind speed on human-made structures (like homes) and trees. Watch the damage increase as the wind speed and storm intensity increase. The animation uses a wind scale with a 1 to 5 rating based on a hurricane's sustained wind speed, showing the range of destruction from category 1 to category 5 storms.
- Show students a satellite image of Hurricane Ike. Who remembers Hurricane Ike in 2008? This storm was rated a category 4, a major hurricane, with maximum winds of 145 mph. Take a look at this satellite image. Do you see the center of the hurricane? And how wide the span of the storm is? (Review some of the other descriptive statistics about this storm to show its intensity and impact on people and property in a wide region.)
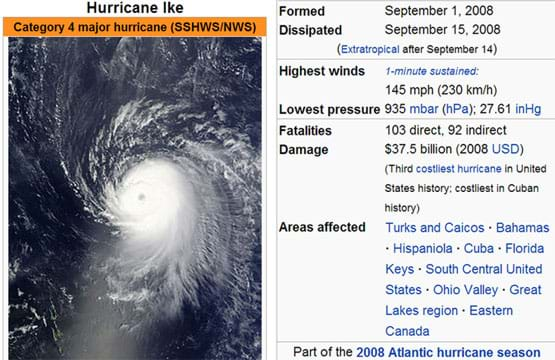
Figure 1. A satellite image of Hurricane Ike at peak intensity in August 2008. - Direct students to conduct the pre-activity assessment—small-group discussion questions—as described in the Assessment section.
- Briefly introduce (or review) the following concepts with the class:
- What is logical or deductive reasoning? Show students the "Don't Fall into a Dinner Party" TV ad as a humorous example of illogical reasoning. The text from the ad: "When you pay too much for cable, you feel powerless. When you feel powerless, you want to take the power back. When you want to take the power back, you take karate. When you take karate, you want to use your karate. When you want to use your karate, you become the Fist of Goodness. When you become the Fist of Goodness, you run along rooftops. And when you run along rooftops, you fall into a dinner party. Don't fall into a dinner party."
- If-then conditional statements
- Computer programming code
- Direct students to conduct a three-minute group discussion of the engineering design process. What are the steps? Are the steps logical? Might we have to repeat steps sometimes? What happens at each step? The design process includes defining a problem, brainstorming, researching and generating ideas, identifying criteria and specifying constraints, exploring possibilities, selecting an approach, developing a design proposal, making a model or prototype, testing and evaluating the design using specifications, refining the design, creating or making it, and communicating processes and results. Tell students that just like engineers, they will be following the steps of the engineering design process during the course of the activity.
- Define the Problem : Give teams time to discuss the three most important questions that need to be answered when people find out that a hurricane is predicted to make landfall on their city.
- How big? What is the predicted category (storm severity, strength, size) of the hurricane when it makes landfall?
- How far away? How far away is the hurricane?
- How soon? How quickly is it expected to make landfall?
- Brainstorm: Direct groups to brainstorm (and record) their ideas to answer these questions:
- How can you answer those three questions and what tools could be used?
- Do you feel people should evacuate the city or not?
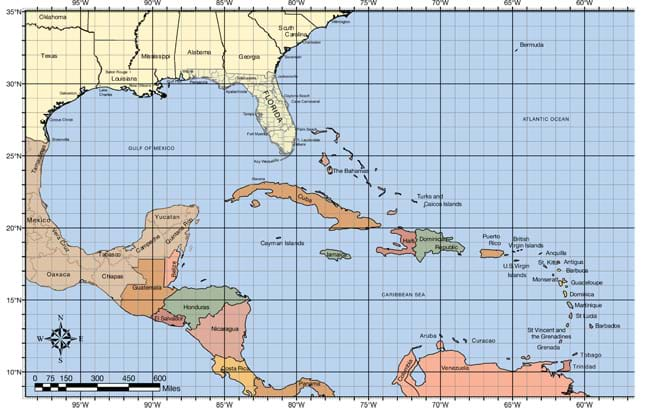
Figure 2. A hurricane tracking map.
- Research and Generate Ideas
- Provide each group with a hurricane tracking map (see Figure 2), a ruler and a calculator. The purpose of a map like this is to help people track a hurricane located somewhere in the Atlantic Ocean or Gulf of Mexico.
- Provide the longitude and latitude coordinates for the current location of the eye of the hurricane (77°W, 18°N). Note: The location is the Jamaica, but do not tell students the country name yet; just give the coordinates.
- Specify that the hurricane is traveling in a straight line at 10 mph (16.09 km/hour).
- With the tools just provided, have groups generate ideas on how to answer the critical questions: How big? How far away? How soon?
- Identify Criteria and Constraints
Ask groups to draw a coordinate plane on the tracking map using a specific city as the origin. The data uses the city of Brownsville, TX.
Outcome: Expect students to figure out that using the map scale can help them estimate the linear distance from the city to the hurricane center. Expect them to be able to make a simple calculation of hours = distance/speed to determine the amount of time to landfall.
- Calculation Procedure
Have groups perform the following process to calculate by hand the (x, y) location at every time interval based on the distance the hurricane has traveled after each time interval. They use their results to populate the Hurricane Tracking Assignment. Outcome: By doing these calculations by hand, students come to realize the value of the computer software to save work and time, since it can do unlimited iterations of the same calculation almost instantaneously by using the distance formula. Students will review this in the upcoming Explore Possibilities section and subsequent steps.
- Based on the longitude and latitude of the hurricane center, have students identify the country nearest to the hurricane.
- Have students determine the scale factor of the map: 1 cm = X miles. (Answer for the provided map: 1 cm = 133 miles.) To convert miles to kilometers, use the conversion factor of 1 mile = 1.60934 km. (Example: 1,507 miles / 1.60934 km per mile = 2,425 kilometers)
- Have students use a ruler to measure the linear distance from the hurricane center to Brownsville, TX. (Note: In this exercise, Jamaica is the location of the eye of the hurricane with longitude 77° west and latitude 18° north. Brownsville, TX, is the city where the hurricane is expected to land with coordinates 97.5° west and 26° north. Expect students to measure ~11.3 cm.)
- Have students convert the linear distance from centimeters to miles using the conversion factor of 1 cm = 133 miles. (Example: 11.3 cm x 133 miles per cm = 1,503 miles.)
- Specify for students the expected traveling speed of the hurricane so they can calculate the time it will take for the hurricane to travel from Jamaica to Brownsville, TX. (It is recommended to assign a different speed to each group.) Emphasize that the activity assumes that the hurricane will travel in a straight line at a constant speed. In this example, the traveling speed used is 10 miles per hour. So expect students to calculate 150.3 hours, which is 6.26 days.
- Have students locate the (x, y) coordinates of the center of the hurricane in miles.
- To accomplish this, measure the side of 1 grid square (on the tracking map) = 0.5 cm. Using the scale factor, this means that every grid square of 0.5 cm = 66.5 miles.
- To create an (x, y) location in miles, draw an x-y coordinate plane using Brownsville, TX, as the origin (0, 0).
- Then count the number of grid squares horizontally to reach Jamaica (20 grids) and multiply this number times 66.5. This is the x-value in miles.
- Next, count the grid squares vertically (-8 grids) to reach Jamaica and multiply times 66.5. This is the y-value resulting in (1330, -532). Note that the y-value is negative because you are counting down from the origin, ending in the fourth quadrant.
- Explore Possibilities
Determining the distance at one location only can be accomplished with the simple tools provided. However, the following is the type of question that engineers are challenged to answer: How could you determine the distance of the hurricane to our city every 24 hours, 12 hours, 5 hours, every hour, at any desired time interval, including time left to landfall?
- Ask students to discuss within their groups what technological advances could help them do the calculations quickly and efficiently.
- Have each group share at least one method that they discussed as a team. Outcome: Expect students to suggest using calculators, cell phone apps or computers as tools.
- Direct students to complete the activity embedded assessment, as described in the Assessment section.
- Select an Approach
- Have students discuss hurricane computer models that they have seen in the news. Ask groups to each determine at least five pieces of information provided by the computer models.
- Also ask the groups to discuss how they think these computer models work and what math and science concepts might be used to create data, images and predicted hurricane paths.
- Ask students to figure out what type of engineers create these computer models.
- Hand out to each group the MATLAB Code.
- Explain how deductive reasoning and if-then conditionals in the form of for-if-end loops are used to write computer programs to generate hurricane tracking models.
- Outcome: Expect students to conclude that attempting to do the calculations by hand or even with handheld calculators is a tedious task. Using a computer program helps generate the calculations instantaneously and allows students/engineers to easily explore the impact of changing variables such as traveling location of the hurricane, traveling speed and time intervals.
- Develop a Design Proposal
- At this point, students begin to use the computers, which have MATLAB installed. They refer to the paper copy of the MATLAB code, which they enter into MATLAB.
- Run MATLAB with the provided MATLAB code and perform the calculations using at least three different sets of data. You may select any location, traveling speed and time interval. Display this on a screen using the projector. Ask each group to select a different speed and time interval.
- Project the MATLAB code and show students the complexity of the code.
- Have students examine the MATLAB code within their groups, looking at the paper copy.
- Give students some time to dissect and discuss the different logical reasoning statements being used in the code, including the for-if-end loop.
- Have students identify the distance formula and other formulas being used in the code. What are these formulas attempting to calculate?
LinearDistance = This is the linear distance calculated using the distance formula after students enter the initial coordinates of the storm (x2, y2) values in miles.
accumtime = The time accumulated based on the time interval selected. For example if the interval is every 10 hours, then accumtime is 10, 20, 30, etc.)
nextlocation = The code calculates the location of the hurricane after every time interval. It simply multiplies interval times speed and subtracts it from the linear distance.
timeland = The code calculates the time remaining before landfall. It simply subtracts the accumulated time interval – total initial time.
for i=1:j This piece of code generates a counter based on j=LinearDistance-(speed*time). It calculates how many times the if-end loop will run. Without the counter, the if-end loop would be infinite.
for-if-end loop = This loop calculates the accumulated time, the next location of the storm after every time interval, and the time before the hurricane lands. It performs the calculations starting at time intervals of one hour to however many hours the user chooses. Using time intervals of one hour generates hundreds of data points.
- Outcome: Students analyze the design of the code and identify its critical parts. Having done this, expect students to realize that writing computer code is very different from writing a description paragraph in an English class or even a mathematical definition. Also expect students to note that the if-end loop is the most critical part of the program since it can generate as many calculations and data points as desired.
- Making a Model or Prototype
If you have access to computers with MATLAB software, follow the steps below. Otherwise, this was already shown to students in step 11 when they performed the calculations by hand.
- Have groups open the Hurricane Tracking Assignment and the Hurricane Tracking Assignment with Comments Excel® files.
- Load the hurricane.m and hurricane.dat files into the MATLAB folder. Have students sit at computers, open MATLAB, and type the word "hurricane" at the prompt.
- Have students enter the (x1, y1) and (x2, y2) locations. Note that the (x1, y1) location is simply (0, 0), unless the teacher changed it.
- The software provides students with the initial linear distance from the hurricane center to the city in miles. If desired, students can convert the distance to kilometers.
- Have students enter a traveling speed for the hurricane. For this activity, use 10 mph (1.609 km/hour).
- Have students enter a time interval. Note that the smaller the time interval, the greater the number of data points generated. Usually a time interval of 10 hours results in 10 to 20 data points. For this activity, use an interval of 10 hours.
- Direct students to open the hurricane.dat file and analyze the graph that pops up. These outputs contain simple formats.
- Direct students to open the hurricane.xls file. (Note: MATLAB creates the hurricane.xls file under the MATLAB directory. Do not move this file from this directory since MATLAB will not modify it unless it is inside the MATLAB directory.) This file has preset headings and number formatting that organizes the data. This file also converts the miles to kilometers.
- Lead a class discussion to review the data contained in these files. Notice that after a certain number of calculations, the numbers start repeating. The only usable data is the data up to the point when the numbers start repeating.
- Once students see the data, have them play around with the software. Make sure they close the hurricane.xls file. It is not necessary to save it, but it must be closed. Students simply need to enter the word "hurricane" at the prompt every time they want to run the simulation, and open the hurricane.dat file or hurricane.xls file to see the results. Have them try different sets of speeds and/or time intervals to see the impact. Outcome: During this exploration time, expect students to try all types of numbers to see how the software responds. This helps them see the impact of the numbers and connects them to the distance formula and computer code.
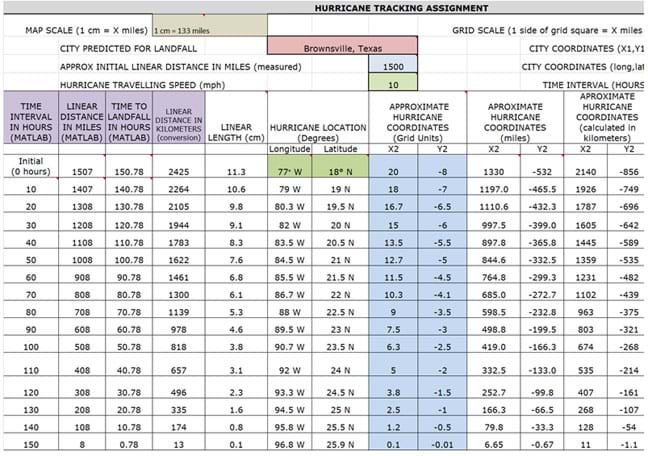
Figure 3. Hurricane tracking assignment answer key. This spreadsheet contains example answers based on a hurricane traveling speed of 10 mph.
- Test and Evaluate the Design
- Direct students to fill out the hurricane tracking assignment Excel® file (aka worksheet).
- Provide students with the longitude and latitude of the location of the hurricane, or use the name of a country as the location. For this activity, Jamaica was used as the starting point and Brownsville, TX, as the city where the hurricane makes landfall.
- Have students test and evaluate the MATLAB computer code by performing the calculations and filling out the required values in the worksheet. If not using MATLAB, use the data in the Hurricane Tracking Results, which was generated using the MATLAB code and software.
- The easiest approach to determine the location of the storm at each interval is to calculate the Linear Length using the Linear Distance in Miles divided by the Map Scale. From this, students can find the longitude and latitude of each location, as well as the (x2, y2) values using the Grid Squares. The hurricane coordinates in miles may be calculated by multiplying the Grid Square values times the grid scale, 1 square = X miles.
- Outcome: Expect completely filled out assignment worksheets from each group.
- Refine/Create or Make the Design
- Ask students: What do you think of the simple computer model you are working with? What do you like about it? What do you not like about it? What could be improved?
- Have teams generate a list of improvements to the computer model. Example improvements:
- The model assumes that the hurricane will travel in a perfectly linear direction, but hurricanes change directions a lot.
- The model assumes that the traveling speed is constant, but hurricanes change their speeds periodically.
- The model does not take into account the radius and diameter of the storm. If the radius of the storm is hundreds of miles in width, it may pose a threat much earlier than the time to landfall.
- The temperature of the water may affect the hurricane path.
- Wind currents may change the hurricane path or speed.
- A high-pressure system may redirect or completely change the hurricane path. Hurricanes travel through the path of least resistance.
- A low-pressure system may increase the traveling speed of the hurricane and help it become larger. The model does not take this into account.
- It would be helpful if the model gave longitude and latitude locations of the center of the hurricane at each time interval.
- It would be helpful if the model provided the (x2, y2) location in miles for each time interval.
- Outcome: Through this brainstorming critique, expect students to quickly see many limitations of the computer model. In fact, this computer model is basically useless if they are really trying to save peoples' lives. However, it does introduce to students the idea of a model and how complex it can be to write computer code that generates useful information.
- Communicate Results
Ask the groups to present their findings. If you use an ELMO or an EIKI projector, have teams display their calculated-by-hand data or the calculations from the MATLAB software.
- Conclusion
Facilitate a class discussion to share and compare results, observations and conclusions. See some suggested questions in the Assessment section. Some concluding points to make:
- The more variables that come into play, the more complex the computer model becomes, and the more complex the mathematical formulas become.
- If all the suggestions for improvement were made, the computer code would be much more complicated, but at the same time how exciting it would be to be able to save lives and protect property by creating an innovative model that is better than any available today. Imagine writing an app for a hurricane tracking model!
- Computer science engineers create simulations of the behavior of hurricanes based on decades of data. This data helps at creating the mathematical formulas or numerical analysis methods necessary to write computer algorithms that can help generate accurate models.
- Today's hurricane computer models are fairly accurate at the state level—they are able to at least predict in which U.S. state a hurricane will land. Considering the necessary complexity of the computer code, that is an admirable accomplishment!
Vocabulary/Definitions
computer model: A simulation to reproduce the behavior of a system.
computer program code: A sequence of instructions written to perform specified tasks with a computer.
computer science: The scientific and practical approach to computation and its applications.
conditional statement: A statement that can be written in the form "if p, then q" where p is the hypothesis and q is the conclusion.
coordinate plane: A plane that is divided into four regions by a horizontal line called the x-axis and a vertical line called the y-axis.
deductive reasoning: The process of using logic to draw conclusions.
distance formula: A numerical description of how far apart objects are. See details in the Procedure > Background section.
engineering design process: A series of steps used by engineering teams to guide them as they develop new solutions, products or systems. See details in the Procedure > Background section.
MATLAB: MATLAB (short for Matrix Laboratory) is a software product by The MathWorks, Inc. that provides a variety of functions and operators for convenient implementation of many numerical methods. The core of MATLAB is the use of matrix computation.
point: The location, or coordinates, of a point are given by an ordered pair (x, y).
scale: The ratio between two corresponding measurements.
Assessment
Pre-Activity Assessment
Discussion Questions: Solicit, integrate and summarize student responses. Within their groups, have students discuss the following questions.
- Have you ever been in a hurricane or know someone who has experienced a hurricane?
- What type of preparations do people make to protect their lives and belongings from hurricanes?
- Have you or someone you know ever evacuated (left their homes and cities) because of an approaching hurricane? How much in advance of the hurricane arrival time did you evacuate?
- What type of information is provided by the news regarding hurricanes?
- What technology, videos, simulations or computer models about hurricanes have you seen on TV? How detailed is the information?
- Have you ever seen or used a hurricane tracking map or hurricane tracking phone app? Was it useful?
- What are the math and science concepts that you believe are used when analyzing the strength, speed and distance to landfall of a hurricane?
Activity Embedded Assessment
Discussion Questions: During the Explore Possibilities step of the Procedures, ask students the following questions:
- What is the most dangerous hurricane category?
- What steps should people take if a category 4 or higher hurricane is predicted to land in their city?
- How is a hurricane tracking map useful for someone who lives in coastal areas that are periodically threatened by hurricanes?
- What are the three main pieces of information people must have if a hurricane is approaching their city?
- What specific tool in a hurricane tracking map helps us find the distance from a hurricane to a city?
- How can technology help to perform complex hurricane-related calculations quickly and efficiently?
Worksheet: During the activity, student groups each complete the Hurricane Tracking Assignment, both a paper copy with hand calculations and a digital copy with MATLAB-generated numbers. For each group, review the accuracy of their worksheets to assess their comprehension of the concepts. Refer to the Hurricane Tracking Assignment Answer Key for example results based on a 10 mph hurricane traveling speed.
Post-Activity Assessment
Discussion Questions: After the activity, ask students to answer the following questions:
- List at least three limitations of the MATLAB hurricane tracking model.
- How difficult it was for you to analyze the MATLAB code? Rate from 1 to 5 with 1 being very easy and 5 being very difficult.
- What was the MATLAB code calculating repetitively (known as iterations)?
- Although the calculations use the distance formula, would you consider this to be a tedious task if you had to do it for 20 time intervals?
- What are five adjectives that you would use to describe computer science engineers?
- If the MATLAB computer model included 51 lines of code and it was very simple, how many lines of code would you estimate a real hurricane tracking computer model might have? Would it be in the tens of thousands, or millions?
- If someone wrote an iPhone app for a hurricane tracking model, and sold it for $1, would you purchase it? Why or why not?
Making Sense: Have students reflect about the science phenomena they explored and/or the science and engineering skills they used by completing the Making Sense Assessment.
Troubleshooting Tips
- Let students perform the activity steps on their own as much as possible. Facilitate as necessary by asking probing questions without providing direct answers.
- MATLAB creates the hurricane.xls file under the MATLAB directory. Do not move this file from this directory since MATLAB will not modify it unless it is inside the MATLAB directory.
- MATLAB may create a hurricane.xlsx (Excel® 2010) file if that is the version you are using. You must close the hurricane.xls file to produce a new one every time you want to change your input information. Otherwise, if the Excel® file is open, MATLAB cannot create a new one with the same name inside the same MATLAB directory.
Activity Extensions
Assign students to watch the news or weather channel, listening and watching carefully about a hurricane being discussed. Then write a paragraph describing in detail what they saw and learned when the newscaster used a computer model. Point out that if they hear the phrase "different computer models show..." it means that a number of computer science engineering teams wrote code in their attempts to generate the best model possible.
Additional Multimedia Support
As part of the activity, show students a one-minute conceptual animation, Hurricane Intensity Scale (Wind Damage), to illustrate the wind damage to trees and homes associated with increasing hurricane intensity; see https://www.nhc.noaa.gov/aboutsshws.php. Or, access the wind damage animation.
As part of the activity, show students a 2008 NASA satellite image of Hurricane Ike, available at Wikipedia at https://en.wikipedia.org/wiki/Hurricane_Ike.
As part of the activity, show students a 31-second DIRECT TV ad, Don't Fall into a Dinner Party, as a funny example of illogical reasoning; see https://www.youtube.com/watch?v=tlUqMmfiaME.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!References
Chang, Justin and K. B. Nakshatrala. Modification to Darcy Model for high-pressure and high-velocity applications and associated mixed finite element formulations, arXiv: 1306.5216v1 [cs.NA], 2013. Cornell University Library. Accessed July 17, 2013. http://arxiv.org/abs/1306.5216
Chapra, Steven C. and Raymond P. Canale. Numerical Methods for Engineers, Sixth edition. New York, NY: McGraw Hill, 2010. http://highered.mheducation.com/sites/0073401064/information_center_view0/index.html
Nakshatrala, K. B. and K. R. Rajagopal. A numerical study of fluids with pressure dependent viscosity flowing through a rigid porous medium. International Journal for Numerical Methods in Fluids, 67:342-368, 2011. Accessed July 17, 2013. http://arxiv.org/abs/0907.5234
Tropical Cyclone Forecast Model. Last updated July 17, 2013. Wikipedia, The Free Encyclopedia. Accessed July 17, 2013. http://en.wikipedia.org/wiki/Tropical_cyclone_forecast_model
Copyright
© 2014 by Regents of the University of Colorado; original © 2013 University of HoustonContributors
Armando Vital, K. B. Nakshatrala, Justin Chang, Fritz Claydon, Rodrigues, Stuart LongSupporting Program
National Science Foundation GK-12 and Research Experience for Teachers (RET) Programs, University of HoustonAcknowledgements
This digital library content was developed by the University of Houston's College of Engineering under National Science Foundation GK-12 grant number DGE 840889. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.
Last modified: October 22, 2020




User Comments & Tips