Quick Look
Grade Level: 11 (9-12)
Time Required: 1 hour
Lesson Dependency:
Subject Areas: Computer Science, Data Analysis and Probability, Physics
NGSS Performance Expectations:

| HS-PS2-1 |

Summary
Students prepare for the associated activity in which they investigate acceleration by collecting acceleration vs. time data using the accelerometer of a sliding Android device. Based on the experimental set-up for the activity, students form hypotheses about the acceleration of the device. Students will investigate how the force on the device changes according to Newton's Second Law. Different types of acceleration, including average, instantaneous and constant acceleration, are introduced. Acceleration and force is described mathematically and in terms of processes and applications.Engineering Connection
In this lesson, students review the topic of acceleration to prepare for an experiment in which they gather acceleration data using a mobile application. In engineering, it is critical to record and analyze data to be able to correctly solve problems. For example, civil engineers use mathematical equations to make predictions, as well as design experiments to measure tolerances and strengths to build bridges and other structures. They mathematically analyze data from their experiments to learn how to fix existing problems and create better structures. Every engineering discipline requires engineering analysis on observed and measured data. This lesson prepares students to use engineering mechanics analysis skills that a mechanical engineer might employ on a daily basis.
Learning Objectives
After this lesson, students should be able to:
- Define acceleration.
- Describe the relationship between position, velocity and acceleration.
- Use equations of motion to solve for unknown variables.
- Use Newton's second law of motion to quantify the force acting on the device at a given location.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-1. Analyze data to support the claim that Newton's second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Analyze data using tools, technologies, and/or models (e.g., computational, mathematical) in order to make valid and reliable scientific claims or determine an optimal design solution. Alignment agreement: Theories and laws provide explanations in science.Alignment agreement: Laws are statements or descriptions of the relationships among observable phenomena.Alignment agreement: | Newton's second law accurately predicts changes in the motion of macroscopic objects. Alignment agreement: Attraction and repulsion between electric charges at the atomic scale explain the structure, properties, and transformations of matter, as well as the contact forces between material objects.Alignment agreement: | Empirical evidence is required to differentiate between cause and correlation and make claims about specific causes and effects. Alignment agreement: |
Common Core State Standards - Math
-
Graph exponential and logarithmic functions, showing intercepts and end behavior, and trigonometric functions, showing period, midline, and amplitude.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Determine the best approach by evaluating the purpose of the design.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Council of Teachers of Mathematics - Math
-
Use mathematical models to represent and understand quantitative relationships
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
Select and use appropriate statistical methods to analyze data
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
Develop and evaluate inferences and predictions that are based on data
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
National Science Education Standards - Science
-
Use technology and mathematics to improve investigations and communications. A variety of technologies, such as hand tools, measuring instruments, and calculators, should be an integral component of scientific investigations. The use of computers for the collection, analysis, and display of data is also a part of this standard. Mathematics plays an essential role in all aspects of an inquiry. For example, measurement is used for posing questions, formulas are used for developing explanations, and charts and graphs are used for communicating results.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Nebraska - Math
-
Make inferences and justify conclusions from sample surveys, experiments, and observational studies.
(Grade
12)
More Details
Do you agree with this alignment?
Nebraska - Science
-
Recognize creativity, imagination, and a good knowledge base are all needed to advance the work of science and engineering
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/uno_accelerometer_lesson02] to print or download.Pre-Req Knowledge
A basic understanding of the Android device and how to install and run the provided Android application. Students should also be familiar with derivatives and integrals, as well as be comfortable graphing and completing calculations with the sine function.
Introduction/Motivation
Today, we will review the topic of acceleration to get prepared for our upcoming activity, as well as make predictions on what will happen in the activity. You will observe an object speeding up and slowing down, and discuss the motion of the object. Newton's second law of motion describes how acceleration and mass can determine the force acting on that object. The object will be an Android device, either a cell phone or tablet (Refer to the Exploring Acceleration with an Android activity for more details). This will be demonstrated using the following set-up (draw Figure 1 on the classroom board).

During the activity, as I stretch the rubber band, you will observe the Android device while it is accelerated across the two rows of text books. You will make observations and discuss the device's motion, as well as analyze the data collected by the Android device. To prepare for this activity, we will start by forming hypotheses about the device's acceleration. Let's start by making some predictions based on this set-up. (Ask students the following questions to start a class discussion focused on generating hypotheses for the upcoming activity. Example answers are provided.)
- What will be the motion of the device? Describe this motion you expect to happen. (Answer: The device should speed up when it is first released and then slow down until it comes to a stop.)
- Will the acceleration of the device be constant? What about the force acting on the device? (Answer: The acceleration will not be constant since the device will speed up then slow down. Since the rubber band will not maintain the same "stretch," the force on the object will not be constant and since the mass of the object stays the same then according to Newton's second law of motion the acceleration must change. This means that the acceleration will change over time.)
- Will the velocity of the device ever be negative? (Answer: The device will travel in one direction only, so the velocity will always be either positive or always negative depending on which direction we call positive. However integration could result in negative velocity when only positive velocity is expected. Students need to be aware of this.)
- Will the acceleration of the device ever be negative? (Answer: Yes. Since the device will both speed up and slow down, it will have both positive and negative acceleration, no matter how we orient the directions.)
- What would an acceleration vs. time graph look like for this demonstration? (Answer: The graph should resemble one period of a sinusoidal graph, with a maximum followed by a minimum (see Figure 2) or the graph will appear similar to the function, f(x)=(-bx)/(x2+1), translated to the right where b is a scale factor. Note: Figure 2 uses data collected from the experiment.)
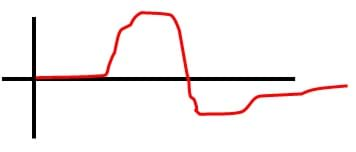
Figure 2. A graph of experiment data collected by a student group.
Lesson Background and Concepts for Teachers
Acceleration
Putting Acceleration in Recognizable Terms: In common words, acceleration is used to measure a change in speed of an object, either increasing (acceleration) or decreasing (deceleration). This definition is not completely accurate because it disregards the direction component of the velocity vector.
Putting Acceleration in Conceptual Terms: Acceleration is a quantity in physics defined as the rate of change in the velocity of an object over time. Since velocity is a vector, acceleration describes the rate of change in the magnitude and direction of the velocity of an object. When thinking in only one dimension, acceleration is the rate that an object speeds up or slows down.
Putting Acceleration in Mathematical Terms: Many different mathematical variations for acceleration exist. Below is a partial listing:
- Newton's second law of motion: For a body with constant mass, the acceleration is proportional to the net force acting on it. Fnet = ma
- Rate of change in velocity with respect to time, slope of velocity vs. time graph (two forms):

- Instantaneous acceleration is the second derivative of a position function for an object in motion. The first derivative is the instantaneous velocity and the second derivative is instantaneous acceleration.
- Constant Acceleration is where the velocity of an object in motion changes by an equal amount in equal interval time periods. Using algebra the following kinematic equations can be derived.
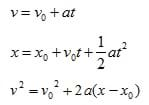
- Putting Acceleration in Process terms: To compute the acceleration of an object, it is essential to first understand the type of motion occurring. Once the type of motion is determined, a variety of mathematical equations can be used, depending on the situation. Unfortunately, the acceleration is only easy to find in situations in which the object's motion is predictable.
- Putting Acceleration in Applicable terms: Any real-life application in which an object is in motion provides an example in which the object has some acceleration. If the object's velocity is changing, the object is accelerating or decelerating. If the object has constant velocity, the acceleration of the object is zero. If an object is moving at a constant speed following a circular path, the object is experiencing a constant acceleration in the direction that points toward the center of the circle.
- Graphical Relationships: It is important to remember the relationship between velocity and acceleration when studying a velocity vs. time graph or an acceleration vs. time graph. Remember that acceleration is the rate of change of velocity. Given a velocity vs. time graph, acceleration can be calculated by finding the rate of change, or slope, of the graph, as this is the rate of change of velocity with respect to time. Given an acceleration vs. time graph, the area under curve gives the change in velocity of an object from the object's initial velocity. If the object starts at rest, the area under the acceleration vs. time curve gives the actual velocity of the object at a given time. If the object travels only in one direction, velocity and speed are equal. The maximum velocity of the object occurs when the acceleration changes from positive to negative. The actual maximum velocity can be approximated by first approximating the time value of any change in sign (+ to – or – to +) of the acceleration and then integrating the acceleration vs. time curve from zero to that time value.
Associated Activities
- Exploring Acceleration with an Android - Students investigate acceleration by collecting acceleration vs. time data using the accelerometer of a sliding mobile Android device. They use a mobile app for the Android device to collect and analyze data related to its horizontal acceleration (along the "x-axis"). Using the data, they create velocity vs. time graphs and approximate the maximum velocity of the device.
Vocabulary/Definitions
acceleration: The rate that an object's velocity changes with time.
average acceleration: The average acceleration of an object over a period of time, found by taking the change in velocity of the object during that period of time and dividing by the length of time.
constant acceleration: The constant or equal change in velocity of an object in uniform lengths of time.
derivative: A measure of how a function changes as its input changes.
function: A relation between a set of inputs and a set of allowable outputs where each input is related to exactly one output.
instantaneous acceleration: The instantaneous change in velocity in an infinitely small time period.
integral: The area of the region in a plane bounded by the graph of a function and the x-axis. It is the inverse of a derivative and is sometimes called an antiderivative.
velocity: The rate of change in the displacement of an object. Velocity is a vector and has two components: speed and direction.
Assessment
Pre-Lesson Assessment
Use the questions presented in the Introduction/Motivation (also listed below) to generate a class discussion or as a formative assessment of each student's knowledge of the concept of acceleration.
- What will be the motion of the device? Describe this motion. (Answer: The device should speed up when it is first released and then slow down until it comes to a stop.)
- Will the acceleration of the device be constant? What about the force acting on the device? (Answer: The acceleration will not be constant since the device will speed up then slow down. Since the rubber band will not maintain the same "stretch," the force on the object will not be constant. This means that the acceleration will change over time.)
- Will the velocity of the device ever be negative? (Answer: The device will travel in one direction only, so the velocity will always be either positive or always negative depending on which direction we call positive. However integration could result in negative velocity when only positive velocity is expected. Students need to be aware of this.)
- Will the acceleration of the device ever be negative? (Answer: Yes. Since the device will both speed up and slow down, it will have both positive and negative acceleration, no matter how we orient the directions.)
- What would an acceleration vs. time graph look like for this demonstration? (Answer: The graph should resemble one period of a sinusoidal graph, with a maximum followed by a minimum or the graph will appear similar to the function, f(x)=(-bx)/(x2+1), translated to the right where b is a scale factor.)
Summative Assessment
Assign students to provide answers and justifications for the questions and problems on the Android Acceleration Assessment. Answers are provided on the Android Acceleration Assessment Answer Key. Through this assessment, students demonstrate their understanding of acceleration both conceptually and mathematically. Their comprehension of the first three questions is critical for their performance in the associated activity. Review student answers to these questions to make sure all students understand the concepts.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students observe four different classroom setups with objects in motion (using toy cars, a ball on an incline, and a dynamics cart). At the first observation of each scenario, students sketch predicted position vs. time and velocity vs. time graphs.

Students are introduced to the concepts of force, inertia and Newton's first law of motion: objects at rest stay at rest and objects in motion stay in motion unless acted upon by an unbalanced force. Students learn the difference between speed, velocity and acceleration, and come to see that the cha...

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Students explore motion, rockets and rocket motion while assisting Spacewoman Tess, Spaceman Rohan and Maya in their explorations. First they learn some basic facts about vehicles, rockets and why we use them. Then, they discover that the motion of all objects—including the flight of a rocket and mo...
Copyright
© 2013 by Regents of the University of Colorado; original © 2012 Board of Regents, University of NebraskaContributors
Scott Burns, Brian SandallSupporting Program
IMPART RET Program, College of Information Science & Technology, University of Nebraska-OmahaAcknowledgements
The contents of this digital library curriculum were developed as a part of the RET in Engineering and Computer Science Site on Infusing Mobile Platform Applied Research into Teaching (IMPART) Program at the University of Nebraska-Omaha under National Science Foundation RET grant number CNS 1201136. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: September 11, 2020









User Comments & Tips