A Place in Space
The 3D coordinate system.
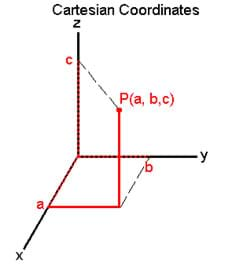
Student groups use a "real" 3D coordinate system to plot points in space. Made from balsa wood or wooden dowels, the system has three axes at right angles and a plane (the XY plane) that can slide up and down the Z axis. Students are given several coordinates and asked to find these points in space. Then they find the coordinates of the eight corners of a box/cube with given dimensions.
Engineers use a coordinate system whenever they create engineering drawings of objects and structures, and the Cartesian coordinate system modeled in this activity is used most often.
After this activity, students shold be able to:
- Locate a point in space, given its coordinates and an origin.
- Describe the location of a given point in space relative to some origin using coordinates.
- CCSS.Math.Content.6.NS.C.6c Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
Grade 6
Do you agree with this alignment? - CCSS.Math.Content.6.NS.C.8 Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.
Grade 6
Do you agree with this alignment? - CCSS.Math.Content.7.G.B.6 Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Grade 7
Do you agree with this alignment? - CCSS.Math.Content.HSG-CO.D.12 Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
Grades 9-12
Do you agree with this alignment?
- Information and communication systems allow information to be transferred from human to human, human to machine, and machine to human.
Grades 6-8
Do you agree with this alignment? - The use of symbols, measurements, and drawings promotes a clear communication by providing a common language to express ideas.
Grades 6-8
Do you agree with this alignment?
- CCSS.Math.Content.6.NS.C.6c Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
Grade 6
Do you agree with this alignment? - CCSS.Math.Content.6.NS.C.8 Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.
Grade 6
Do you agree with this alignment? - CCSS.Math.Content.7.G.B.6 Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
Grade 7
Do you agree with this alignment? - CCSS.Math.Content.HSG-CO.D.12 Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
Grades 9-12
Do you agree with this alignment?
- 3-foot length of ¼ inch x ¼ inch balsa wood or wooden dowel
- a fast adhesive such as a hot glue gun, rubber cement or a golf ball-sized ball of clay
- marker
- ruler
- utility knife or scissors
- 1 inch x 1 inch square of corrugated cardboard, foamcore board or poster board
Minimal prior experience graphing in two dimensions is helpful, but not required.
The contents of the Introduction/Motivation section of 3-D Coordinate System to Map Galaxies: The Next Dimension associated lesson also serve as the introduction to this activity.
Before the Activity
Gather materials and make copies of the 3D Coordinaes Worksheet (PDF).
Follow these steps to build one set of axes for each group. Alternatively, have the groups build the axes themselves.
- Cut the balsa wood into three segments of 1 foot each. (This will likely take an extra 15-20 minutes.)
- Use a glue gun (or other adhesive or clay) to glue the three pieces together so that all three are perpendicular to each other, meeting at one point. This forms the three axes.
- Using a ruler and marker, make marks every inch on each of the three axes, moving away from the origin. Make a total of 10 marks on each axis. If desired, number the markings so that on each axis, "1" is closest to the origin, and "10" is farthest out on the axis.
- Using a utility knife or scissors, cut the cardboard, foam board or poster board into a 1 foot x 1 foot square. Make a small hole in one corner of the square, about a half inch in from the edges. Make the hole just big enough for the balsa wood axis to fit through.
- This foam board serves as the XY plane. Slide it over one of the axes (the Z axis) all the way down until it is resting on the other two axes. The hole where the Z axis slides through the XY plane is now at the origin.
- Use the ruler to draw a 10 inch x 10 inch grid on the plane. Space the grid every inch, so that they match up with the markings on the X and Y axes. Then label the axes on the plane "X" and "Y" and number from 1 to 10 (again counting up as you move away from the origin. These numbers should match up with the numbers on the X and Y balsa wood axes.
- You have now constructed a 3D coordinate system with a moveable XY plane. To locate a point, first find the desired X and Y coordinates on the XY plane (traditional 2D graphing) and then slide the entire plane up to the specified Z coordinate.
With the Students
- Divide the class into groups of three students each. Give each group a set of three axes.
- Hand out the worksheet, which guides students through the 3D activity.
- dimension
- A measure of special extent. What we see around us is a three-dimensional world, because objects have three dimensions: length, width and height. A line is in one dimension, an area (such as a rectangle drawn on a piece of paper) is in two dimensions, and a box (cube) has three dimensions.
- axis
- In math, a line used as a reference to describe the location of a point. For example, in the Cartesian coordinate system, an axis is a line marked zero at a certain point. An object's location can then be described by measuring how far away (on the line) it is from this origin, and in what direction. In many ways, an axis is like a number line that goes on forever in both directions (positive and negative). An axis is one dimensional.
- plane
- The set of all points between two intersecting lines. A plane is two dimensional, so it is a flat surface. A flat table top, for example, can be thought of as a plane.
- ordered pair
- Two numbers used to describe the location of a point within a plane, relative to a specified reference point. For example, if you are told that the front left corner of your desk is the origin, and you want to find a point given the ordered pair (2, 3) and you know that the unit you are using is inches, you start at that front left corner of your desk, move two inches to the right, and then 3 inches toward the back of the desk, and you find that point.
- graph
- A visual representation of a mathematical function or set of numbers. In the previous definition for ordered pair, if your desk surface is thought of as a graph, you graphed the point (2,3), meaning you represented those numbers visually (or graphically).
- origin
- The specified reference point [(0,0,0) in most coordinate systems]
- cartesian coordinate system
- The rectangular coordinate system developed by the famous mathematician Descartes. It consists of 2 or 3 axes (X, Y and Z) all at right angles to each other, and all intersecting at a specified origin.
Worksheet: If students are able to satisfactorily complete the 3D Coordinates Worksheet (PDF) with little or no help from the teacher or peers, then they demonstrate a sound understanding of the basics of 3D graphing.
- If students use utility knives to cut the cardboard or foamcore board, closely supervise them and watch for dangerous use of these sharp tools.
- Warn students that the glue guns and the glue get very hot. Also take care with other adhesives and follow their safety instructions
Have students find the points to describe shapes that are more complicated than a box.
Try drawing the 3D axes on a piece of paper. Then, try to draw a cube in 3D by locating points on the axes
Change the plane from the XY plane to the XZ or YZ planes by sliding it down a different axis. The points may be located in the same manner, and students will learn that the particular letters and orientation of the planes is arbitrary.
- Have less-advanced students do only the 2D part.
- To save time and cost, build just one set of 3D axes and present the activity as a class demonstration, instead of each group having its own set of axes.
Contributors
Ben Burnham
Supporting Program
Techtronics Program, Pratt School of Engineering, Duke University
Acknowledgements
This content was developed by the MUSIC (Math Understanding through Science Integrated with Curriculum) Program in the Pratt School of Engineering at Duke University under National Science Foundation GK-12 grant no. DGE 0338262. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Copyright
2013 by Regents of the University of Colorado; original © 2004 Duke University