Quick Look
Grade Level: 6 (5-7)
Time Required: 45 minutes
Allow an additional 15-20 minutes if students are asked to build their own sets of axes.
Lesson Dependency: None
Subject Areas: Geometry, Science and Technology
NGSS Performance Expectations:

| MS-ESS1-3 |

Summary
Sudents learn about the three-dimensional Cartesian coordinate system. They also gain perspective on the size of our galaxy (the Milky Way) and the distance of a nearby spiral galaxy, the Andromeda galaxy (shown on the left), using a 3D model. 3D graphing is an important tool used by structural engineers to describe locations in space to fellow engineers. A student worksheet with answer key is provided.Engineering Connection
Engineers use a coordinate system whenever they create engineering drawings of objects and structures. This lesson introduces the commonly used Cartesian coordinate system using A Place in Space activity.
Learning Objectives
At the end of the lesson, students shoud:
- Be able to find a point in space given the X, Y and Z coordinates.
- Have a sense for the dimensions of the Milky Way galaxy, where the Sun is in within it, and the distance to a nearby galaxy.
- Be able to give the X, Y and Z coordinates, given a point in space relative to a specified coordinate system and origin.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ESS1-3. Analyze and interpret data to determine scale properties of objects in the solar system. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Analyze and interpret data to determine similarities and differences in findings. Alignment agreement: | The solar system consists of the sun and a collection of objects, including planets, their moons, and asteroids that are held in orbit around the sun by its gravitational pull on them. Alignment agreement: | Time, space, and energy phenomena can be observed at various scales using models to study systems that are too large or too small. Alignment agreement: Engineering advances have led to important discoveries in virtually every field of science, and scientific discoveries have led to the development of entire industries and engineered systems.Alignment agreement: |
Common Core State Standards - Math
-
Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates. Understand that the first number indicates how far to travel from the origin in the direction of one axis, and the second number indicates how far to travel in the direction of the second axis, with the convention that the names of the two axes and the coordinates correspond (e.g., x-axis and x-coordinate, y-axis and y-coordinate).
(Grade
5)
More Details
Do you agree with this alignment?
-
Understand signs of numbers in ordered pairs as indicating locations in quadrants of the coordinate plane; recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
(Grade
6)
More Details
Do you agree with this alignment?
-
Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
(Grade
7)
More Details
Do you agree with this alignment?
-
Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Information and communication systems allow information to be transferred from human to human, human to machine, and machine to human.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
The use of symbols, measurements, and drawings promotes a clear communication by providing a common language to express ideas.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
North Carolina - Math
-
Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates. Understand that the first number indicates how far to travel from the origin in the direction of one axis, and the second number indicates how far to travel in the direction of the second axis, with the convention that the names of the two axes and the coordinates correspond (e.g., x-axis and x-coordinate, y-axis and y-coordinate).
(Grade
5)
More Details
Do you agree with this alignment?
-
Understand signs of numbers in ordered pairs as indicating locations in quadrants of the coordinate plane; recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
(Grade
6)
More Details
Do you agree with this alignment?
-
Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
(Grade
7)
More Details
Do you agree with this alignment?
-
Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/duk_dimension_tech_less] to print or download.Pre-Req Knowledge
Some experience with the two-dimensional Cartesian coordinate system is helpful, but is not required.
Introduction/Motivation
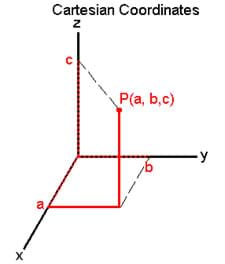
Use a flat surface such as a piece of paper, or a table top. Put your finger at a point on the surface, and ask students how they would describe the location of that point. If they have had experience graphing on the XY plane, they will probably figure out that they can give the coordinates of that point relative to a particular corner (over 5 inches, up 9 inches). If they do not get this on their own, ask leading questions to help them. For example, "Well how far away is the point from the side of the paper?" Once students grasp this, move your finger so that it is above the surface you are using. Then ask them again how they would describe the location of that point. They may say something like "above the paper." Ask them to be more specific. The goal is to get them to give a description such as "5 inches over from the left side, 9 inches up, and 6 inches above." Ask them to give you the three coordinates necessary to describe the location of the points.
Next, spend a short time discussing the terms in the vocabulary section.
It is helpful to describe some concrete examples of how the 3D coordinate system is used in everyday life. For example, when you describe the location of an office within a building, you are essentially using coordinates: "Go up 3 floors, do down the hall past four doors and turn right, it's the second room on your left." City blocks are another example of the use of a coordinate system. Directions from one house to another might read, "Go three blocks, then take a right and go four blocks." This is an example of a two-dimensional coordinate system.
Coordinate systems can also help us visualize where we are within our galaxy, as well as how far away a "nearby" galaxy is in space. Have students complete the Galactic Perspectives Worksheet. Students should be placed in teams of 2-3 and each team should be given a ruler.
Lesson Background and Concepts for Teachers
The purpose of this lesson is to familiarize students with 2D and 3D graphing and to use these tools to develop a sense of the spatial scales relevant to our galaxy including its spatial dimensions and relative distances between objects within the Milky Way and a neighboring galaxy. Have students complete the worksheet to achieve this goal.
Students can also learn the basics of graphing in three dimensions. Conduct the A Place in Space associated activity to accomplish this. Its worksheet guides students to first review finding points on the 2D (XY) plane, and then moves on to finding and describing points in a 3D space (X, Y ,Z). In order to get the most out of the activity, groups need their own set of axes. Instructions for how to build these as well as supplies needed are described in the activity's Procedure section.
Associated Activities
- A Place in Space - Students practice finding points in space and then describing the locations of given points in space.
Lesson Closure
Coordinate systems can be used for more than mapping objects in space. A coordinate system is used by engineers in all designs. The coordinate system is used to specify dimensions for products. When an engineer designs a part, s/he specifies where each point on the part is located using a Computer Aided Design (CAD) program. Often, parts can be manufactured by sending a CAD drawing file to a machine that is designed to interpret the file and create the part.
- We have learned how to locate a point given an origin, and the X, Y and Z coordinates.
- We can also describe the location of a point by providing this information.
- We have applied this information to construct a 3-D model of our galaxy and a neighboring galaxy, and have gained some insight into galactic distances and related spatial scales.
Vocabulary/Definitions
axis: In math, a line used as a reference to describe the location of a point. For example, in the Cartesian coordinate system, an axis is a line marked zero at a certain point. An object's location can then be described by measuring how far away (on the line) it is from this origin, and in what direction. In many ways, an axis is like a number line that goes on forever in both directions (positive and negative). An axis is one dimensional.
Cartesian coordinate system: The rectangular coordinate system developed by mathematician Descartes. It consists of 2 or 3 axes (X, Y and Z) all at right angles to each other, and all intersecting at a specified origin.
dimension: A measure of spatial extent. What we see around us is a three-dimensional world, because objects have three dimensions (length, width and height). A line is in one dimension, an area (such as a rectangle drawn on a piece of paper) is in two dimensions, and a box has three dimensions.
Galactic center: The center of the Milky Way galaxy
graph: A visual representation of a mathematical function or set of numbers. In the previous definition for ordered pair, if your desk surface could be thought of as a graph, and you graphed the point (2,3), this means you represented those numbers visually (or graphically).
ordered pair: A way to describe the location of a point within a plane, relative to a specified reference point. For example, if the front left corner of your desk is the origin, and you want to find a point given the ordered pair (2, 3) and you know that the unit you are using is inches, you would start at that front left corner of your desk, move two inches to the right, and then 3 inches toward the back of the desk, and you would be at that point.
origin: The specified reference point (0,0,0) in most coordinate systems.
plane: The set of all points between two intersecting lines. A plane is two dimensional, so it is a flat surface. A flat table top, for example, can be thought of as a plane.
Assessment
- If students were able to satisfactorily complete the Galactic Perspectives Worksheet with little or no help from teachers or peers then they have demonstrated the ability to use 2-D and 3-D models to explore the spatial scales and dimensions of the Milky Way galaxy and the relative distance to the nearest spiral galaxy (the Andromeda galaxy).
- If students were able to satisfactorily complete the A Place in Space activity worksheet with little or no help from teachers or peers then they have demonstrated a sound understanding of the basics of plotting coordinates in three dimensions.
- Students should be able to locate a point in space, given its coordinates and an origin.
- Students should be able to describe the location of a given point in space relative to some origin using coordinates.
- Should have an enhanced perspective on the dimensions of our galaxy and appreciate the relative distance to other nearby galaxies
Lesson Extension Activities
A practical way to apply what students have learned in this lesson/activity is to have them design basic structures such as bridges or towers using a computer aided design (CAD) program.
Students could also calculate the scaled-distances to much farther away galaxies, and discover that these galaxies would be quite far away even using the scale model that was applied to the Milky Way.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn about linear programming (also called linear optimization) to solve engineering design problems. They apply this information to solve two practice engineering design problems related to optimizing materials and cost by graphing inequalities, determining coordinates and equations from ...

Student groups use a "real" 3D coordinate system to plot points in space. Made from balsa wood or wooden dowels, the system has three axes at right angles and a plane (the XY plane) that can slide up and down the Z axis.

Students learn about projections and coordinates in the geographic sciences that help us to better understand the nature of the Earth and how to describe location.

A brief refresher on the Cartesian plane includes how points are written in (x, y) format and oriented to the axes, and which directions are positive and negative. Then students learn about what it means for a relation to be a function and how to determine domain and range of a set of data points.
Copyright
© 2013 by Regents of the University of Colorado; original © 2004 Duke UniversityContributors
Ben BurnhamSupporting Program
Techtronics Program, Pratt School of Engineering, Duke UniversityAcknowledgements
This content was developed by the MUSIC (Math Understanding through Science Integrated with Curriculum) Program in the Pratt School of Engineering at Duke University under National Science Foundation GK-12 grant no. DGE 0338262. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: April 5, 2019









User Comments & Tips